3.1.3 黄金分割 课件 (共12页)
文档属性
| 名称 | 3.1.3 黄金分割 课件 (共12页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 07:03:58 | ||
图片预览




文档简介
(共12张PPT)
3.1.3 黄金分割
湘教版九年级上册
情境导入
(1)有经验的主持人一般站在舞台上的哪个位置?是正中央吗?
说一说
(2)人为什么在环境气温22℃~24℃下感到最适宜?
合作探究
1、黄金分割
动脑筋
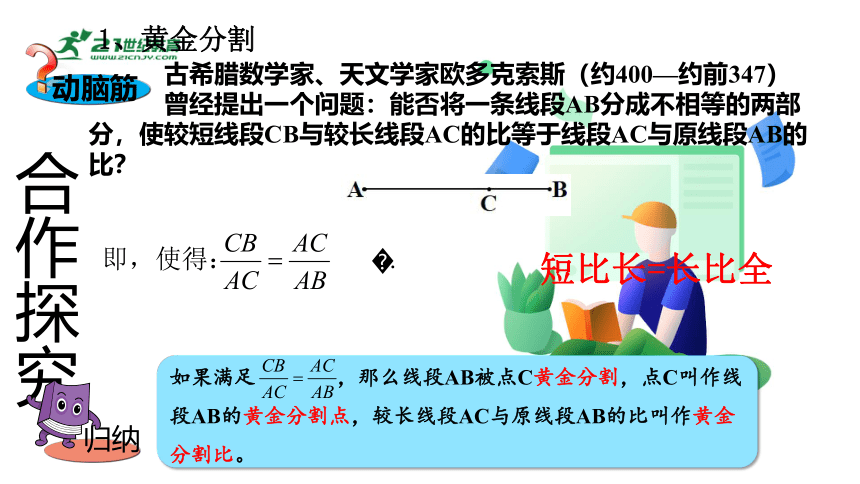
古希腊数学家、天文学家欧多克索斯(约400—约前347)
曾经提出一个问题:能否将一条线段AB分成不相等的两部分,使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比?
短比长=长比全
如果满足 ,那么线段AB被点C黄金分割,点C叫作线段AB的黄金分割点,较长线段AC与原线段AB的比叫作黄金分割比。
归纳
合作探究
1、黄金分割
动脑筋
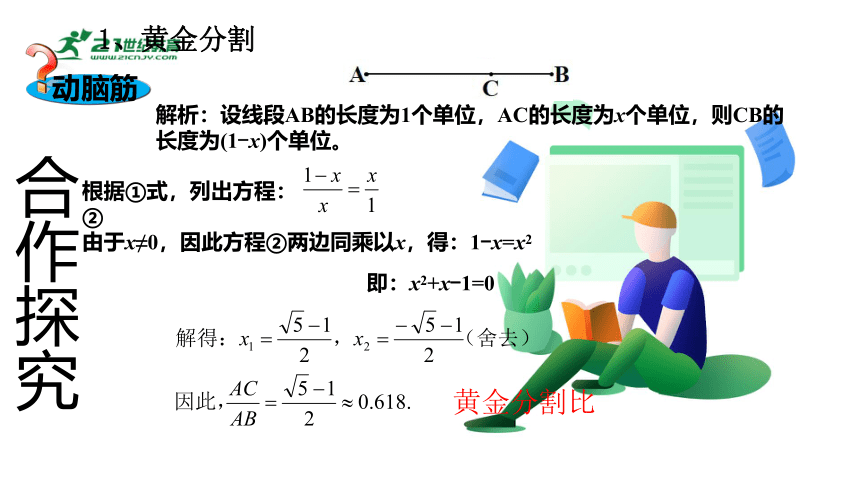
解析:设线段AB的长度为1个单位,AC的长度为x个单位,则CB的长度为(1-x)个单位。
根据①式,列出方程: ②
由于x≠0,因此方程②两边同乘以x,得:1-x=x2
即:x2+x-1=0
黄金分割比
课堂练习
做一做
D
1、已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),
则下列结论中正确的是( )
A. B. C. D.
2、如图,以长为2的线段AB为边,作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取一点F,使PF=PD。求证:点A是线段BF的黄金分割点。
合作探究
2、黄金分割点的几何作图
动脑筋
我们知道任意线段都有黄金分割点,那如何找到它呢?
给定一条线段AB,找出它的黄金分割点。作法如下:
(2)连接AC,以点C为圆心,CB为半径画弧,交AC于点E;
(3)以点A为圆心,AE为半径画弧,交AB 于点P。
则点P为所求作的线段AB的黄金分割点。
(1)过点B作AB的垂线,并在垂线上取BC= AB;
合作探究
3、介绍黄金分割的现实生活的应用
说一说
1、在“中华经典美文阅读”活动中,小明同学发现自己
的一本书的宽与长之比为黄金分割比。已知这本书的长为20cm,则宽约为 cm(精确到0.1cm);
2、已知线段AB=2cm,点C在线段AB上,且AC2=BC AB,则AC的长为 cm;
3、线段a,b,c满足a︰b=3︰2,且b是a,c的比例中项,那么b︰c等于( )
A. 4︰3 B. 3︰4 C. 2︰3 D. 3︰2
课堂练习
练习
12.4
D
课堂小结
通过本节课的学习,你有什么收获与体会?
1. 甲、乙两地的实际距离为680km,在某地图上量得这两地的距离为17cm,求该地图的比例尺.
作业设计
练习
1︰4 000 000
2. 节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体. 若舞台AB长为20m,则主持人站在离A点多远处最自然得体?(结果精确到0.1m)
离A点12.4m或7.6m.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.1.3 黄金分割
湘教版九年级上册
情境导入
(1)有经验的主持人一般站在舞台上的哪个位置?是正中央吗?
说一说
(2)人为什么在环境气温22℃~24℃下感到最适宜?
合作探究
1、黄金分割
动脑筋
古希腊数学家、天文学家欧多克索斯(约400—约前347)
曾经提出一个问题:能否将一条线段AB分成不相等的两部分,使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比?
短比长=长比全
如果满足 ,那么线段AB被点C黄金分割,点C叫作线段AB的黄金分割点,较长线段AC与原线段AB的比叫作黄金分割比。
归纳
合作探究
1、黄金分割
动脑筋
解析:设线段AB的长度为1个单位,AC的长度为x个单位,则CB的长度为(1-x)个单位。
根据①式,列出方程: ②
由于x≠0,因此方程②两边同乘以x,得:1-x=x2
即:x2+x-1=0
黄金分割比
课堂练习
做一做
D
1、已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),
则下列结论中正确的是( )
A. B. C. D.
2、如图,以长为2的线段AB为边,作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取一点F,使PF=PD。求证:点A是线段BF的黄金分割点。
合作探究
2、黄金分割点的几何作图
动脑筋
我们知道任意线段都有黄金分割点,那如何找到它呢?
给定一条线段AB,找出它的黄金分割点。作法如下:
(2)连接AC,以点C为圆心,CB为半径画弧,交AC于点E;
(3)以点A为圆心,AE为半径画弧,交AB 于点P。
则点P为所求作的线段AB的黄金分割点。
(1)过点B作AB的垂线,并在垂线上取BC= AB;
合作探究
3、介绍黄金分割的现实生活的应用
说一说
1、在“中华经典美文阅读”活动中,小明同学发现自己
的一本书的宽与长之比为黄金分割比。已知这本书的长为20cm,则宽约为 cm(精确到0.1cm);
2、已知线段AB=2cm,点C在线段AB上,且AC2=BC AB,则AC的长为 cm;
3、线段a,b,c满足a︰b=3︰2,且b是a,c的比例中项,那么b︰c等于( )
A. 4︰3 B. 3︰4 C. 2︰3 D. 3︰2
课堂练习
练习
12.4
D
课堂小结
通过本节课的学习,你有什么收获与体会?
1. 甲、乙两地的实际距离为680km,在某地图上量得这两地的距离为17cm,求该地图的比例尺.
作业设计
练习
1︰4 000 000
2. 节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体. 若舞台AB长为20m,则主持人站在离A点多远处最自然得体?(结果精确到0.1m)
离A点12.4m或7.6m.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
