16。3分式方程2[下学期]
文档属性
| 名称 | 16。3分式方程2[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-26 23:07:00 | ||
图片预览








文档简介
课件23张PPT。16.3分式方程2浙江省玉环实验学校 徐课前热身2、在行程问题中,主要是有三个量:路程、速度、时间。它们的关系是:
路程= 、速度= 、时间= 。 3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。1、解分式方程 一个“必须”是:必须 ;
二个“基本”是:解分式方程的基本思想是 ,基本方法是 ;三个“步骤”是: ,
, 。转化去分母去分母解整式方程检验检验速度×时间静水速度 + 水流速度静水速度-水流速度解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,
依题意得:汽车所用的时间=自行车所用时间- 时即:15=45-2x x=15检验:x=15时,3x≠0,x=15是原方程的根由x=15得3x=45答:自行车的速度是15千米/时,汽车的速度是45千米/时.得到结果记住要检验。例1:农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度。方法1:方法2:解:设汽车从出发到追上骑车同学的时间为x小时,
依题意得:答:自行车的速度是15千米/时,汽车的速度是45千米/时.根据速度关系 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
例2: 某班学生到距学校12千米的烈士陵园扫墓,一部分人骑自行车先行,经0.5时后,其余的人乘汽车出发,结果他们同时到达.已知汽车的速度是自行车的3倍,求自行车和汽车的速度.解:设自行车速度为x千米/时,则汽车速度为________千米/时3x 解得:x=16
经检验: x=16是原方程的根;
3x=48
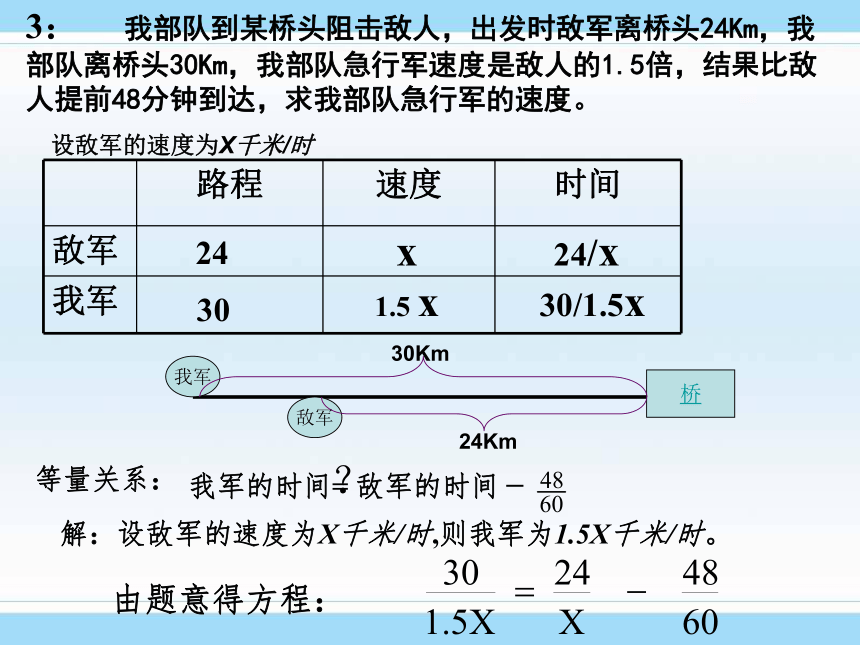
答:自行车速度是16千米/时,汽车速度是48千米/时,3: 我部队到某桥头阻击敌人,出发时敌军离桥头24Km,我部队离桥头30Km,我部队急行军速度是敌人的1.5倍,结果比敌人提前48分钟到达,求我部队急行军的速度。 等量关系: 我军的时间= 敌军的时间 解:设敌军的速度为X千米/时,则我军为1.5X千米/时。 由题意得方程: 24 30x1.5 x24/x30/1.5x?–设敌军的速度为X千米/时桥敌军我军24Km30Km4:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快。分析:甲队1个月完成总工程的 ,设乙队如果
单独施工1个月完成总工程的 ,那么甲队
半个月完成总工程的_____,乙队半个月完
成总工程的_____,两队半个月完成总工程
的_______.
解:设乙队如果单独施工1个月完成总工程的 .
依题意得方程两边同乘6x,得
2X+X+3=6X
解得 x=1
检验:x=1时6x≠0,x=1是原分式方程的解
由上可知,若乙队如果单独施工1个月可以完成全部任务,甲队1个月完成总工程的 ,可知乙队施工速度快. 重庆市政府打算把一块荒地建成公园,动用了一台甲型挖土机,4天挖完了这块地的一半。后又加一台乙型挖土机,两台挖土机一起挖,结果1天就挖完了这块地的另一半。乙型挖土机单独挖这块地需要几天?(1)设乙型挖土机单独挖这块地需要x天,那么它1天挖土量是
这块地的_______;
分析:请完成下列填空:(2)甲型挖土机1天挖土量是
这块地的______;(3)两台挖土机合挖,1天挖土
量是这块地的_____.随堂练习1.一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
练习:某工程队需要在规定日期内完成。若甲队单独做
正好按时完成;若乙队单独做,超过规定日期三天
才能完成。现由甲、乙合作两天,余下工程由乙队
单独做,恰好按期完成,问规定日期是多少天?解;设规定日期是x天,根据题意,得:方程两边同乘以x(x+3),得:2(x+3)+x2=x(x+3)解得: x=6检验:x=6时x(x+3)≠0,x=6是原方程的解。答:规定日期是6天。2、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?3:某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?解:设原计划每天挖x米,则实际每天挖___________米。x(1+50%)每天比计划多挖50%4、在我市某桥的维修工程中,拟由甲、乙两个工程队共同完成某项目.从两个工程队的资料可以知道:若两个工程队合做24天恰好完成;若两工程队合做18天后,甲工程队再单独做10天,也恰好完成,请问:
(1)甲、乙两个工程队单独完成该项目各需多少天?(2)又已知甲工程队每天的施工费为0.6万元,乙工程队每天的施工费为0.35万元,要使该项目总的施工费不超过22万元,则乙施工队最少施工多少天?例5、小王在超市用了24元钱买了某种品牌的牛奶若干盒,过了一段时间再去超市,发现这种牛奶进行让利销售,每盒让利0.4元,他同样用了24元钱买,比上次多买了2盒,求他第一次买了多少盒这种牛奶。解:设他第一次买了x盒这种牛奶,则第二次买了______盒。(x+2)5..某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,
求该市今年居民用水的价格?
解:设该市去年用水的价格为x元/吨.解得 x=1.5
经检验x=1.5是原方程的根.
1.5×4/3=2(元)
答:该市今年居民用水的价格为2元/吨 6.某地电话公司调低了长途电话的话费标准,每分钟费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟.问前后两种收费标准每分钟收费各是多少? 长话费调 低了? 分析:若设原来的收费标准是x元/分,则可列出方程: 7.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求两年每间出租房屋的租金?
(2)求出租房屋的总间数?练习解法1:设共有x间出租房.解法2:设第一年每间房屋的租金为x元.某商厦进货员预测一种应季衬衫能畅销市场,就用2万元购进这种衬衫,面市后果然供不应求,商厦又用4.3万元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了3元;要知道共赢利多少,须知共卖出多少服装解:设第一批服装为x件,则第二批为2x件解得x=500经检验: x=500是方程的根
∴ 2x=100089400-(20000+43000)=23400(元)商厦销售这种衬衫时每件定价都是60元,最后剩下的50件按八折销售,很快售完,在这两笔生意中,商厦共赢利多少元?答:商厦共赢利23400元。本题还可以设第一次的服装单价为x元,第二次的为(x+4)元,列出另一个分式方程求解,回去试试看!再 见
路程= 、速度= 、时间= 。 3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。1、解分式方程 一个“必须”是:必须 ;
二个“基本”是:解分式方程的基本思想是 ,基本方法是 ;三个“步骤”是: ,
, 。转化去分母去分母解整式方程检验检验速度×时间静水速度 + 水流速度静水速度-水流速度解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,
依题意得:汽车所用的时间=自行车所用时间- 时即:15=45-2x x=15检验:x=15时,3x≠0,x=15是原方程的根由x=15得3x=45答:自行车的速度是15千米/时,汽车的速度是45千米/时.得到结果记住要检验。例1:农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度。方法1:方法2:解:设汽车从出发到追上骑车同学的时间为x小时,
依题意得:答:自行车的速度是15千米/时,汽车的速度是45千米/时.根据速度关系 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
例2: 某班学生到距学校12千米的烈士陵园扫墓,一部分人骑自行车先行,经0.5时后,其余的人乘汽车出发,结果他们同时到达.已知汽车的速度是自行车的3倍,求自行车和汽车的速度.解:设自行车速度为x千米/时,则汽车速度为________千米/时3x 解得:x=16
经检验: x=16是原方程的根;
3x=48
答:自行车速度是16千米/时,汽车速度是48千米/时,3: 我部队到某桥头阻击敌人,出发时敌军离桥头24Km,我部队离桥头30Km,我部队急行军速度是敌人的1.5倍,结果比敌人提前48分钟到达,求我部队急行军的速度。 等量关系: 我军的时间= 敌军的时间 解:设敌军的速度为X千米/时,则我军为1.5X千米/时。 由题意得方程: 24 30x1.5 x24/x30/1.5x?–设敌军的速度为X千米/时桥敌军我军24Km30Km4:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快。分析:甲队1个月完成总工程的 ,设乙队如果
单独施工1个月完成总工程的 ,那么甲队
半个月完成总工程的_____,乙队半个月完
成总工程的_____,两队半个月完成总工程
的_______.
解:设乙队如果单独施工1个月完成总工程的 .
依题意得方程两边同乘6x,得
2X+X+3=6X
解得 x=1
检验:x=1时6x≠0,x=1是原分式方程的解
由上可知,若乙队如果单独施工1个月可以完成全部任务,甲队1个月完成总工程的 ,可知乙队施工速度快. 重庆市政府打算把一块荒地建成公园,动用了一台甲型挖土机,4天挖完了这块地的一半。后又加一台乙型挖土机,两台挖土机一起挖,结果1天就挖完了这块地的另一半。乙型挖土机单独挖这块地需要几天?(1)设乙型挖土机单独挖这块地需要x天,那么它1天挖土量是
这块地的_______;
分析:请完成下列填空:(2)甲型挖土机1天挖土量是
这块地的______;(3)两台挖土机合挖,1天挖土
量是这块地的_____.随堂练习1.一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
练习:某工程队需要在规定日期内完成。若甲队单独做
正好按时完成;若乙队单独做,超过规定日期三天
才能完成。现由甲、乙合作两天,余下工程由乙队
单独做,恰好按期完成,问规定日期是多少天?解;设规定日期是x天,根据题意,得:方程两边同乘以x(x+3),得:2(x+3)+x2=x(x+3)解得: x=6检验:x=6时x(x+3)≠0,x=6是原方程的解。答:规定日期是6天。2、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?3:某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?解:设原计划每天挖x米,则实际每天挖___________米。x(1+50%)每天比计划多挖50%4、在我市某桥的维修工程中,拟由甲、乙两个工程队共同完成某项目.从两个工程队的资料可以知道:若两个工程队合做24天恰好完成;若两工程队合做18天后,甲工程队再单独做10天,也恰好完成,请问:
(1)甲、乙两个工程队单独完成该项目各需多少天?(2)又已知甲工程队每天的施工费为0.6万元,乙工程队每天的施工费为0.35万元,要使该项目总的施工费不超过22万元,则乙施工队最少施工多少天?例5、小王在超市用了24元钱买了某种品牌的牛奶若干盒,过了一段时间再去超市,发现这种牛奶进行让利销售,每盒让利0.4元,他同样用了24元钱买,比上次多买了2盒,求他第一次买了多少盒这种牛奶。解:设他第一次买了x盒这种牛奶,则第二次买了______盒。(x+2)5..某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,
求该市今年居民用水的价格?
解:设该市去年用水的价格为x元/吨.解得 x=1.5
经检验x=1.5是原方程的根.
1.5×4/3=2(元)
答:该市今年居民用水的价格为2元/吨 6.某地电话公司调低了长途电话的话费标准,每分钟费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟.问前后两种收费标准每分钟收费各是多少? 长话费调 低了? 分析:若设原来的收费标准是x元/分,则可列出方程: 7.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求两年每间出租房屋的租金?
(2)求出租房屋的总间数?练习解法1:设共有x间出租房.解法2:设第一年每间房屋的租金为x元.某商厦进货员预测一种应季衬衫能畅销市场,就用2万元购进这种衬衫,面市后果然供不应求,商厦又用4.3万元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了3元;要知道共赢利多少,须知共卖出多少服装解:设第一批服装为x件,则第二批为2x件解得x=500经检验: x=500是方程的根
∴ 2x=100089400-(20000+43000)=23400(元)商厦销售这种衬衫时每件定价都是60元,最后剩下的50件按八折销售,很快售完,在这两笔生意中,商厦共赢利多少元?答:商厦共赢利23400元。本题还可以设第一次的服装单价为x元,第二次的为(x+4)元,列出另一个分式方程求解,回去试试看!再 见
