16.3分式方程的应用[下学期]
文档属性
| 名称 | 16.3分式方程的应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 965.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-03 08:51:00 | ||
图片预览








文档简介
课件29张PPT。分式方程的应用(1)16.3 分式方程解分式方程:
(1)
(2)
(3)问题 一辆快客车和一辆中巴车在公路上行驶,已知快客车每小时比中巴车多行20千米,快客车行驶80千米所需要的时间与中巴车行驶60千米所需要的时间相同,求快客车的速度.解: 设快客车每小时行驶X千米,则中巴车每小时行驶(X-20)千米,根据题意可得方程: 解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,
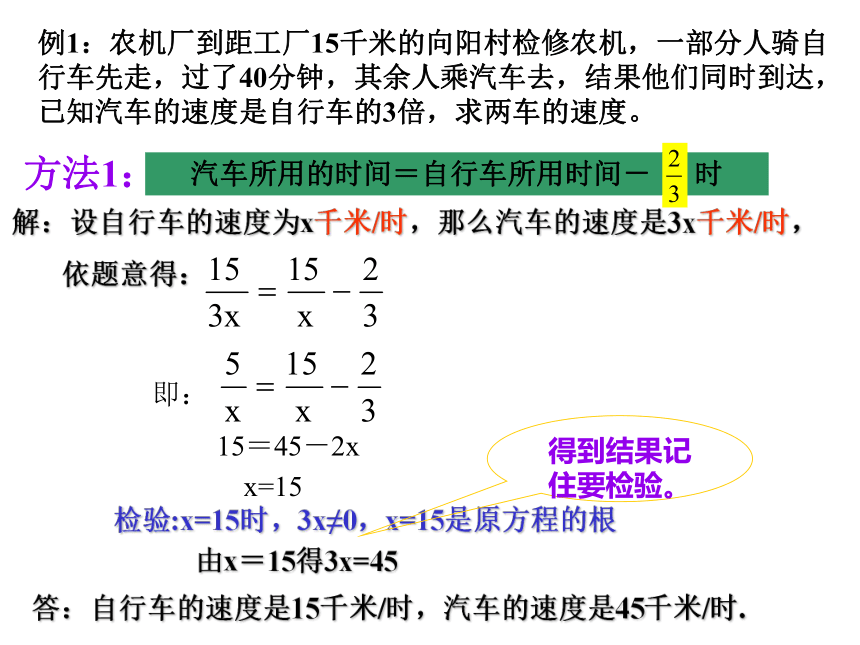
依题意得:汽车所用的时间=自行车所用时间- 时即:15=45-2x x=15检验:x=15时,3x≠0,x=15是原方程的根由x=15得3x=45答:自行车的速度是15千米/时,汽车的速度是45千米/时.得到结果记住要检验。例1:农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度。方法1:汽车的速度=3 自行车速度方法2:解:设汽车从出发到追上骑车同学的时间为x小时,
依题意得:当 时,解得:x=答:自行车的速度是15千米/时,汽车的速度是45千米/时.汽车的速度=3 自行车的速度根据速度关系经检验:x= 是原方程的根 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
某地电话公司调低了长途电话的话费标准,每分钟费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟.问前后两种收费标准每分钟收费各是多少? 长话费调 低了? 分析:若设原来的收费标准是x元/分,则可列出方程:自主学习甲、乙两地相距100千米,一辆长途客车从甲地开出2小时后,一辆轿车也从甲地开出,结果轿车比客车迟20分钟到达乙地。已知轿车和客车的速度的比是3 :2.求轿车和客车的速度?做一做:练习1.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求这两年每间出租房屋的租金?
(2)求出租房屋的总间数?
练一练:练习2.某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?练习3:某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?解:设原计划每天挖x米,则实际每天挖___________米。x(1+50%)工作效率比计划提高50%每天比计划多挖50%练习4.一艘轮船逆流航行2km的时间比顺流航行2 km的时间多用了40分钟, . (在横线上补充一个条件并提出一个问题) 已知水速为2 km/h求船在静水中的速度?如:条件:已知水速为2 km/h, 问题:求船在静水中的速度?解:设船在静水中的速度为x km/h.编写一道与下面分式方程相符的实际问题.你,我,他——人人都有创造力. 相信自己是最棒的.分式方程的应用(2)16.3 分式方程问题3两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快。分析:甲队1个月完成总工程的 ,设乙队如果
单独施工1个月完成总工程的 ,那么甲队
半个月完成总工程的_____,乙队半个月完
成总工程的_____,两队半个月完成总工程
的_______.
解:设乙队如果单独施工1个月完成总工程的 .
依题意得方程两边同乘6x,得
2X+X+3=6X
解得 x=1
检验:x=1时6x≠0,x=1是原分式方程的解
由上可知,若乙队如果单独施工1个月可以完成全部任务,甲队1个月完成总工程的 ,可知乙队施工速度快.随堂练习1、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
2、解一组方程,先用小计算器解20
分钟,再改用大计算器解25分钟可解完,如果大计算器的运算速度是小计算器的4倍,问用小计算器解这组方程需多少时间?3、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?4、在我市某桥的维修工程中,拟由甲、乙两个工程队共同完成某项目.从两个工程队的资料可以知道:若两个工程队合做24天恰好完成;若两工程队合做18天后,甲工程队再单独做10天,也恰好完成,请问:
(1)甲、乙两个工程队单独完成该项目各需多少天?(2)又已知甲工程队每天的施工费为0.6万元,乙工程队每天的施工费为0.35万元,要使该项目总的施工费不超过22万元,则乙施工队最少施工多少天?
学习是件很愉快的事,但又是一件很困难的事.困难是虎又是羊,看你是虎还是羊.你是绵羊它是虎, 你是老虎它是羊.再见!分式方程的应用(3)16.3 分式方程问题4从2004年5月起某列车平均提速v千米/时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?分析:设提速前列车的平均速度为x千米/时,
提速前列车行驶s千米所用的时间为___
小时,提速后列车的平均速度为_______
千米/时,提速后列车运行(s+50)千米所用
时间为______小时.
(x+v)列得方程:变式:当a为何值时,分式方程
会产生增根?例2:解关于x的分式方程例3照相机成像应用了重要的光学原理,即
。其中f表示照相机镜头的焦距,
u表示物体到镜头的距离,v表示胶片(像)
到镜头的距离。如果一架照相机f已固定,
那么就要依靠调整u,v,来使成像清晰。问
在已知f,v的情况下,怎样确定物体到镜头
的距离u?小结:本节课你有什么收获?作业:
(1)
(2)
(3)问题 一辆快客车和一辆中巴车在公路上行驶,已知快客车每小时比中巴车多行20千米,快客车行驶80千米所需要的时间与中巴车行驶60千米所需要的时间相同,求快客车的速度.解: 设快客车每小时行驶X千米,则中巴车每小时行驶(X-20)千米,根据题意可得方程: 解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,
依题意得:汽车所用的时间=自行车所用时间- 时即:15=45-2x x=15检验:x=15时,3x≠0,x=15是原方程的根由x=15得3x=45答:自行车的速度是15千米/时,汽车的速度是45千米/时.得到结果记住要检验。例1:农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度。方法1:汽车的速度=3 自行车速度方法2:解:设汽车从出发到追上骑车同学的时间为x小时,
依题意得:当 时,解得:x=答:自行车的速度是15千米/时,汽车的速度是45千米/时.汽车的速度=3 自行车的速度根据速度关系经检验:x= 是原方程的根 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
某地电话公司调低了长途电话的话费标准,每分钟费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟.问前后两种收费标准每分钟收费各是多少? 长话费调 低了? 分析:若设原来的收费标准是x元/分,则可列出方程:自主学习甲、乙两地相距100千米,一辆长途客车从甲地开出2小时后,一辆轿车也从甲地开出,结果轿车比客车迟20分钟到达乙地。已知轿车和客车的速度的比是3 :2.求轿车和客车的速度?做一做:练习1.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求这两年每间出租房屋的租金?
(2)求出租房屋的总间数?
练一练:练习2.某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?练习3:某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?解:设原计划每天挖x米,则实际每天挖___________米。x(1+50%)工作效率比计划提高50%每天比计划多挖50%练习4.一艘轮船逆流航行2km的时间比顺流航行2 km的时间多用了40分钟, . (在横线上补充一个条件并提出一个问题) 已知水速为2 km/h求船在静水中的速度?如:条件:已知水速为2 km/h, 问题:求船在静水中的速度?解:设船在静水中的速度为x km/h.编写一道与下面分式方程相符的实际问题.你,我,他——人人都有创造力. 相信自己是最棒的.分式方程的应用(2)16.3 分式方程问题3两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快。分析:甲队1个月完成总工程的 ,设乙队如果
单独施工1个月完成总工程的 ,那么甲队
半个月完成总工程的_____,乙队半个月完
成总工程的_____,两队半个月完成总工程
的_______.
解:设乙队如果单独施工1个月完成总工程的 .
依题意得方程两边同乘6x,得
2X+X+3=6X
解得 x=1
检验:x=1时6x≠0,x=1是原分式方程的解
由上可知,若乙队如果单独施工1个月可以完成全部任务,甲队1个月完成总工程的 ,可知乙队施工速度快.随堂练习1、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
2、解一组方程,先用小计算器解20
分钟,再改用大计算器解25分钟可解完,如果大计算器的运算速度是小计算器的4倍,问用小计算器解这组方程需多少时间?3、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?4、在我市某桥的维修工程中,拟由甲、乙两个工程队共同完成某项目.从两个工程队的资料可以知道:若两个工程队合做24天恰好完成;若两工程队合做18天后,甲工程队再单独做10天,也恰好完成,请问:
(1)甲、乙两个工程队单独完成该项目各需多少天?(2)又已知甲工程队每天的施工费为0.6万元,乙工程队每天的施工费为0.35万元,要使该项目总的施工费不超过22万元,则乙施工队最少施工多少天?
学习是件很愉快的事,但又是一件很困难的事.困难是虎又是羊,看你是虎还是羊.你是绵羊它是虎, 你是老虎它是羊.再见!分式方程的应用(3)16.3 分式方程问题4从2004年5月起某列车平均提速v千米/时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?分析:设提速前列车的平均速度为x千米/时,
提速前列车行驶s千米所用的时间为___
小时,提速后列车的平均速度为_______
千米/时,提速后列车运行(s+50)千米所用
时间为______小时.
(x+v)列得方程:变式:当a为何值时,分式方程
会产生增根?例2:解关于x的分式方程例3照相机成像应用了重要的光学原理,即
。其中f表示照相机镜头的焦距,
u表示物体到镜头的距离,v表示胶片(像)
到镜头的距离。如果一架照相机f已固定,
那么就要依靠调整u,v,来使成像清晰。问
在已知f,v的情况下,怎样确定物体到镜头
的距离u?小结:本节课你有什么收获?作业:
