1.8三角函数的简单应用 北师大版(2019)高中数学必修第二册(含答案解析)
文档属性
| 名称 | 1.8三角函数的简单应用 北师大版(2019)高中数学必修第二册(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 16:13:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.8三角函数的简单应用北师大版( 2019)高中数学必修第二册
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时秒.经过秒后,水斗旋转到点,设的坐标为,其纵坐标满足则下列叙述错误的是( )
A.
B. 当时,点到轴的距离的最大值为
C. 当时,函数单调递减
D. 当时,
如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为,转盘直径为,设置有个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要游客甲坐上摩天轮的座舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
一观览车的主架示意图如图所示,其中为轮轴的中心,距地面即长,巨轮的半径为,,巨轮逆时针旋转且每分钟转动一圈若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为,则( )
A. B.
C. D.
如图,重庆欢乐谷的摩天轮被称为“重庆之眼”,其旋转半径为米,最高点距离地面米,开启后按逆时针方向旋转,旋转一周大约分钟.将摩天轮看成圆面,在该平面内,以过摩天轮的圆心且垂直于地平面的直线为轴,该直线与地平面的交点为坐标原点建立平面直角坐标系,某人在最低点的位置坐上摩天轮的座舱,摩天轮开始启动,并记该时刻为,则此人距离地面的高度与摩天轮运行时间单位:分钟的函数关系式为( )
A. B.
C. D.
一个半径为米的水轮示意图,水轮的圆心距离水面米,已知水轮自点开始分钟逆时针旋转圈,水轮上的点到水面的距离单位:米与时间单位:秒满足函数关系式,,,则有( )
A. , B. ,
C. , D. ,
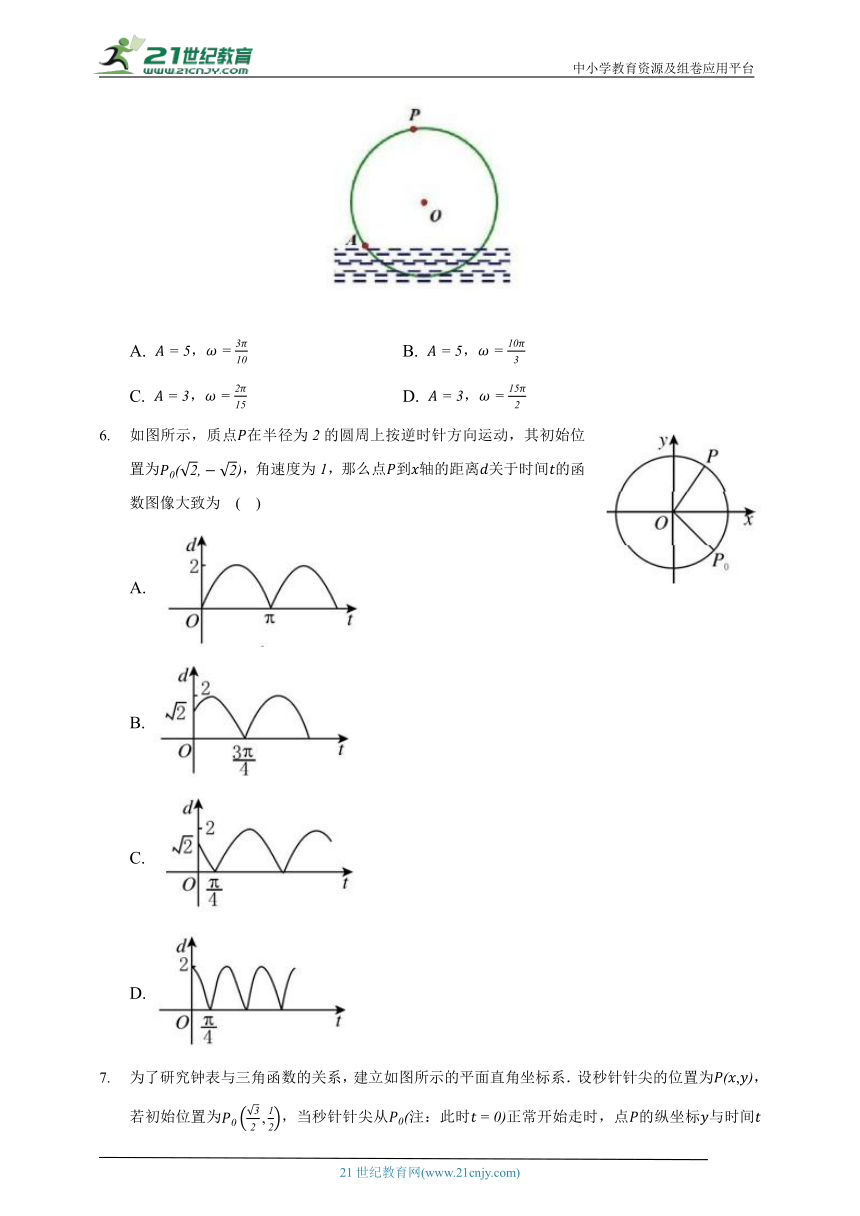
如图所示,质点在半径为的圆周上按逆时针方向运动,其初始位置为,角速度为,那么点到轴的距离关于时间的函数图像大致为 ( )
A.
B.
C.
D.
为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系.设秒针针尖的位置为,若初始位置为,当秒针针尖从注:此时正常开始走时,点的纵坐标与时间的函数关系式为.( )
A.
B.
C.
D.
一观览车的主架示意图如图所示,其中为轮轴的中心,距地面即长,巨轮的半径长为,,巨轮逆时针旋转且每分钟转一圈,若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为( )
A. B.
C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如下图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足则下列叙述正确的是( )
A.
B. 当时,函数单调递增
C. 当时,点到轴的距离的最大值为
D. 当时,
如图,摩天轮的半径为,其中心点距离地面的高度为,摩天轮按逆时针方向做匀速转动,且转一圈,若摩天轮上点的起始位置在最高点处,则摩天轮转动过程中( )
A. 经过点距离地面
B. 若摩天轮转速减半,则其周期变为原来的倍
C. 第和第时点距离地面的高度相同
D. 摩天轮转动一圈,点距离地面的高度不低于的时间为
水车在古代是进行灌溉引水的工具,亦称“水转简车”,是一种以水流作动力,取水灌田的工具.据史料记载,水车发明于隋而盛于唐,距今已有多年的历史,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足 ,则下列叙述正确的是
A.
B. 当时,函数单调递增
C. 当时,
D. 当时,的最大值为
一半径为米的水轮如图所示,水轮圆心距离水面米,已知水轮每秒逆时针转动一圈,如果当水轮上点从水中浮现时图中点开始计时,则( )
A. 点第一次到达最高点需要秒
B. 当水轮转动秒时,点距离水面米
C. 当水轮转动秒时,点在水面下方,距离水面米
D. 点距离水面的高度米与秒的函数解析式为
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
如图所示,一个大风车的半径为,每旋转一周,最低点离地面若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点离地面的距离与时间之间的函数关系是 .
年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是一个正方形和四个以正方形的边为底边、腰长为的等腰三角形组成的图形如图所示,为使占地面积最大,则等腰三角形的底角为 .
如下图所示,某公司计划建造一座滨海公园,直线与均为海岸沿线,是以为直角的直角三角形,线段为“滨海栈桥”,线段将建成“阳光沙滩沿线”,线段将建成“灯塔沿线”现要求“滨海栈桥”长度维持在不变的基础上,可适当调整“阳光沙滩沿线”与“灯塔沿线”的设计长度预计建成后,每“阳光沙滩沿线”可让公司日均盈利万元,每“灯塔沿线”可让公司日均盈利万元,为使公司日均盈利最大,则应将“灯塔沿线”设计为 .
如图所示,一个半径为米的筒车绕其轴心按逆时针方向匀速转动,每旋转周恰需要秒,轴心距水面的高度为米.设筒车上的某个盛水筒到水面的距离为单位:米,在水面下时为负数将盛水筒上浮到水面的一点设为起始位置,则与时间单位:秒之间的关系为,确定、、、的值,则 .
四、解答题(本大题共6小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
本小题分
游乐场中的摩天轮沿逆时针方向匀速旋转,其中心距离地面,半径示意图如下,游客从最低点处登上摩天轮,其与地面的距离随着时间而变化,已知游客将在登上摩天轮后分钟到达最高点,自其登上摩天轮的时刻起,
求出其与地面的距离与时间的函数关系的解析式;
若距离地面高度超过时,为“最佳观景时间”,那么在乘坐一圈摩天轮的过程中,该游客大约有多少“最佳观景时间”?
本小题分
如图所示,一个水轮的半径为,水轮圆心距离水面,已知水轮每分钟转动圈,如果当水轮上的点从水中浮现图中点时开始计算时间.
求动点距水面的高度单位:米与时间单位:秒的函数关系与满足正弦函数模型
在水轮的一圈转动中,求点露出水面的时长?
本小题分
如图,摩天轮的半径为,圆心距地面的高度为已知摩天轮按逆时针方向匀速转动,每转动一圈.游客在摩天轮的舱位转到距离地面最近的位置进舱.
游客进入摩天轮的舱位,开始转动后,他距离地面的高度为,求关于的函数解析式;
已知在距离地面超过的高度,游客可以观看到游乐场全景,那么在摩天轮转动一圈的过程中,游客可以观看到游乐场全景的时间是多少?
本小题分
一个半径为米的水轮如图所示,其圆心距离水面米,已知水轮按逆时针匀速转动,每秒转一圈,如果当水轮上点从水中浮现时图中点开始计算时间.
以过点且与水面垂直的直线为轴,过点且平行于水轮所在平面与水面的交线的直线为轴,建立如图所示的直角坐标系,试将点距离水面的高度单位:米表示为时间单位:秒的函数;
在水轮转动的任意一圈内,有多长时间点距水面的高度超过米?
本小题分
筒车是我国古代发明的一种水利灌概工具,因其经济又环保,至今还在农业生产中得到使用,现有一个筒车按逆时针方向匀速转动.每分钟转动圈,如图,将该简车抽象为圆,筒车上的盛水桶抽象为圆上的点,已知圆的半径为,圆心距离水面,且当圆上点从水中浮现时图中点开始计算时间.
根据如图所示的直角坐标系,将点到水面的距离单位:,在水面下,为负数表示为时间单位:的函数,并求时,点到水面的距离;
在点从开始转动的一圈内,点到水面的距离不低于的时间有多长?
本小题分
如图所示,一个摩天轮的半径为,轮子的底部在地面上处,如果此摩天轮按逆时针转动,每转一圈,且当摩天轮上某人经过点处点与摩天轮中心高度相同时开始计时.
求此人相对于地面的高度关于时间的关系式;
在摩天轮转动的一圈内,约有多长时间此人相对于地面的高度不小于
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查了在实际问题中建立三角函数模型的问题.考查了运用三角函数的最值,周期等问题,以及确定函数的解析式.
求出函数的解析式,再分析选项,即可得出结论.
【解答】
解:由题意,,,,
点,即,代入可得,
,,故A正确;
,
当时,,
点到轴的距离的最大值为,故B正确;
当时,,函数先增再减,故C错误;
当时,,的纵坐标为,,故D正确,
故选:.
2.【答案】
【解析】
【分析】
本题考查了三角函数模型应用问题,也考查了运算求解能力,是中档题.
建立适当的直角坐标系,用坐标表示点,建立高度与的函数关系式,从而求出对应的函数值.
【解答】
解:如图,设座舱距离地面最近的位置为点,以轴心为原点,与地面平行的直线为轴,建立直角坐标系.
设时,游客甲位于点,以为终边的角为,
根据摩天轮转一周大约需要,
可知座舱转动的角速度约为,
由题意可得,.
故选B.
3.【答案】
【解析】
【分析】
本题考查函数的图象与性质.
由实际问题确定解析式中的值以及函数的周期,从而求得,再由求得.
【解答】
解:设,
易知最大值为,最小值为,
所以又以及可得,,
当时,所以;
所以解析式为,
故选B.
4.【答案】
【解析】
【分析】
本题考查求三角函数模型的解析式,考查实际应用能力,属于中档题.
由题意,设,根据题意求出,,即可.
【解答】
解:由题意,设,
当时,,
,
故选B.
5.【答案】
【解析】
【分析】
本题主要考查求三角函数的解析式,三角函数的模型在实际生活中的应用,属于中档题.
由题得到最大值,求得的值,利用周期得到的值即可.
【解答】
解:由题目可知最大值为,
所以,得,
由于水轮自点开始分钟逆时针旋转圈,
所以,故.
6.【答案】
【解析】
【分析】
本题考查了三角函数模型的应用.
由到轴距离就是旋转角的正弦值的绝对值的两倍,再由初始位置是,从而确定三角函数关系式然后确定函数的图象.
【解答】
解:根据点的坐标可得,
故 .
设点,
则由三角函数的定义,可得,
即 ,
故,
因此点到轴的距离,
根据解析式可得选项图像符合条件.
故选C.
7.【答案】
【解析】
【分析】
本题考查函数的应用.
易知函数的最小正周期,可求出再利用初始位置的坐标求出,问题得以解决.
【解答】
解:由题意,设,
由题意知,函数的最小正周期,
,,
设函数解析式为秒针是顺时针走动.
又时,初始位置为,
时,.
,,
.
故选C.
8.【答案】
【解析】
【分析】
本题考查函数的图象与性质,建立直角坐标系,
由实际问题确定解析式中的值以及函数的周期,从而求得,再由求得,即可求出结果,属于基础题.
【解答】
解:如图所示,以点为坐标原点,以水平方向为轴,以所在直线为轴建立平面直角坐标系.
因为巨轮逆时针旋转且每分钟转一圈,则转动的角速度为每分钟,
经过分钟之后,转过的角度为,所以,在转动的过程中,点的纵坐标满足:
则吊舱距离地面的距离.
故选B.
9.【答案】
【解析】
【分析】
本题考查三角函数模型及函数的图象与性质,属于中档题.
由已知求出,得的解析式,然后利用正弦函数的性质逐一分析求解即可.
【解答】
解:在圆上,圆的半径,
又,,
所以,
由已知,即,,
又,所以,
所以A正确,
所以,
当时,,
由正弦函数的性质知,在上有增有减,
所以B错误
当时,,
则,
即点到轴的距离的最大值为,
所以C错误
当时,,
又在圆上,
所以,,
D正确.
故选AD.
10.【答案】
【解析】
【分析】
本题考查三角函数的模型应用,考查三角函数的解析式的求解于应用,考查了三角不等式的求解,属于中档题.
根据题意求出、、和,得到在时刻时点离地面的高度,进而可确定各选项正误.
【解答】
解:由图形知,可以以点为原点,所在直线为轴,与垂直的向右的方向为轴建立坐标系.
设摩天轮按逆时针方向旋转时,点离地面的高度为.
由题意,可得,
故点离地面的高度,
即在时刻时点离地面的高度,
化简得,
当时,,故A正确
若摩天轮转速减半,,则其周期变为原来的倍,故B错误
第,点距离地面的高度为;
第,点距离地面的高度为,
第和第时点距离地面的高度相同,故C正确
摩天轮转动一圈,点距离地面的高度不低于,
即,即,
,得,
或,
解得或,共,故D正确.
故选ACD.
11.【答案】
【解析】
【分析】
本题考查三角函数模型的应用,考查三角函数的性质问题,属于中档题.
由条件可求出,进而根据相关性质即可判断出各选项正误.
【解答】
解:由题意得,,
所以.
由容易求出,
又,所以,故选项A正确;
此时.
当时,
所以
于是,因此,故选项D错误;
由于
因而在上不单调递增,故选项B错误;
当时,,
所以,即,
所以,故选项C正确.
故选AC.
12.【答案】
【解析】
【分析】
本题考查了三角函数的图象与性质、三角函数求值,考查了推理能力与计算能力,属于中档题.
设点距离水面的高度米与秒的函数解析式为依题意可知的最大值为,最小为,可得,,解得,,解得当时,,得求出,可得所求的函数关系式为进而对各个选项依次判断即可.
【解答】
解:设点距离水面的高度米与秒的函数解析式为
依题意可知的最大值为,最小为,
,,解得,.
,解得.
,
当时,,得,,,
故所求的函数关系式为 , D错误,
令 ,
可得:,
,解得.
点第一次到达最高点要时间.A正确,
,B正确;
,C正确.
故选ABC.
13.【答案】
【解析】
【分析】
本题考查三角函数在实际问题中的应用,利用三角函数的特征,可设 , ,利用函数的周期以及求出与时间的关系即可.
【解答】
解:首先考虑建立直角坐标系,以最低点的切线作为轴,最低点作为坐标原点,建立如图所示的平面直角坐标系.
那么,风车上翼片端点所在位置可由函数,来刻画,而且 ,所以只需要考虑的解析式.
又设的初始位置在最低点,即.
在中, ,所以 .
而,,
所以,
则.
故答案为.
14.【答案】
【解析】
【分析】
本题考查了三角形面积公式的应用、二倍角公式和三角函数的最值,属于中档题.
可先求出个三角形的面积,再求出正方形的边长进而得到面积,最后得到答案.
【解答】
解:设等腰三角形的底角为,
由三角形的面积公式可得个等腰三角形的面积和为:
,
可得正方形边长为,
故正方形面积为,
所以所求占地面积为:
,
所以当,即时,占地面积最大,此时底角为.
故答案为.
15.【答案】
【解析】
【分析】
本题考查三角函数模型的实际应用,属于中档题
设,该公司日均盈利为万元,利用辅助角公式结合正弦型函数的性质可求得取最大值时满足的条件,结合诱导公式可求得的长.
【解答】
解:设,则,,
设该公司日均盈利为万元,
则,其中,
所以,其中为锐角,且,
由,解得,
因为,则,
故当时,取最大值,
此时.
故答案为.
16.【答案】
【解析】
【分析】
本题考查了函数的图象与应用问题,理解函数解析式中参数的物理意义,是解题的关键,属于中档题.
根据的最大值和最小值列方程组可求和,根据周期为秒可求,根据时,即可计算
【解答】
解:由题意,,
由图可知的最大值为,最小值为,即,解得,,
每秒转圈,周期,,
,
依题意,可知当时,,即,可得,
,
17.【答案】解:
设,
则,,
所以,
第一次到最高点旋转了半周期,
所以,
游客从最低点登上,所以,
故,
或.
令,
则
或,
所以
,
,,
所以,
因此,在乘坐一圈摩天轮的过程中,
该游客大约有最佳观景时间.
【解析】本题主要考查了三角函数的实际应用,属于中档题.
设,根据已知条件求出、、的值,可得出函数的解析式
解不等式,即可得解.
18.【答案】解:建立如图所示的直角坐标系,设角是以为始边,为终边的角,
每秒钟所转过的角为,则在时间内所转过的角为,
由题意可知水轮逆时针转动,得,
当时,,得,即,
故所求的函数关系式为.
由点露出水面,即.
即,
可得
解得:,
,,
.
在水轮转动的一圈内,有的时间点露出水面.
【解析】本题考查在实际问题中建立三角函数模型,考查三角函数的最值,周期,解析式,为中档题.
先建立直角坐标系,则,根据的最大和最小值求得和,利用周期求得,当时,,进而求得的值,则函数的表达式可得;
由于最大值为,即可求得的范围,得到所求.
19.【答案】解:由题意可知:设在时刻时点距离地面的高度.
,,,,
即.
又时,,,解得,
.
由知,,
,化为:.
,解得.
在距离地面超过的高度,游客可以观看到游乐场全景,那么在摩天轮转动一圈的过程中,游客可以观看到游乐场全景的时间是:.
【解析】本题考查了三角函数的解析式及其图象与性质、方程的解法,考查了推理能力与计算能力,属于中档题.
由题意可知:设在时刻时点距离地面的高度,,,,可得再根据时,解得,即可得出关于的函数解析式;
,解出即可得出.
20.【答案】解:如图,设水轮与轴正半轴交点为,轴与水面交点为.
根据题意,设 ,
,,
,,
因为函数的最小正周期,所以,
点距离水面的高度单位:米表示为时间单位:秒的函数是
根据题意,, ,
不妨设,则,
所以,
解得,, ,
所以,在水轮转动的任意一圈内,点距水面的高度超过米的时间有秒
【解析】本题考查三角函数模型应用问题,考查运算求解能力,属于中档题.
设水轮与轴正半轴交点为,轴与水面交点为,建立三角函数关系式表示高度关于时间的函数;
由关于的函数,令,求出时的取值范围,再计算有多长时间即可.
21.【答案】解:设,则点到水面的距离;
由题可知,与的夹角为;
在时间转过的角度为;
由图可知,点的纵坐标;
因此,则点到水面的距离;
当时,,所以点到水面的距离为;
根据题意,点到水面的距离不低于,应满足:
,得
因为筒车转动一圈需要秒,从开始转动一圈,则,
得
因此 ,解得
因此在点从开始转动的一圈内,点到水面的距离不低于的时间有.
【解析】本题考查三角函数的实际应用,属于一般题.
求出点的纵坐标,即可得点到水面的距离与时间的函数,令即可求此时点到水面的距离;
解即可判断.
22.【答案】解:设在时,摩天轮上某人在高处.
这时此人所转过的角为,
故在时,此人相对于地面的高度为.
由,
得,则,.
故在摩天轮转动的一圈内,此人有相对于地面的高度不小于.
【解析】本题考查三角函数模型,属于中档题.
根据已知条件,运用待定系数求出;
由,解得的范围,即可得到答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.8三角函数的简单应用北师大版( 2019)高中数学必修第二册
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时秒.经过秒后,水斗旋转到点,设的坐标为,其纵坐标满足则下列叙述错误的是( )
A.
B. 当时,点到轴的距离的最大值为
C. 当时,函数单调递减
D. 当时,
如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为,转盘直径为,设置有个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要游客甲坐上摩天轮的座舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
一观览车的主架示意图如图所示,其中为轮轴的中心,距地面即长,巨轮的半径为,,巨轮逆时针旋转且每分钟转动一圈若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为,则( )
A. B.
C. D.
如图,重庆欢乐谷的摩天轮被称为“重庆之眼”,其旋转半径为米,最高点距离地面米,开启后按逆时针方向旋转,旋转一周大约分钟.将摩天轮看成圆面,在该平面内,以过摩天轮的圆心且垂直于地平面的直线为轴,该直线与地平面的交点为坐标原点建立平面直角坐标系,某人在最低点的位置坐上摩天轮的座舱,摩天轮开始启动,并记该时刻为,则此人距离地面的高度与摩天轮运行时间单位:分钟的函数关系式为( )
A. B.
C. D.
一个半径为米的水轮示意图,水轮的圆心距离水面米,已知水轮自点开始分钟逆时针旋转圈,水轮上的点到水面的距离单位:米与时间单位:秒满足函数关系式,,,则有( )
A. , B. ,
C. , D. ,
如图所示,质点在半径为的圆周上按逆时针方向运动,其初始位置为,角速度为,那么点到轴的距离关于时间的函数图像大致为 ( )
A.
B.
C.
D.
为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系.设秒针针尖的位置为,若初始位置为,当秒针针尖从注:此时正常开始走时,点的纵坐标与时间的函数关系式为.( )
A.
B.
C.
D.
一观览车的主架示意图如图所示,其中为轮轴的中心,距地面即长,巨轮的半径长为,,巨轮逆时针旋转且每分钟转一圈,若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为( )
A. B.
C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如下图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足则下列叙述正确的是( )
A.
B. 当时,函数单调递增
C. 当时,点到轴的距离的最大值为
D. 当时,
如图,摩天轮的半径为,其中心点距离地面的高度为,摩天轮按逆时针方向做匀速转动,且转一圈,若摩天轮上点的起始位置在最高点处,则摩天轮转动过程中( )
A. 经过点距离地面
B. 若摩天轮转速减半,则其周期变为原来的倍
C. 第和第时点距离地面的高度相同
D. 摩天轮转动一圈,点距离地面的高度不低于的时间为
水车在古代是进行灌溉引水的工具,亦称“水转简车”,是一种以水流作动力,取水灌田的工具.据史料记载,水车发明于隋而盛于唐,距今已有多年的历史,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足 ,则下列叙述正确的是
A.
B. 当时,函数单调递增
C. 当时,
D. 当时,的最大值为
一半径为米的水轮如图所示,水轮圆心距离水面米,已知水轮每秒逆时针转动一圈,如果当水轮上点从水中浮现时图中点开始计时,则( )
A. 点第一次到达最高点需要秒
B. 当水轮转动秒时,点距离水面米
C. 当水轮转动秒时,点在水面下方,距离水面米
D. 点距离水面的高度米与秒的函数解析式为
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
如图所示,一个大风车的半径为,每旋转一周,最低点离地面若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点离地面的距离与时间之间的函数关系是 .
年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是一个正方形和四个以正方形的边为底边、腰长为的等腰三角形组成的图形如图所示,为使占地面积最大,则等腰三角形的底角为 .
如下图所示,某公司计划建造一座滨海公园,直线与均为海岸沿线,是以为直角的直角三角形,线段为“滨海栈桥”,线段将建成“阳光沙滩沿线”,线段将建成“灯塔沿线”现要求“滨海栈桥”长度维持在不变的基础上,可适当调整“阳光沙滩沿线”与“灯塔沿线”的设计长度预计建成后,每“阳光沙滩沿线”可让公司日均盈利万元,每“灯塔沿线”可让公司日均盈利万元,为使公司日均盈利最大,则应将“灯塔沿线”设计为 .
如图所示,一个半径为米的筒车绕其轴心按逆时针方向匀速转动,每旋转周恰需要秒,轴心距水面的高度为米.设筒车上的某个盛水筒到水面的距离为单位:米,在水面下时为负数将盛水筒上浮到水面的一点设为起始位置,则与时间单位:秒之间的关系为,确定、、、的值,则 .
四、解答题(本大题共6小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
本小题分
游乐场中的摩天轮沿逆时针方向匀速旋转,其中心距离地面,半径示意图如下,游客从最低点处登上摩天轮,其与地面的距离随着时间而变化,已知游客将在登上摩天轮后分钟到达最高点,自其登上摩天轮的时刻起,
求出其与地面的距离与时间的函数关系的解析式;
若距离地面高度超过时,为“最佳观景时间”,那么在乘坐一圈摩天轮的过程中,该游客大约有多少“最佳观景时间”?
本小题分
如图所示,一个水轮的半径为,水轮圆心距离水面,已知水轮每分钟转动圈,如果当水轮上的点从水中浮现图中点时开始计算时间.
求动点距水面的高度单位:米与时间单位:秒的函数关系与满足正弦函数模型
在水轮的一圈转动中,求点露出水面的时长?
本小题分
如图,摩天轮的半径为,圆心距地面的高度为已知摩天轮按逆时针方向匀速转动,每转动一圈.游客在摩天轮的舱位转到距离地面最近的位置进舱.
游客进入摩天轮的舱位,开始转动后,他距离地面的高度为,求关于的函数解析式;
已知在距离地面超过的高度,游客可以观看到游乐场全景,那么在摩天轮转动一圈的过程中,游客可以观看到游乐场全景的时间是多少?
本小题分
一个半径为米的水轮如图所示,其圆心距离水面米,已知水轮按逆时针匀速转动,每秒转一圈,如果当水轮上点从水中浮现时图中点开始计算时间.
以过点且与水面垂直的直线为轴,过点且平行于水轮所在平面与水面的交线的直线为轴,建立如图所示的直角坐标系,试将点距离水面的高度单位:米表示为时间单位:秒的函数;
在水轮转动的任意一圈内,有多长时间点距水面的高度超过米?
本小题分
筒车是我国古代发明的一种水利灌概工具,因其经济又环保,至今还在农业生产中得到使用,现有一个筒车按逆时针方向匀速转动.每分钟转动圈,如图,将该简车抽象为圆,筒车上的盛水桶抽象为圆上的点,已知圆的半径为,圆心距离水面,且当圆上点从水中浮现时图中点开始计算时间.
根据如图所示的直角坐标系,将点到水面的距离单位:,在水面下,为负数表示为时间单位:的函数,并求时,点到水面的距离;
在点从开始转动的一圈内,点到水面的距离不低于的时间有多长?
本小题分
如图所示,一个摩天轮的半径为,轮子的底部在地面上处,如果此摩天轮按逆时针转动,每转一圈,且当摩天轮上某人经过点处点与摩天轮中心高度相同时开始计时.
求此人相对于地面的高度关于时间的关系式;
在摩天轮转动的一圈内,约有多长时间此人相对于地面的高度不小于
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查了在实际问题中建立三角函数模型的问题.考查了运用三角函数的最值,周期等问题,以及确定函数的解析式.
求出函数的解析式,再分析选项,即可得出结论.
【解答】
解:由题意,,,,
点,即,代入可得,
,,故A正确;
,
当时,,
点到轴的距离的最大值为,故B正确;
当时,,函数先增再减,故C错误;
当时,,的纵坐标为,,故D正确,
故选:.
2.【答案】
【解析】
【分析】
本题考查了三角函数模型应用问题,也考查了运算求解能力,是中档题.
建立适当的直角坐标系,用坐标表示点,建立高度与的函数关系式,从而求出对应的函数值.
【解答】
解:如图,设座舱距离地面最近的位置为点,以轴心为原点,与地面平行的直线为轴,建立直角坐标系.
设时,游客甲位于点,以为终边的角为,
根据摩天轮转一周大约需要,
可知座舱转动的角速度约为,
由题意可得,.
故选B.
3.【答案】
【解析】
【分析】
本题考查函数的图象与性质.
由实际问题确定解析式中的值以及函数的周期,从而求得,再由求得.
【解答】
解:设,
易知最大值为,最小值为,
所以又以及可得,,
当时,所以;
所以解析式为,
故选B.
4.【答案】
【解析】
【分析】
本题考查求三角函数模型的解析式,考查实际应用能力,属于中档题.
由题意,设,根据题意求出,,即可.
【解答】
解:由题意,设,
当时,,
,
故选B.
5.【答案】
【解析】
【分析】
本题主要考查求三角函数的解析式,三角函数的模型在实际生活中的应用,属于中档题.
由题得到最大值,求得的值,利用周期得到的值即可.
【解答】
解:由题目可知最大值为,
所以,得,
由于水轮自点开始分钟逆时针旋转圈,
所以,故.
6.【答案】
【解析】
【分析】
本题考查了三角函数模型的应用.
由到轴距离就是旋转角的正弦值的绝对值的两倍,再由初始位置是,从而确定三角函数关系式然后确定函数的图象.
【解答】
解:根据点的坐标可得,
故 .
设点,
则由三角函数的定义,可得,
即 ,
故,
因此点到轴的距离,
根据解析式可得选项图像符合条件.
故选C.
7.【答案】
【解析】
【分析】
本题考查函数的应用.
易知函数的最小正周期,可求出再利用初始位置的坐标求出,问题得以解决.
【解答】
解:由题意,设,
由题意知,函数的最小正周期,
,,
设函数解析式为秒针是顺时针走动.
又时,初始位置为,
时,.
,,
.
故选C.
8.【答案】
【解析】
【分析】
本题考查函数的图象与性质,建立直角坐标系,
由实际问题确定解析式中的值以及函数的周期,从而求得,再由求得,即可求出结果,属于基础题.
【解答】
解:如图所示,以点为坐标原点,以水平方向为轴,以所在直线为轴建立平面直角坐标系.
因为巨轮逆时针旋转且每分钟转一圈,则转动的角速度为每分钟,
经过分钟之后,转过的角度为,所以,在转动的过程中,点的纵坐标满足:
则吊舱距离地面的距离.
故选B.
9.【答案】
【解析】
【分析】
本题考查三角函数模型及函数的图象与性质,属于中档题.
由已知求出,得的解析式,然后利用正弦函数的性质逐一分析求解即可.
【解答】
解:在圆上,圆的半径,
又,,
所以,
由已知,即,,
又,所以,
所以A正确,
所以,
当时,,
由正弦函数的性质知,在上有增有减,
所以B错误
当时,,
则,
即点到轴的距离的最大值为,
所以C错误
当时,,
又在圆上,
所以,,
D正确.
故选AD.
10.【答案】
【解析】
【分析】
本题考查三角函数的模型应用,考查三角函数的解析式的求解于应用,考查了三角不等式的求解,属于中档题.
根据题意求出、、和,得到在时刻时点离地面的高度,进而可确定各选项正误.
【解答】
解:由图形知,可以以点为原点,所在直线为轴,与垂直的向右的方向为轴建立坐标系.
设摩天轮按逆时针方向旋转时,点离地面的高度为.
由题意,可得,
故点离地面的高度,
即在时刻时点离地面的高度,
化简得,
当时,,故A正确
若摩天轮转速减半,,则其周期变为原来的倍,故B错误
第,点距离地面的高度为;
第,点距离地面的高度为,
第和第时点距离地面的高度相同,故C正确
摩天轮转动一圈,点距离地面的高度不低于,
即,即,
,得,
或,
解得或,共,故D正确.
故选ACD.
11.【答案】
【解析】
【分析】
本题考查三角函数模型的应用,考查三角函数的性质问题,属于中档题.
由条件可求出,进而根据相关性质即可判断出各选项正误.
【解答】
解:由题意得,,
所以.
由容易求出,
又,所以,故选项A正确;
此时.
当时,
所以
于是,因此,故选项D错误;
由于
因而在上不单调递增,故选项B错误;
当时,,
所以,即,
所以,故选项C正确.
故选AC.
12.【答案】
【解析】
【分析】
本题考查了三角函数的图象与性质、三角函数求值,考查了推理能力与计算能力,属于中档题.
设点距离水面的高度米与秒的函数解析式为依题意可知的最大值为,最小为,可得,,解得,,解得当时,,得求出,可得所求的函数关系式为进而对各个选项依次判断即可.
【解答】
解:设点距离水面的高度米与秒的函数解析式为
依题意可知的最大值为,最小为,
,,解得,.
,解得.
,
当时,,得,,,
故所求的函数关系式为 , D错误,
令 ,
可得:,
,解得.
点第一次到达最高点要时间.A正确,
,B正确;
,C正确.
故选ABC.
13.【答案】
【解析】
【分析】
本题考查三角函数在实际问题中的应用,利用三角函数的特征,可设 , ,利用函数的周期以及求出与时间的关系即可.
【解答】
解:首先考虑建立直角坐标系,以最低点的切线作为轴,最低点作为坐标原点,建立如图所示的平面直角坐标系.
那么,风车上翼片端点所在位置可由函数,来刻画,而且 ,所以只需要考虑的解析式.
又设的初始位置在最低点,即.
在中, ,所以 .
而,,
所以,
则.
故答案为.
14.【答案】
【解析】
【分析】
本题考查了三角形面积公式的应用、二倍角公式和三角函数的最值,属于中档题.
可先求出个三角形的面积,再求出正方形的边长进而得到面积,最后得到答案.
【解答】
解:设等腰三角形的底角为,
由三角形的面积公式可得个等腰三角形的面积和为:
,
可得正方形边长为,
故正方形面积为,
所以所求占地面积为:
,
所以当,即时,占地面积最大,此时底角为.
故答案为.
15.【答案】
【解析】
【分析】
本题考查三角函数模型的实际应用,属于中档题
设,该公司日均盈利为万元,利用辅助角公式结合正弦型函数的性质可求得取最大值时满足的条件,结合诱导公式可求得的长.
【解答】
解:设,则,,
设该公司日均盈利为万元,
则,其中,
所以,其中为锐角,且,
由,解得,
因为,则,
故当时,取最大值,
此时.
故答案为.
16.【答案】
【解析】
【分析】
本题考查了函数的图象与应用问题,理解函数解析式中参数的物理意义,是解题的关键,属于中档题.
根据的最大值和最小值列方程组可求和,根据周期为秒可求,根据时,即可计算
【解答】
解:由题意,,
由图可知的最大值为,最小值为,即,解得,,
每秒转圈,周期,,
,
依题意,可知当时,,即,可得,
,
17.【答案】解:
设,
则,,
所以,
第一次到最高点旋转了半周期,
所以,
游客从最低点登上,所以,
故,
或.
令,
则
或,
所以
,
,,
所以,
因此,在乘坐一圈摩天轮的过程中,
该游客大约有最佳观景时间.
【解析】本题主要考查了三角函数的实际应用,属于中档题.
设,根据已知条件求出、、的值,可得出函数的解析式
解不等式,即可得解.
18.【答案】解:建立如图所示的直角坐标系,设角是以为始边,为终边的角,
每秒钟所转过的角为,则在时间内所转过的角为,
由题意可知水轮逆时针转动,得,
当时,,得,即,
故所求的函数关系式为.
由点露出水面,即.
即,
可得
解得:,
,,
.
在水轮转动的一圈内,有的时间点露出水面.
【解析】本题考查在实际问题中建立三角函数模型,考查三角函数的最值,周期,解析式,为中档题.
先建立直角坐标系,则,根据的最大和最小值求得和,利用周期求得,当时,,进而求得的值,则函数的表达式可得;
由于最大值为,即可求得的范围,得到所求.
19.【答案】解:由题意可知:设在时刻时点距离地面的高度.
,,,,
即.
又时,,,解得,
.
由知,,
,化为:.
,解得.
在距离地面超过的高度,游客可以观看到游乐场全景,那么在摩天轮转动一圈的过程中,游客可以观看到游乐场全景的时间是:.
【解析】本题考查了三角函数的解析式及其图象与性质、方程的解法,考查了推理能力与计算能力,属于中档题.
由题意可知:设在时刻时点距离地面的高度,,,,可得再根据时,解得,即可得出关于的函数解析式;
,解出即可得出.
20.【答案】解:如图,设水轮与轴正半轴交点为,轴与水面交点为.
根据题意,设 ,
,,
,,
因为函数的最小正周期,所以,
点距离水面的高度单位:米表示为时间单位:秒的函数是
根据题意,, ,
不妨设,则,
所以,
解得,, ,
所以,在水轮转动的任意一圈内,点距水面的高度超过米的时间有秒
【解析】本题考查三角函数模型应用问题,考查运算求解能力,属于中档题.
设水轮与轴正半轴交点为,轴与水面交点为,建立三角函数关系式表示高度关于时间的函数;
由关于的函数,令,求出时的取值范围,再计算有多长时间即可.
21.【答案】解:设,则点到水面的距离;
由题可知,与的夹角为;
在时间转过的角度为;
由图可知,点的纵坐标;
因此,则点到水面的距离;
当时,,所以点到水面的距离为;
根据题意,点到水面的距离不低于,应满足:
,得
因为筒车转动一圈需要秒,从开始转动一圈,则,
得
因此 ,解得
因此在点从开始转动的一圈内,点到水面的距离不低于的时间有.
【解析】本题考查三角函数的实际应用,属于一般题.
求出点的纵坐标,即可得点到水面的距离与时间的函数,令即可求此时点到水面的距离;
解即可判断.
22.【答案】解:设在时,摩天轮上某人在高处.
这时此人所转过的角为,
故在时,此人相对于地面的高度为.
由,
得,则,.
故在摩天轮转动的一圈内,此人有相对于地面的高度不小于.
【解析】本题考查三角函数模型,属于中档题.
根据已知条件,运用待定系数求出;
由,解得的范围,即可得到答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
