11.2.1 三角形的内角 复习课件(19张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角 复习课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
知识构建Q例题引路
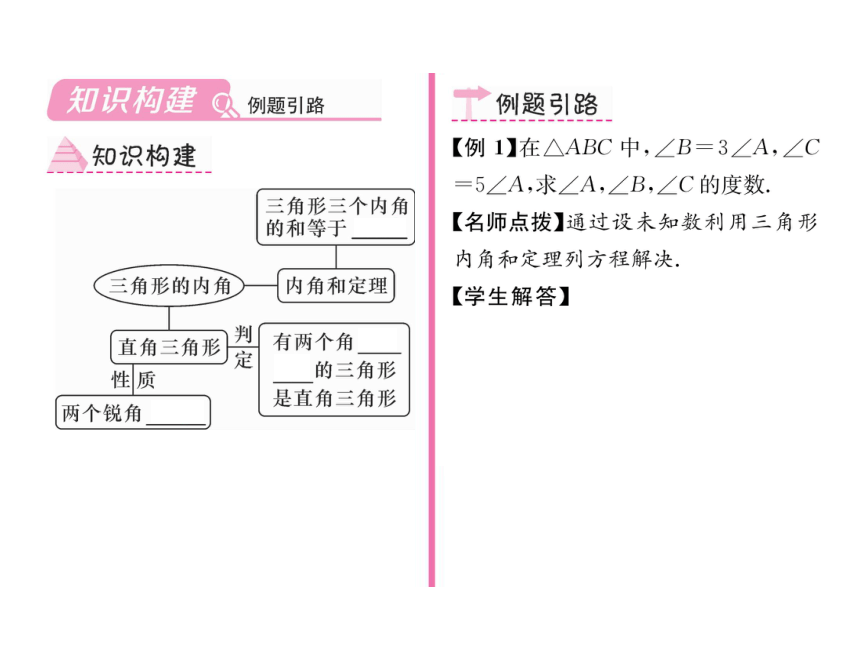
知识构建
三角形三个内角
的和等于180°
三角形的内角
内角和定理
直角三角形
判
有两个角互
性质
余的三角形
是直角三角形
两个锐角互余
广例题引路
【例1】在△ABC中,∠B=3∠A,∠C
=5/A,求/A,∠B,∠C的度数.
【名师点拨】通过设未知数利用三角形
内角和定理列方程解决.
【学生解答】解:设∠A=x°,则∠B=
3x°,∠C=5x°.
依题意,得x+3x+5x=180,
解得x=20,
.∠A=20°,∠B=60°,∠C=100°.
【例2】在△ABC巾,如果∠A-2∠B
-}∠C,那么△ABC是什么=角形?
【名师点拨】先根据三角形内角和定理
分别计算出三角形三个内角的度数,再
来判定
【学生解答】解:设∠A=x,
则∠B=2x,∠C=3x.
根据题意,得x十2x十3x=180°,
解得x=30°.
∴.∠A=30°,∠B=60°,∠C=90°,
∴.△ABC是直角三角形.
基础过关⊙逐点击破
知识点①三角形内角和定理
1.在△ABC中,若∠A=65°,∠B=45°,则∠C等于
(B)
A.110°
B.70°
C.65
D.45°
2.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数
为
(C)
A.120°
B.809
C.60°
D.40°
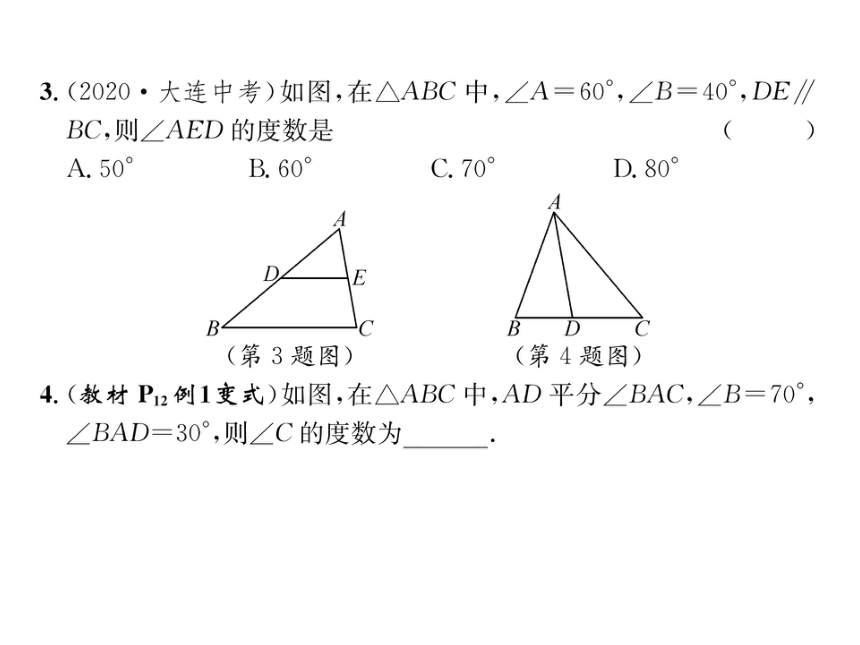
3.(2020·大连中考)如图,在△ABC中,∠A=60°,∠B=40°,DE∥
BC,则∠AED的度数是
(D)
A.50°
B.60°
C.70°
D.80°
B
B
D
(第3题图)
(第4题图)
4.(教材P2例1变式)如图,在△ABC中,AD平分∠BAC,∠B=70°,
∠BAD=30°,则∠C的度数为50
知识点②直角三角形的性质与判定
5.在一个直角三角形中,有一个锐角等于35°,则另一个锐角的度数
是
(C)
A.75°
B.65°
C.55°
D.45°
6.已知∠A=37°,∠B=53°,则△ABC为直角(选填“锐角”“直
角”或“钝角”)三角形
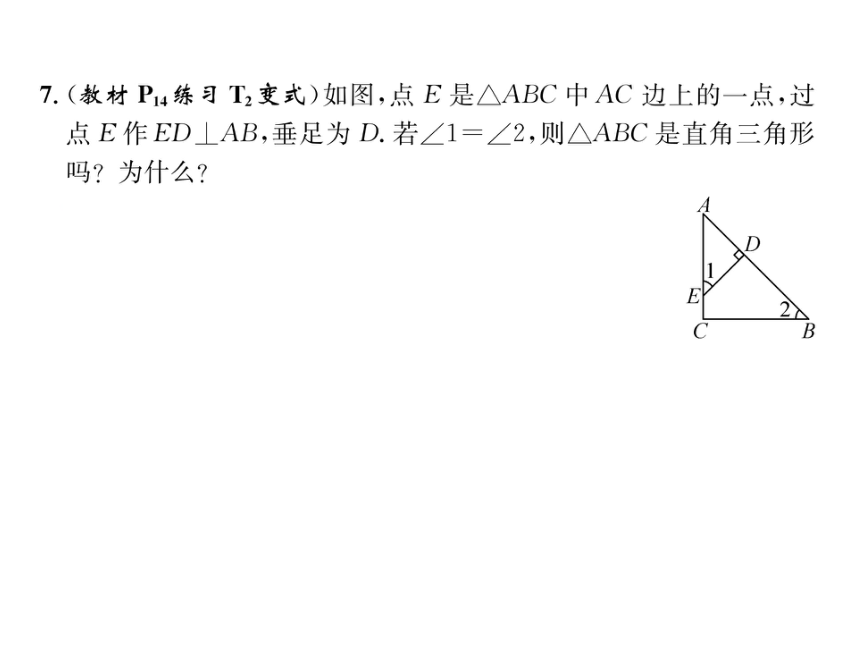
7.(教材P4练习T2变式)如图,点E是△ABC中AC边上的一点,过
点E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形
吗?为什么?
解:△ABC是直角三角形.理由如下:
.'ED AB.
∴∠ADE=90°,
∴.∠1+∠A=90°
又.∠1=∠2,
.∠2+∠A=90°,
.△ABC是直角三角形
易错点直角三角形中的直角顶点不确定导致漏解
8.如图,已知∠AOD=30°,点C是射线OD上的一个
动点.在点C的运动过程中,△AO℃恰好是直角三
角形,则此时∠A所有可能的度数为60或90°.
知识构建Q例题引路
知识构建
三角形三个内角
的和等于180°
三角形的内角
内角和定理
直角三角形
判
有两个角互
性质
余的三角形
是直角三角形
两个锐角互余
广例题引路
【例1】在△ABC中,∠B=3∠A,∠C
=5/A,求/A,∠B,∠C的度数.
【名师点拨】通过设未知数利用三角形
内角和定理列方程解决.
【学生解答】解:设∠A=x°,则∠B=
3x°,∠C=5x°.
依题意,得x+3x+5x=180,
解得x=20,
.∠A=20°,∠B=60°,∠C=100°.
【例2】在△ABC巾,如果∠A-2∠B
-}∠C,那么△ABC是什么=角形?
【名师点拨】先根据三角形内角和定理
分别计算出三角形三个内角的度数,再
来判定
【学生解答】解:设∠A=x,
则∠B=2x,∠C=3x.
根据题意,得x十2x十3x=180°,
解得x=30°.
∴.∠A=30°,∠B=60°,∠C=90°,
∴.△ABC是直角三角形.
基础过关⊙逐点击破
知识点①三角形内角和定理
1.在△ABC中,若∠A=65°,∠B=45°,则∠C等于
(B)
A.110°
B.70°
C.65
D.45°
2.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数
为
(C)
A.120°
B.809
C.60°
D.40°
3.(2020·大连中考)如图,在△ABC中,∠A=60°,∠B=40°,DE∥
BC,则∠AED的度数是
(D)
A.50°
B.60°
C.70°
D.80°
B
B
D
(第3题图)
(第4题图)
4.(教材P2例1变式)如图,在△ABC中,AD平分∠BAC,∠B=70°,
∠BAD=30°,则∠C的度数为50
知识点②直角三角形的性质与判定
5.在一个直角三角形中,有一个锐角等于35°,则另一个锐角的度数
是
(C)
A.75°
B.65°
C.55°
D.45°
6.已知∠A=37°,∠B=53°,则△ABC为直角(选填“锐角”“直
角”或“钝角”)三角形
7.(教材P4练习T2变式)如图,点E是△ABC中AC边上的一点,过
点E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形
吗?为什么?
解:△ABC是直角三角形.理由如下:
.'ED AB.
∴∠ADE=90°,
∴.∠1+∠A=90°
又.∠1=∠2,
.∠2+∠A=90°,
.△ABC是直角三角形
易错点直角三角形中的直角顶点不确定导致漏解
8.如图,已知∠AOD=30°,点C是射线OD上的一个
动点.在点C的运动过程中,△AO℃恰好是直角三
角形,则此时∠A所有可能的度数为60或90°.
