第12章 全等三角形 整合与提升练习课件(23张PPT)
文档属性
| 名称 | 第12章 全等三角形 整合与提升练习课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 00:00:00 | ||
图片预览


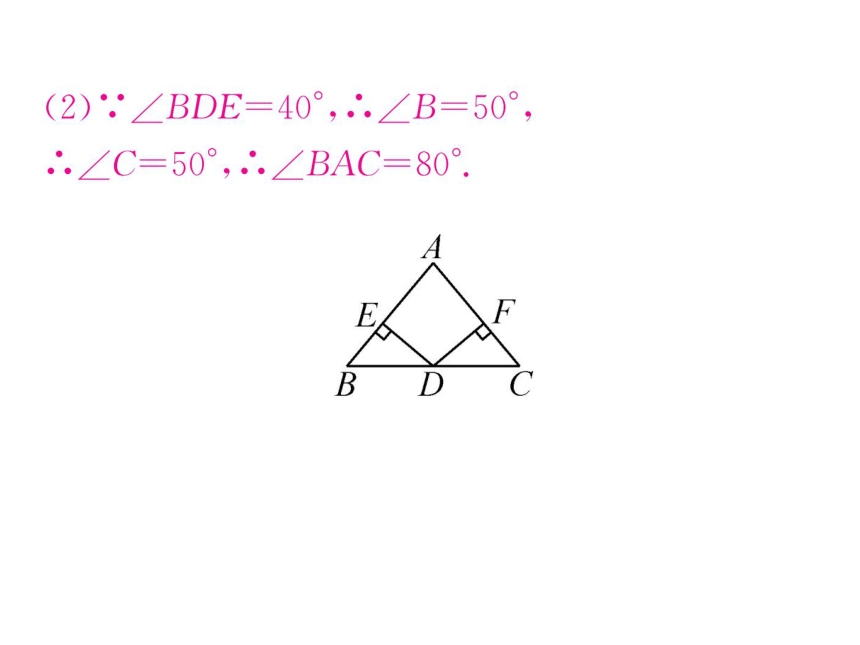

文档简介
(共23张PPT)
高频考点助力中考
考点①全等三角形的性质与判定
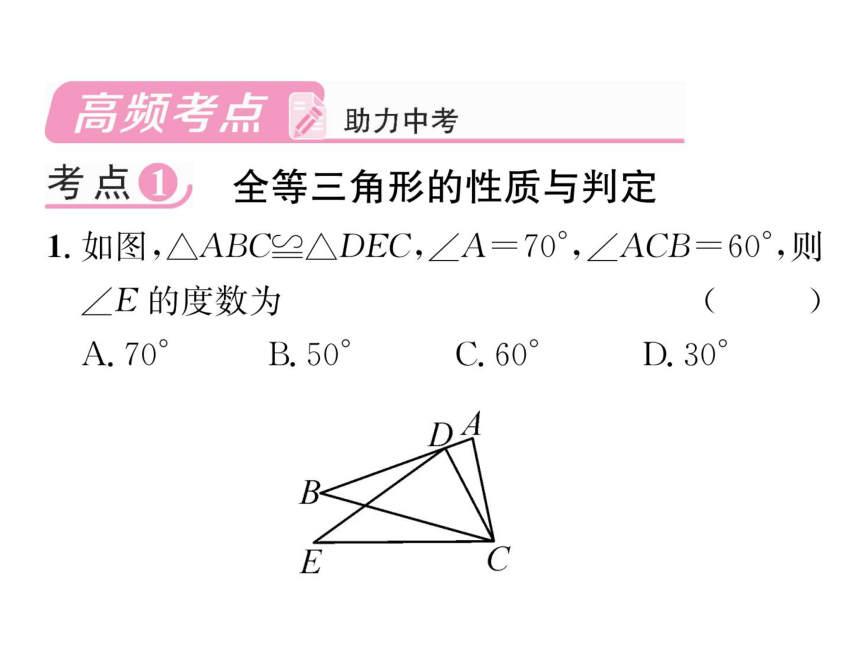
1.如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则
∠E的度数为
(B)
A.70°
B.50°
C.60°
D.30°
D
B
B
(第1题图)
(第2题图)
2.(2020·永州中考)如图,已知AB=DC,∠ABC
=∠DCB,能直接判断△ABC≌△DCB的方法
是
(A)
A.SAS
B.AAS
C.SSS
D.ASA
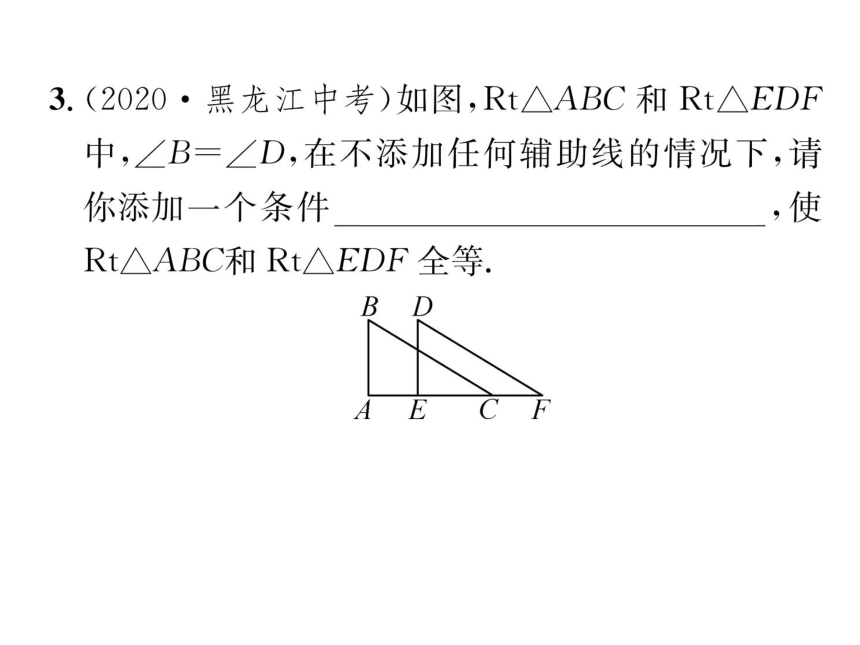
3.(2020·黑龙江中考)如图,Rt△ABC和Rt△EDF
中,∠B=∠D,在不添加任何辅助线的情况下,请
你添加一个条件AB=ED(答案不唯一),使
Rt△ABC和Rt△EDF全等
B
AE
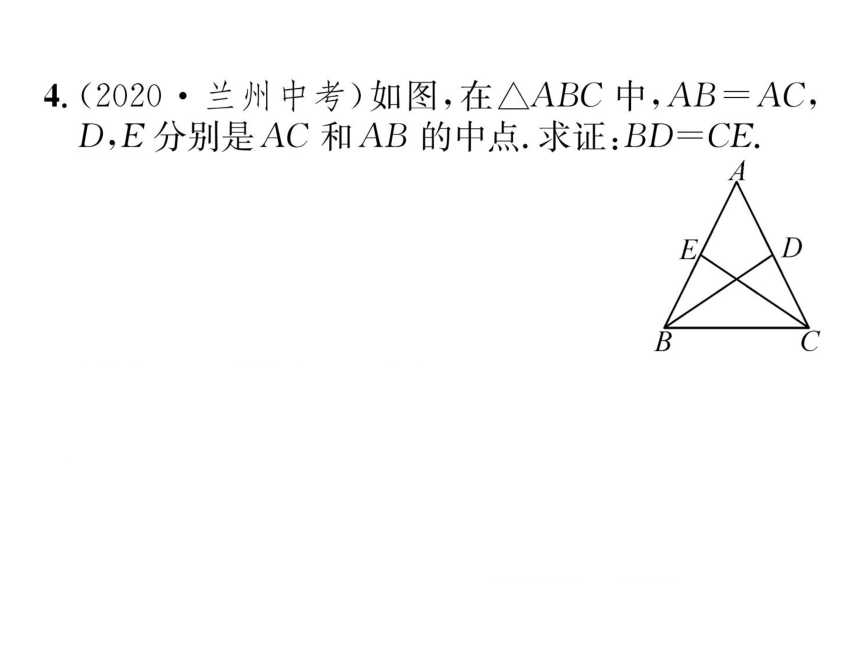
4.(2020·兰州中考)如图,在△ABC中,AB=AC,
D,E分别是AC和AB的中点.求证:BD=CE.
证明:AB=AC,
D,E分别为AC,AB的中点,
∴.AD=AE,
在△ABD和△ACE中,
(AB=AC,
∠A=∠A,
AD-AE,
'.△ABD≌△ACE(SAS),
∴.BD=CE
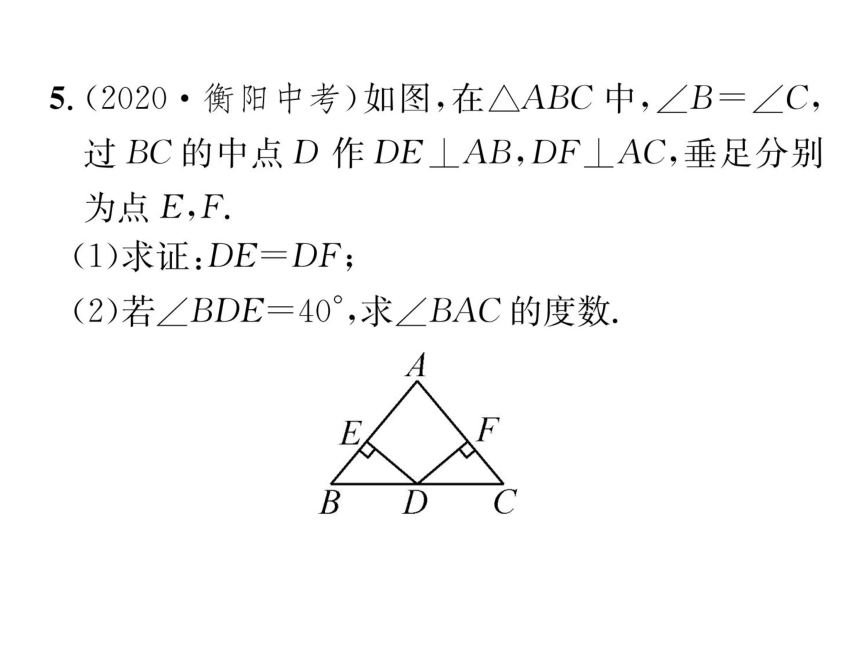
5.(2020·衡阳中考)如图,在△ABC中,∠B=∠C,
过BC的中点D作DE⊥AB,DF⊥AC,垂足分别
为点E,F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
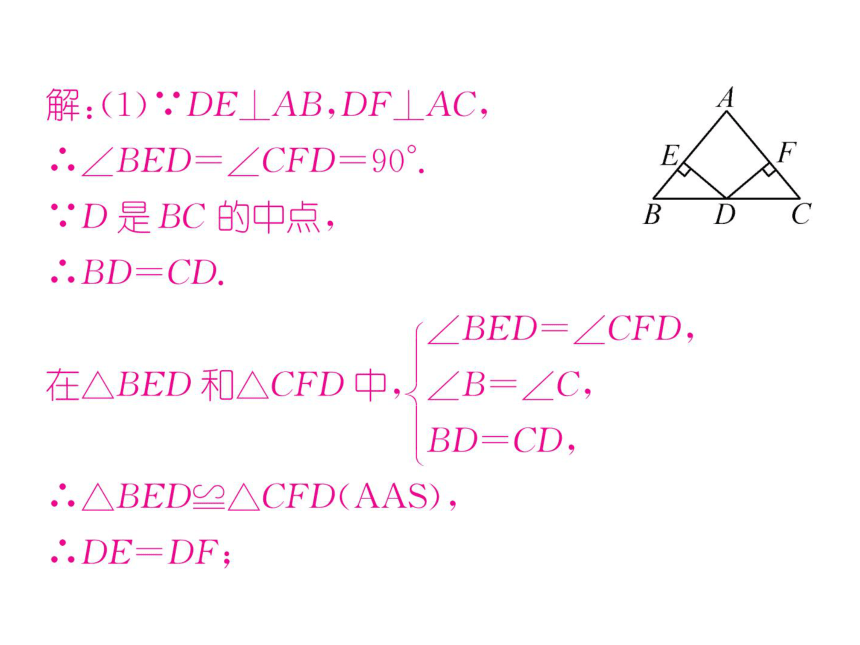
解:(1).DE⊥AB,DF⊥AC,
∴.∠BED=∠CFD=90°.
.D是BC的中点,
.'BD=CD.
'∠BED=∠CFD,
在△BED和△CFD中,∠B=∠C,
BD=CD,
.△BED≌△CFD(AAS),
.'.DE=DF;
(2).∠BDE=40°,∴.∠B=50°,
∴.∠C=50°,∴.∠BAC=80°.
考点②全等三角形的性质与判定的实际应用
6.如图,工人师傅要在墙壁的点O处用钻打孔,使孔
口从墙壁对面的点B处打出.墙壁厚35cm,点B
与点O的垂直距离AB长20cm,在点O处作一直
线平行于地面,再在直线上截取OC=35cm,过点
C作OC的垂线,在垂线上截取CD=20cm,连接
OD,然后沿着DO的方向打孔,结果钻头正好从点
B处打出,这是为什么?
解:在△AOB和△COD中,
OA=OC,
OAB-/OCD,
AB=CD,
口
.∴.△AOB≌△COD(SAS),
.∠AOB=∠COD
又.∠AOB+∠BC=180°,
..∠COD+∠BOC=180°,
即∠BOD=180°,
∴.D,O,B三点在同一条直线上.
故沿着DO的方向打孔,钻头正好从点B处打出.
高频考点助力中考
考点①全等三角形的性质与判定
1.如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则
∠E的度数为
(B)
A.70°
B.50°
C.60°
D.30°
D
B
B
(第1题图)
(第2题图)
2.(2020·永州中考)如图,已知AB=DC,∠ABC
=∠DCB,能直接判断△ABC≌△DCB的方法
是
(A)
A.SAS
B.AAS
C.SSS
D.ASA
3.(2020·黑龙江中考)如图,Rt△ABC和Rt△EDF
中,∠B=∠D,在不添加任何辅助线的情况下,请
你添加一个条件AB=ED(答案不唯一),使
Rt△ABC和Rt△EDF全等
B
AE
4.(2020·兰州中考)如图,在△ABC中,AB=AC,
D,E分别是AC和AB的中点.求证:BD=CE.
证明:AB=AC,
D,E分别为AC,AB的中点,
∴.AD=AE,
在△ABD和△ACE中,
(AB=AC,
∠A=∠A,
AD-AE,
'.△ABD≌△ACE(SAS),
∴.BD=CE
5.(2020·衡阳中考)如图,在△ABC中,∠B=∠C,
过BC的中点D作DE⊥AB,DF⊥AC,垂足分别
为点E,F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
解:(1).DE⊥AB,DF⊥AC,
∴.∠BED=∠CFD=90°.
.D是BC的中点,
.'BD=CD.
'∠BED=∠CFD,
在△BED和△CFD中,∠B=∠C,
BD=CD,
.△BED≌△CFD(AAS),
.'.DE=DF;
(2).∠BDE=40°,∴.∠B=50°,
∴.∠C=50°,∴.∠BAC=80°.
考点②全等三角形的性质与判定的实际应用
6.如图,工人师傅要在墙壁的点O处用钻打孔,使孔
口从墙壁对面的点B处打出.墙壁厚35cm,点B
与点O的垂直距离AB长20cm,在点O处作一直
线平行于地面,再在直线上截取OC=35cm,过点
C作OC的垂线,在垂线上截取CD=20cm,连接
OD,然后沿着DO的方向打孔,结果钻头正好从点
B处打出,这是为什么?
解:在△AOB和△COD中,
OA=OC,
OAB-/OCD,
AB=CD,
口
.∴.△AOB≌△COD(SAS),
.∠AOB=∠COD
又.∠AOB+∠BC=180°,
..∠COD+∠BOC=180°,
即∠BOD=180°,
∴.D,O,B三点在同一条直线上.
故沿着DO的方向打孔,钻头正好从点B处打出.
