12.1 全等三角形 复习课件(19张PPT)
文档属性
| 名称 | 12.1 全等三角形 复习课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 11:47:51 | ||
图片预览



文档简介
(共19张PPT)
第引章全等三角形
12.1
全等三角形
知识构建Q
例题引路
知识构建
能够完全重合的两个三角形
定义
全等用符
对应顶
号“≌”
点,对
有关
全等表示
应边,
概念三角形方法
表示,读
对应角
作“全等
性质
”
对应边
对应角
对应边上的中
相等
相等
线、高分别相
等,对应角的
平分线相等,
周长相等,
面积相等
例题引路
【例1】如图,沿直线BD对
折,△ABD和△CBD重
合,则△ABD≌
AB的对应边是
,BD的对应
边是
,∠ADB的对应角是
【学生解答】△CBD;CB;BD;∠CDB
【例2】如图,已知△ABD≌
△ACD,且点B,D,C在同一
条直线上,那么AD与BC有
怎样的位置关系?为什么?
【名师点拨】由△ABD≌△ACD可推出
∠ADB与∠ADC相等,而∠ADB与
∠ADC又互补,则可求得∠ADB的度
数,从而可得出AD与BC的位置关系.
【学生解答】解:ADBC.理由如下:
.△ABD≌△ACD,.∠ADB=
∠ADC.又.∠ADB+∠ADC=180°,
.∠ADB=∠ADC=90°,
∴.AD⊥BC.
基础过关逐点击破
知识点①全等形和全等三角形的有关概念
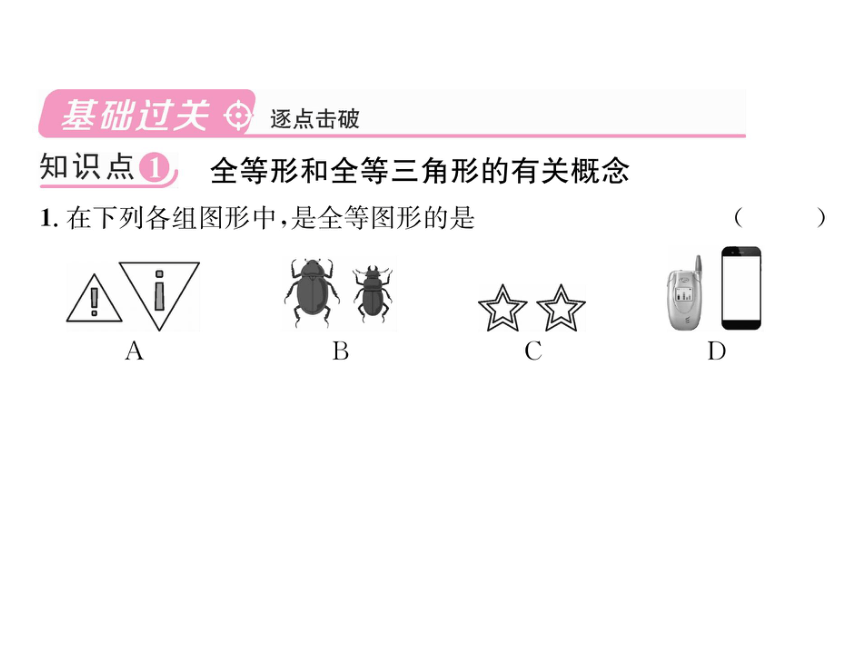
1.在下列各组图形中,是全等图形的是
意卷
☆☆
A
B
C
D
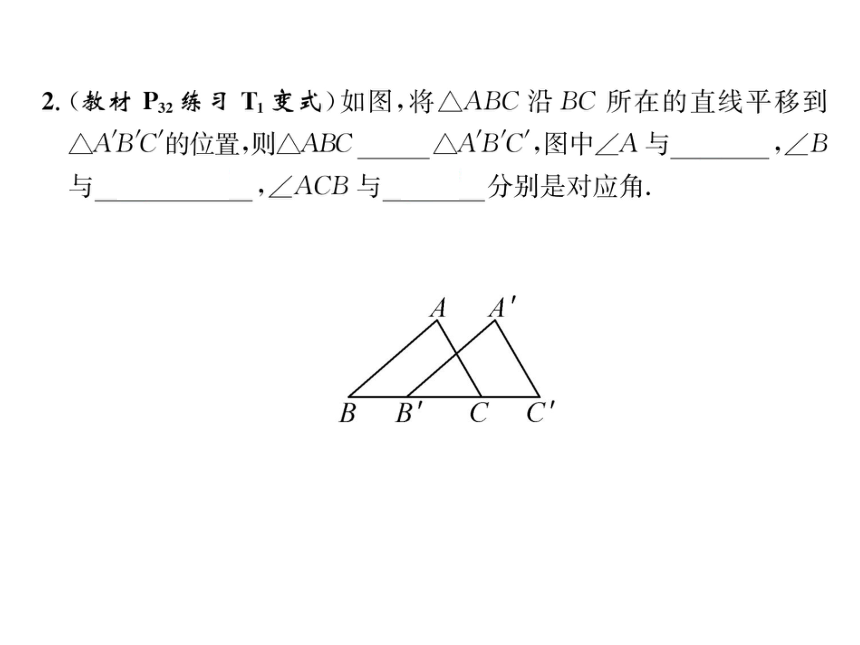
2.(教材P32练习T1变式)如图,将△ABC沿BC所在的直线平移到
△A'B'C的位置,则△ABC≌△A'B'C,图中∠A与∠A',∠B
与∠A'B'C',∠ACB与∠C分别是对应角.
y
B(0,2)
51°
A(1,0)x
B B'C
B'
(第2题图)
(第3题图)
(第4题图)
知识点②全等三角形的性质
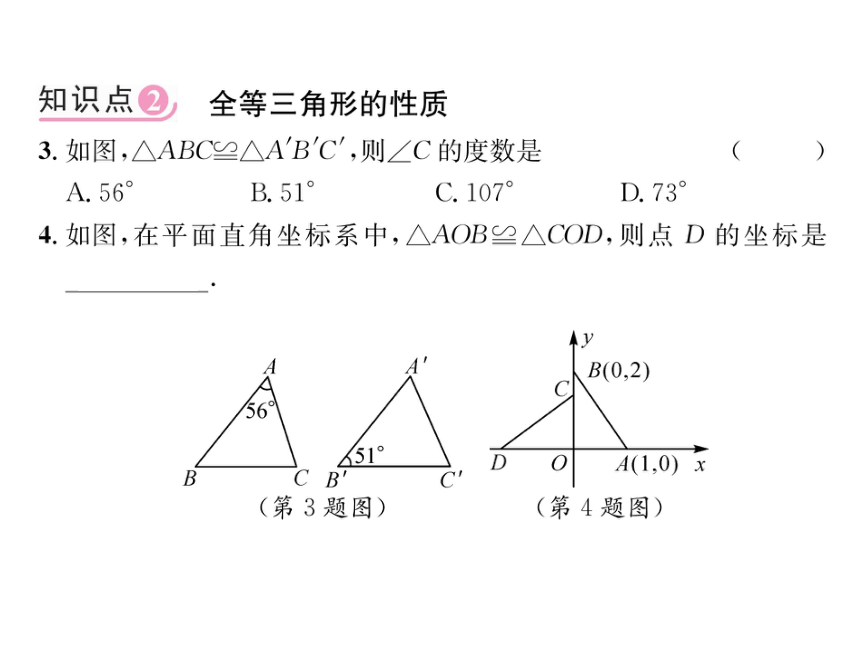
3.如图,△ABC≌△A'B'C',则∠C的度数是
(D
)
A.56°
B.51°
C.107°
D.73°
4.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是
(-2,0)。
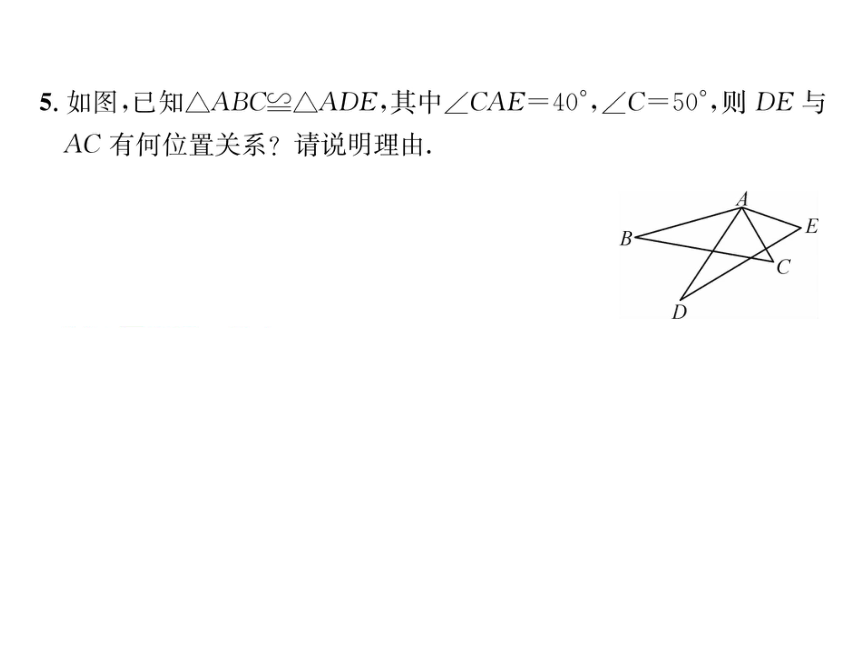
5.如图,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与
AC有何位置关系?请说明理由,
解:DE与AC互相垂直,
理由如下:设AC与DE相交于点F.
.△ABC≌△ADE,∴.∠C=∠E=50°.
又.∠CAE=40°,
.∴.∠AFE=180°-∠E-∠CAE=180°-50-40°=90°,
∴.DE AC
易错点不能准确确定全等三角形的对应关系
6.如图,△ABC2△CDA,并且BC=DA,那么下列结论错误的是(C
A.∠1=∠2
B.∠ACB=∠DAC
C.AB-AD
D.∠B=∠D
第引章全等三角形
12.1
全等三角形
知识构建Q
例题引路
知识构建
能够完全重合的两个三角形
定义
全等用符
对应顶
号“≌”
点,对
有关
全等表示
应边,
概念三角形方法
表示,读
对应角
作“全等
性质
”
对应边
对应角
对应边上的中
相等
相等
线、高分别相
等,对应角的
平分线相等,
周长相等,
面积相等
例题引路
【例1】如图,沿直线BD对
折,△ABD和△CBD重
合,则△ABD≌
AB的对应边是
,BD的对应
边是
,∠ADB的对应角是
【学生解答】△CBD;CB;BD;∠CDB
【例2】如图,已知△ABD≌
△ACD,且点B,D,C在同一
条直线上,那么AD与BC有
怎样的位置关系?为什么?
【名师点拨】由△ABD≌△ACD可推出
∠ADB与∠ADC相等,而∠ADB与
∠ADC又互补,则可求得∠ADB的度
数,从而可得出AD与BC的位置关系.
【学生解答】解:ADBC.理由如下:
.△ABD≌△ACD,.∠ADB=
∠ADC.又.∠ADB+∠ADC=180°,
.∠ADB=∠ADC=90°,
∴.AD⊥BC.
基础过关逐点击破
知识点①全等形和全等三角形的有关概念
1.在下列各组图形中,是全等图形的是
意卷
☆☆
A
B
C
D
2.(教材P32练习T1变式)如图,将△ABC沿BC所在的直线平移到
△A'B'C的位置,则△ABC≌△A'B'C,图中∠A与∠A',∠B
与∠A'B'C',∠ACB与∠C分别是对应角.
y
B(0,2)
51°
A(1,0)x
B B'C
B'
(第2题图)
(第3题图)
(第4题图)
知识点②全等三角形的性质
3.如图,△ABC≌△A'B'C',则∠C的度数是
(D
)
A.56°
B.51°
C.107°
D.73°
4.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是
(-2,0)。
5.如图,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与
AC有何位置关系?请说明理由,
解:DE与AC互相垂直,
理由如下:设AC与DE相交于点F.
.△ABC≌△ADE,∴.∠C=∠E=50°.
又.∠CAE=40°,
.∴.∠AFE=180°-∠E-∠CAE=180°-50-40°=90°,
∴.DE AC
易错点不能准确确定全等三角形的对应关系
6.如图,△ABC2△CDA,并且BC=DA,那么下列结论错误的是(C
A.∠1=∠2
B.∠ACB=∠DAC
C.AB-AD
D.∠B=∠D
