第十二章 证明三角形全等的基本思路 专项训练课件(19张PPT)
文档属性
| 名称 | 第十二章 证明三角形全等的基本思路 专项训练课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 15:00:37 | ||
图片预览

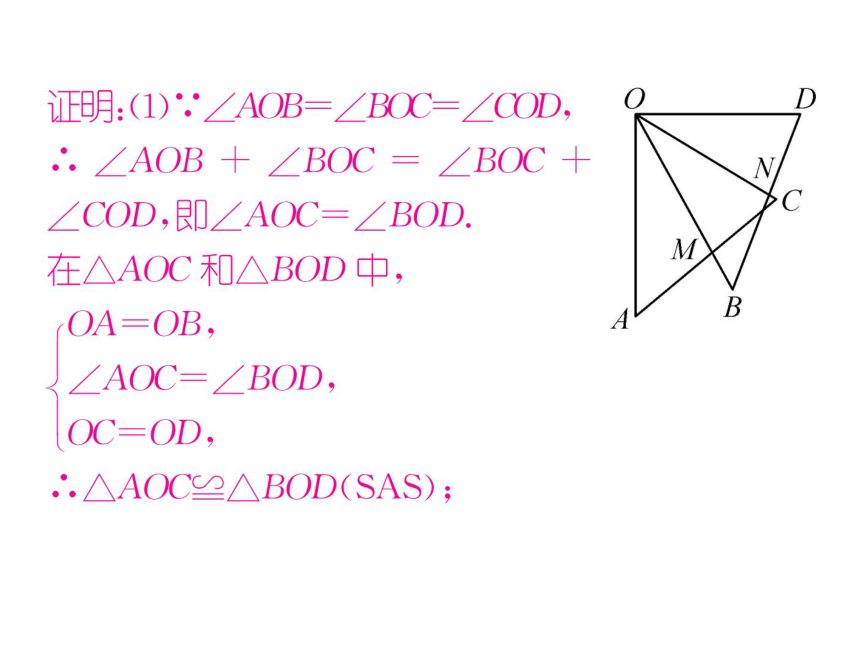
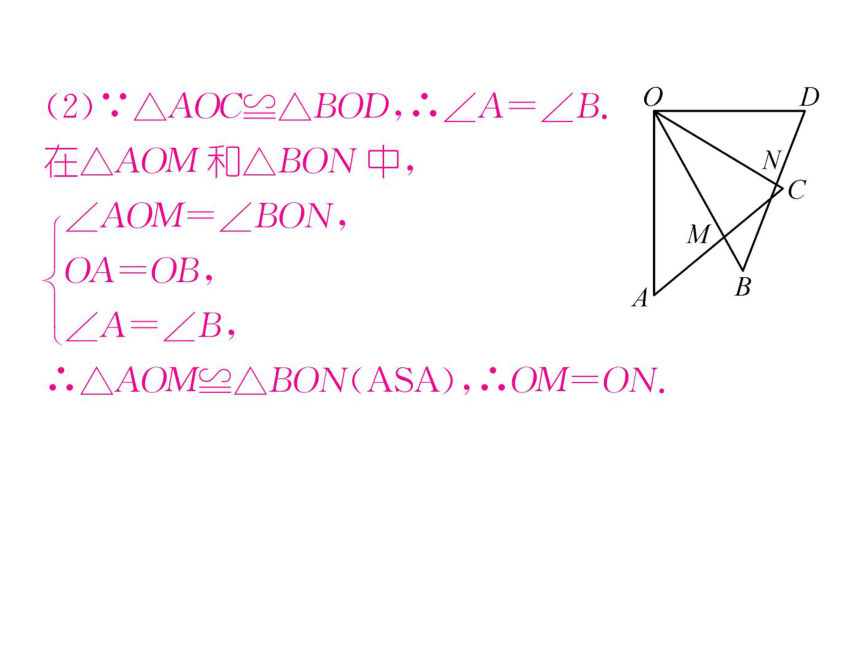
文档简介
(共19张PPT)
类型①已知两边对应相等
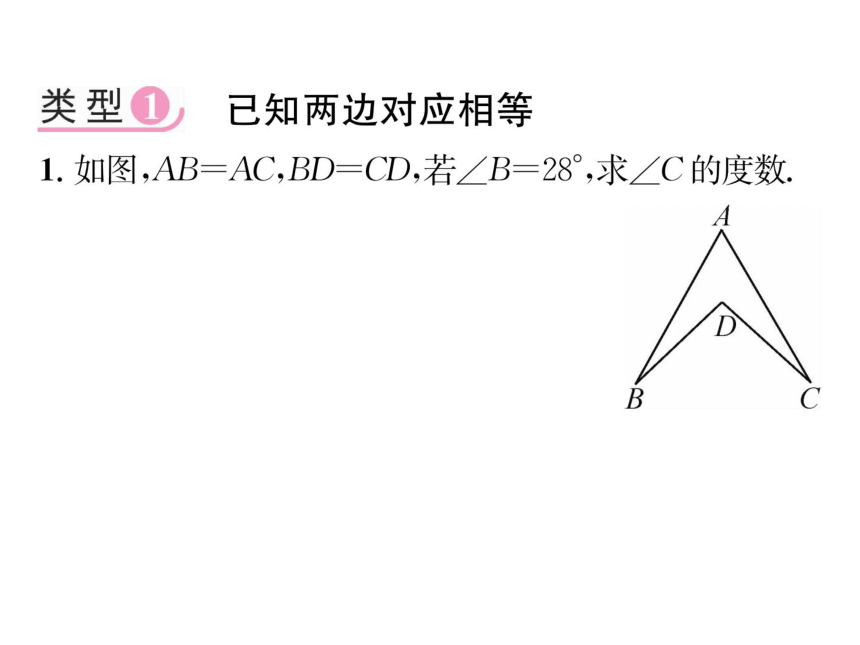
1.如图,AB=AC,BD=CD,若∠B=28°,求∠C的度数.
解:连接AD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴.△ABD≌△ACD(SSS),
.∠C=∠B=28.
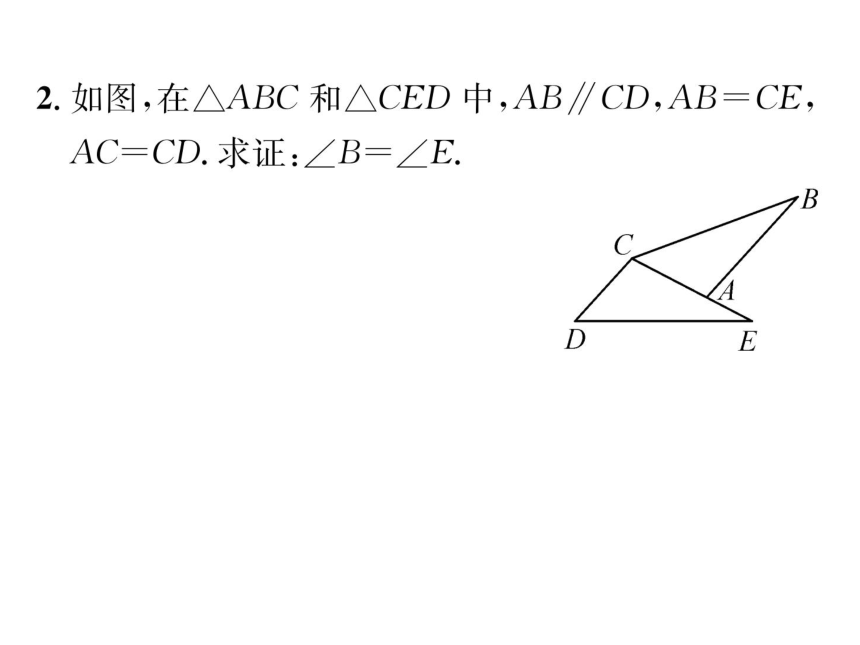
2.如图,在△ABC和△CED中,AB∥CD,AB=CE,
AC=CD.求证:∠B=∠E.
证明:.AB∥CD,
B
∴.∠DCE=∠CAB.
在△CAB和△DCE中,
(AB=CE,
∠CAB=∠DCE,
AC=CD,
∴.△CAB≌△DCE(SAS),
∴.∠B=∠E
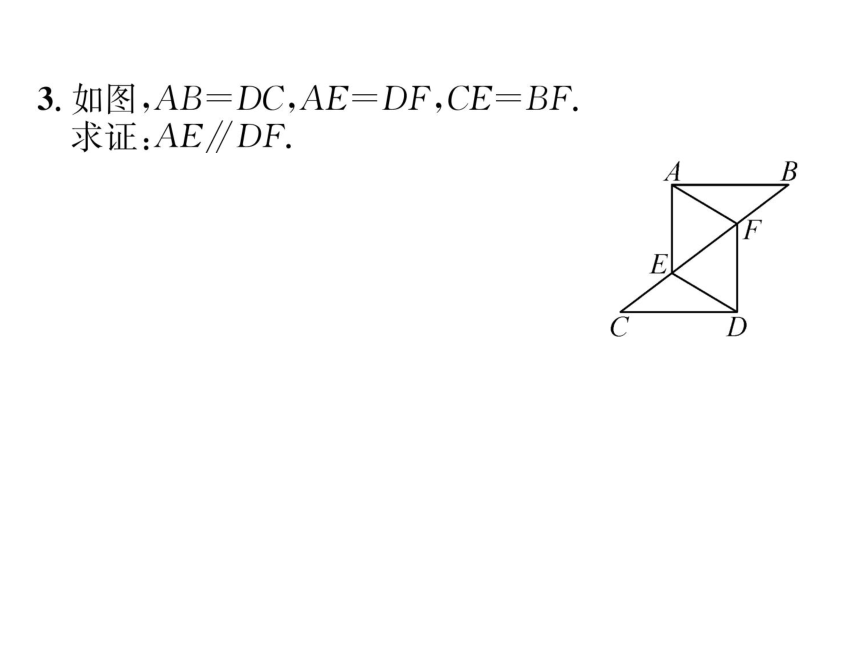
3.如图,AB=DC,AE=DF,CE=BF.
求证:AE∥DF.
证明:.CE=BF,
'.CE十EF=BF+EF,即CF=BE
在△CDF和△BAE中,
DF-AE,
DC=AB,
CF=BE,
∴.△CDF≌△BAE(SSS),
∴.∠CFD=∠BEA,
.AE∥DF.
A
D
B
C
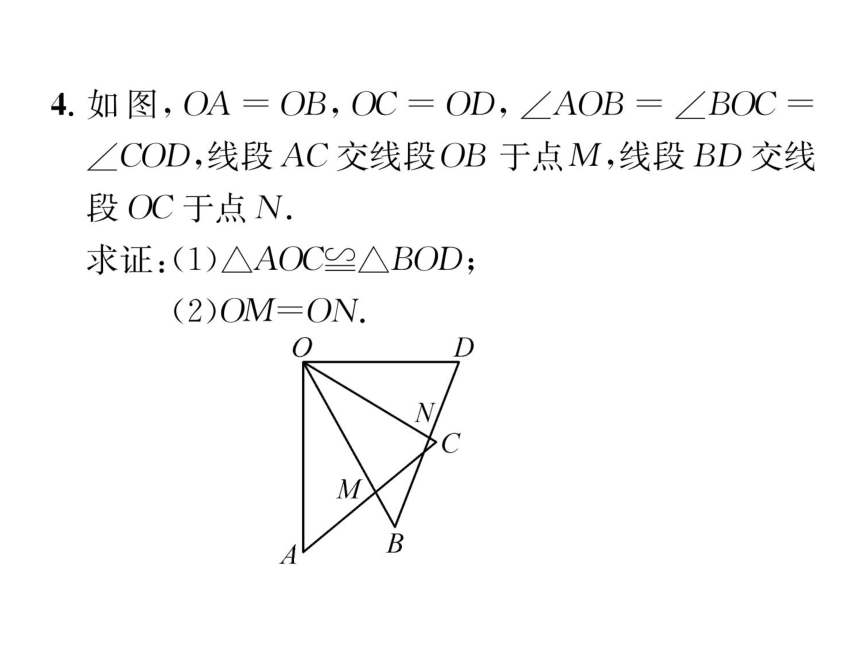
4.如图,OA=OB,OC=OD,∠AOB=∠BOC=
∠COD,线段AC交线段OB于点M,线段BD交线
段OC于点V.
求证:(1)△AOC2△BOD;
(2)OM-ON.
正明:(1).'∠AOB=∠BQC=∠COD,
∴.∠AOB+∠BOC=∠BOC+
∠COD,即∠AOC=∠BOD.
在△AOC和△BOD中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
∴.△AOC≌△BOD(SAS);
(2).△AOC≌△BOD,.∠A=∠B.
在△AOM和△BON中,
(∠AOM=∠BON,
OA=OB,
∠A=∠B,
.'.△AOM≌△BON(ASA),∴.OM=ON.
类型②已知一边及其邻角对应相等
5.如图,已知AB=AC,∠B=∠C
求证:△ABE≌△ACD.
证明:在△ABE和△ACD中,
í∠A=∠A,
AB=AC,
D
∠B=∠C,
∴.△ABE≌△ACD(ASA).
6.如图,已知点B,E,C,F在同一条直线上,AB=
DE,∠A=∠D,AC∥DF.求证:BE=CF.
证明:.AC∥DF,∴.∠ACB=∠F.
在△ABC和△DEF中,
(∠A=∠D,
∠ACB=∠F,
AB=DE,
'.△ABC≌△DEF(AAS),
.'BC=EF,
.'.BC-CE=EF-CE,
即BE=CF.
类型③已知一边及其对角对应相等
7.如图,CA=CD,∠B=∠E,∠BCE=∠ACD.
求证:AB=DE.
证明:∠BCE=∠ACD,
'.∠BCE+∠ECA=∠ECA+
∠ACD,即∠ACB=∠DCE.
在△ABC和△DEC中,
(∠ACB=∠DCE,
∠B=∠E,
CA=CD,
.△ABC≌△DEC(AAS),
∴.AB=DE.
类型④已知两角对应相等
8.如图,在四边形ABCD中,点E在AD上,∠BCE=
∠ACD=90°,∠BAC=∠D,BC=CE.
求证:AC=CD.
证明:.'∠BCE=∠ACD=90°,
'.∠ACB+∠ACE=∠ACE+∠DCE,
∴.∠ACB=∠DCE.
D
在△ABC和△DEC中,
(∠BAC=∠D,
∠ACB=∠DCE,
BC=EC,
.'.△ABC≌△DEC(AAS),
..AC=CD.
9.如图,已知AC平分∠BAD,∠1=∠2.
求证:AB=AD.
证明:.AC平分∠BAD,
∴.∠BAC=∠DAC.
D
.∠1=∠2,
.∴.180°-∠1=180°-∠2,
即∠ABC=∠ADC.
在△ABC和△ADC中,
(∠BAC=∠DAC,
∠ABC=∠ADC,
AC=AC,
∴.△ABC2△ADC(AAS),
.'.AB=AD.
类型①已知两边对应相等
1.如图,AB=AC,BD=CD,若∠B=28°,求∠C的度数.
解:连接AD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴.△ABD≌△ACD(SSS),
.∠C=∠B=28.
2.如图,在△ABC和△CED中,AB∥CD,AB=CE,
AC=CD.求证:∠B=∠E.
证明:.AB∥CD,
B
∴.∠DCE=∠CAB.
在△CAB和△DCE中,
(AB=CE,
∠CAB=∠DCE,
AC=CD,
∴.△CAB≌△DCE(SAS),
∴.∠B=∠E
3.如图,AB=DC,AE=DF,CE=BF.
求证:AE∥DF.
证明:.CE=BF,
'.CE十EF=BF+EF,即CF=BE
在△CDF和△BAE中,
DF-AE,
DC=AB,
CF=BE,
∴.△CDF≌△BAE(SSS),
∴.∠CFD=∠BEA,
.AE∥DF.
A
D
B
C
4.如图,OA=OB,OC=OD,∠AOB=∠BOC=
∠COD,线段AC交线段OB于点M,线段BD交线
段OC于点V.
求证:(1)△AOC2△BOD;
(2)OM-ON.
正明:(1).'∠AOB=∠BQC=∠COD,
∴.∠AOB+∠BOC=∠BOC+
∠COD,即∠AOC=∠BOD.
在△AOC和△BOD中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
∴.△AOC≌△BOD(SAS);
(2).△AOC≌△BOD,.∠A=∠B.
在△AOM和△BON中,
(∠AOM=∠BON,
OA=OB,
∠A=∠B,
.'.△AOM≌△BON(ASA),∴.OM=ON.
类型②已知一边及其邻角对应相等
5.如图,已知AB=AC,∠B=∠C
求证:△ABE≌△ACD.
证明:在△ABE和△ACD中,
í∠A=∠A,
AB=AC,
D
∠B=∠C,
∴.△ABE≌△ACD(ASA).
6.如图,已知点B,E,C,F在同一条直线上,AB=
DE,∠A=∠D,AC∥DF.求证:BE=CF.
证明:.AC∥DF,∴.∠ACB=∠F.
在△ABC和△DEF中,
(∠A=∠D,
∠ACB=∠F,
AB=DE,
'.△ABC≌△DEF(AAS),
.'BC=EF,
.'.BC-CE=EF-CE,
即BE=CF.
类型③已知一边及其对角对应相等
7.如图,CA=CD,∠B=∠E,∠BCE=∠ACD.
求证:AB=DE.
证明:∠BCE=∠ACD,
'.∠BCE+∠ECA=∠ECA+
∠ACD,即∠ACB=∠DCE.
在△ABC和△DEC中,
(∠ACB=∠DCE,
∠B=∠E,
CA=CD,
.△ABC≌△DEC(AAS),
∴.AB=DE.
类型④已知两角对应相等
8.如图,在四边形ABCD中,点E在AD上,∠BCE=
∠ACD=90°,∠BAC=∠D,BC=CE.
求证:AC=CD.
证明:.'∠BCE=∠ACD=90°,
'.∠ACB+∠ACE=∠ACE+∠DCE,
∴.∠ACB=∠DCE.
D
在△ABC和△DEC中,
(∠BAC=∠D,
∠ACB=∠DCE,
BC=EC,
.'.△ABC≌△DEC(AAS),
..AC=CD.
9.如图,已知AC平分∠BAD,∠1=∠2.
求证:AB=AD.
证明:.AC平分∠BAD,
∴.∠BAC=∠DAC.
D
.∠1=∠2,
.∴.180°-∠1=180°-∠2,
即∠ABC=∠ADC.
在△ABC和△ADC中,
(∠BAC=∠DAC,
∠ABC=∠ADC,
AC=AC,
∴.△ABC2△ADC(AAS),
.'.AB=AD.
