第十二章 全等三角形的性质与判定 专线训练课件(24张PPT)
文档属性
| 名称 | 第十二章 全等三角形的性质与判定 专线训练课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 15:02:39 | ||
图片预览

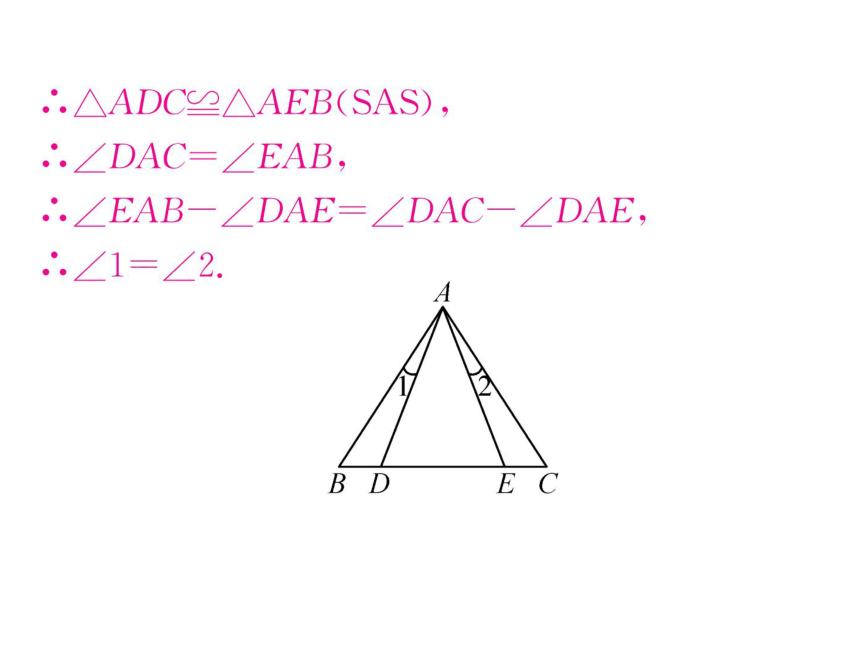


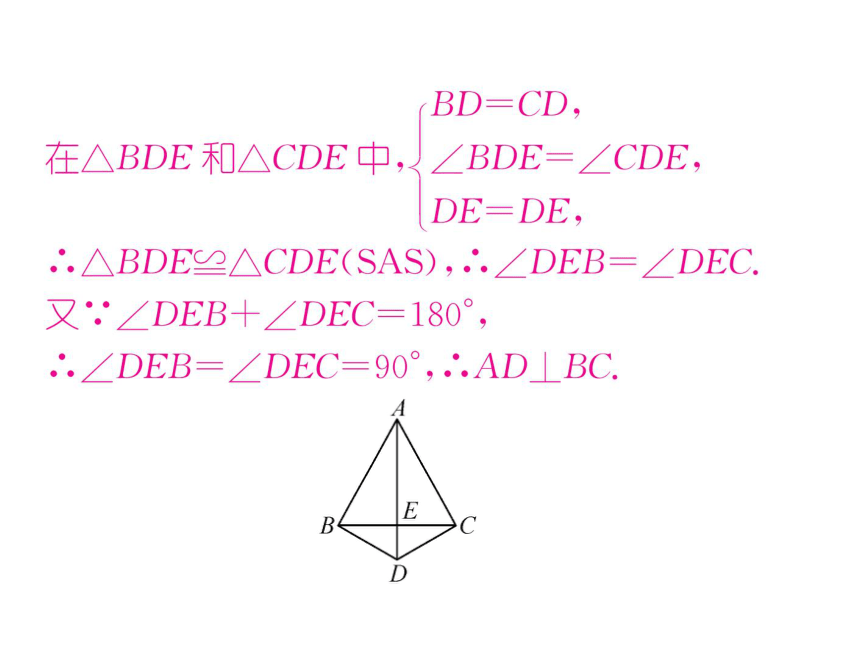


文档简介
(共24张PPT)
类型①基础类(证一次全等)
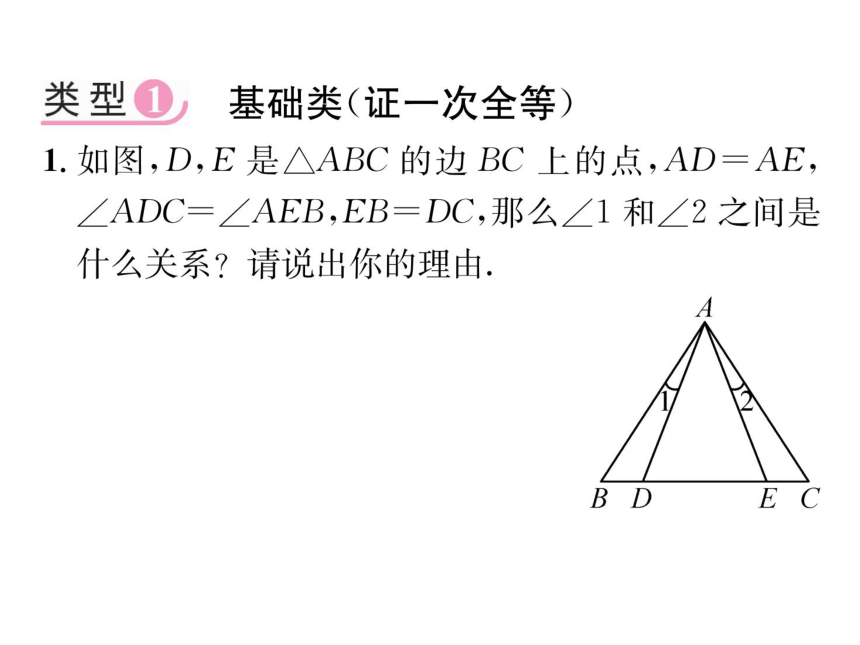
1.如图,D,E是△ABC的边BC上的点,AD=AE,
∠ADC=∠AEB,EB=DC,那么∠1和∠2之间是
什么关系?请说出你的理由,
解:∠1=∠2.理由如下:
在△ADC和△AEB中,
AD=AE,
∠ADC=∠AEB,
B D
E
DC=EB,
∴.△ADC≌△AEB(SAS),
.∠DAC=∠EAB,
.∠EAB-∠DAE=∠DAC-∠DAE,
.∠1=∠2.
2.如图,D是△ABC的边AB上一点,DF交AC于
点E,DE=FE,FC∥AB.求证:AE=CE.
证明:.FC∥AB,
∴.∠ADE=∠F.
在△ADE和△CFE中,
(∠ADE=∠F,
B
DE=FE,
∠AED=∠CEF,
∴.△ADE≌△CFE(ASA),
∴.AE=CE.
类型②综合类(需证两次全等)
3.如图,已知∠ABD=∠ACD=90°,BD=CD.
求证:AD⊥BC
证明:在Rt△ABD和Rt△ACD中,
BD=CD,
AD-AD,
E
'.Rt△ABD≌Rt△ACD(HI),
D
∴.∠BDE=∠CDE
BD=CD,
在△BDE和△CDE中,∠BDE=∠CDE,
DE=DE,
∴.△BDE≌△CDE(SAS),∴.∠DEB=∠DEC.
又∠DEB+∠DEC=180°,
∴.∠DEB=∠DEC=90°,∴.AD⊥BC.
4.如图,点A,E,F,C在一条直线上,且AE=CF,分
别过点E,F作DE⊥AC,BF⊥AC,垂足分别为E,
F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG
相等吗?请说明理由;
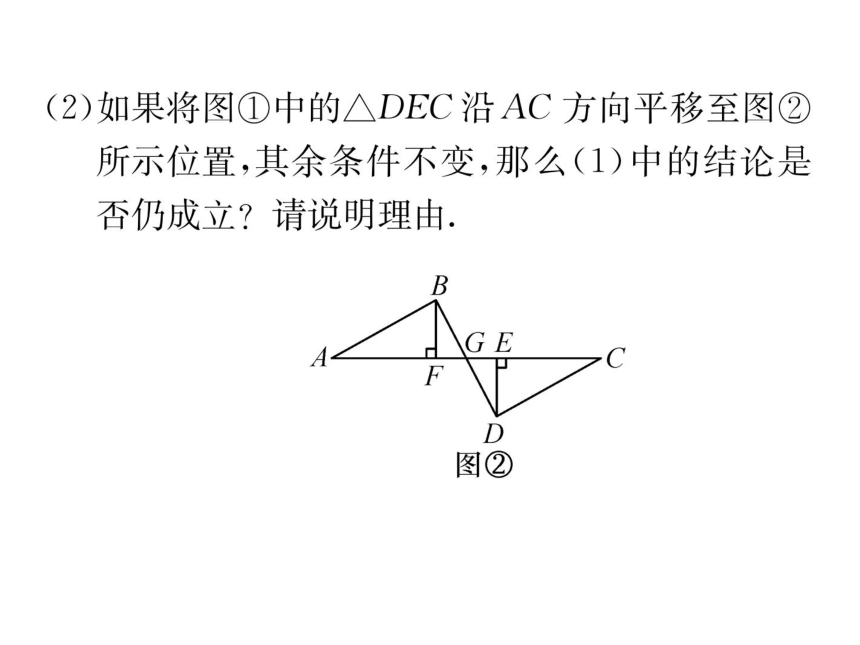
(2)如果将图①中的△DEC沿AC方向平移至图②
所示位置,其余条件不变,那么(1)中的结论是
否仍成立?请说明理由,
B
D
D
图①
图②
解:(1)EG=FG.
理由如下:AE=CF,
.'.AE+EF=CF+EF,AF=CE.
又.BF⊥AC,DE⊥AC,∴.∠BFA=∠DEC=90°.
(AF=CE,
在R△ABF和Rt△CDE中,AB=CD,
∴.Rt△ABF≌Rt△CDE(HL),.∴.BF=DE.
(∠DEG=∠BFG,
在△DEG和△BFG中,∠DGE=∠BGF,
DE=BF,
.△DEG≌△BFG(AAS),∴.EG=FG;
(2)成立,仍有EG=FG.
理由如下:.∵AE=CF,
.'.AE-EF=CF-EF,AF=CE.
以下推理过程同(1),故仍有EG=FG.
类型③探究类(一线三等角模型)
5.如图,已知AB=12cm,CA⊥AB于点A,DB⊥AB
于点B,且AC=4cm,点P从点B向点A运动,每
秒钟走1cm,点Q从点B向点D运动,每秒钟走
2cm,P,Q两点同时出发,运动几秒钟后,△CPA
与△PQB全等?
解:①当△CPA≌△PQB时,BP=
D
AC=4cm,则BQ=AP=AB一
Q
BP=12-4=8(cm),
则点P的运动时间是4÷1=4(s),
力
B
点Q的运动时间是8÷2=4(s),
∴.当运动4s后,△CPA与△PQB全等;
类型①基础类(证一次全等)
1.如图,D,E是△ABC的边BC上的点,AD=AE,
∠ADC=∠AEB,EB=DC,那么∠1和∠2之间是
什么关系?请说出你的理由,
解:∠1=∠2.理由如下:
在△ADC和△AEB中,
AD=AE,
∠ADC=∠AEB,
B D
E
DC=EB,
∴.△ADC≌△AEB(SAS),
.∠DAC=∠EAB,
.∠EAB-∠DAE=∠DAC-∠DAE,
.∠1=∠2.
2.如图,D是△ABC的边AB上一点,DF交AC于
点E,DE=FE,FC∥AB.求证:AE=CE.
证明:.FC∥AB,
∴.∠ADE=∠F.
在△ADE和△CFE中,
(∠ADE=∠F,
B
DE=FE,
∠AED=∠CEF,
∴.△ADE≌△CFE(ASA),
∴.AE=CE.
类型②综合类(需证两次全等)
3.如图,已知∠ABD=∠ACD=90°,BD=CD.
求证:AD⊥BC
证明:在Rt△ABD和Rt△ACD中,
BD=CD,
AD-AD,
E
'.Rt△ABD≌Rt△ACD(HI),
D
∴.∠BDE=∠CDE
BD=CD,
在△BDE和△CDE中,∠BDE=∠CDE,
DE=DE,
∴.△BDE≌△CDE(SAS),∴.∠DEB=∠DEC.
又∠DEB+∠DEC=180°,
∴.∠DEB=∠DEC=90°,∴.AD⊥BC.
4.如图,点A,E,F,C在一条直线上,且AE=CF,分
别过点E,F作DE⊥AC,BF⊥AC,垂足分别为E,
F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG
相等吗?请说明理由;
(2)如果将图①中的△DEC沿AC方向平移至图②
所示位置,其余条件不变,那么(1)中的结论是
否仍成立?请说明理由,
B
D
D
图①
图②
解:(1)EG=FG.
理由如下:AE=CF,
.'.AE+EF=CF+EF,AF=CE.
又.BF⊥AC,DE⊥AC,∴.∠BFA=∠DEC=90°.
(AF=CE,
在R△ABF和Rt△CDE中,AB=CD,
∴.Rt△ABF≌Rt△CDE(HL),.∴.BF=DE.
(∠DEG=∠BFG,
在△DEG和△BFG中,∠DGE=∠BGF,
DE=BF,
.△DEG≌△BFG(AAS),∴.EG=FG;
(2)成立,仍有EG=FG.
理由如下:.∵AE=CF,
.'.AE-EF=CF-EF,AF=CE.
以下推理过程同(1),故仍有EG=FG.
类型③探究类(一线三等角模型)
5.如图,已知AB=12cm,CA⊥AB于点A,DB⊥AB
于点B,且AC=4cm,点P从点B向点A运动,每
秒钟走1cm,点Q从点B向点D运动,每秒钟走
2cm,P,Q两点同时出发,运动几秒钟后,△CPA
与△PQB全等?
解:①当△CPA≌△PQB时,BP=
D
AC=4cm,则BQ=AP=AB一
Q
BP=12-4=8(cm),
则点P的运动时间是4÷1=4(s),
力
B
点Q的运动时间是8÷2=4(s),
∴.当运动4s后,△CPA与△PQB全等;
