12.3 第1课时 角的平分线的性质 复习课件(16张PPT)
文档属性
| 名称 | 12.3 第1课时 角的平分线的性质 复习课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 18:00:15 | ||
图片预览





文档简介
(共16张PPT)
知识构建@
例题引路
知识构建
把一个角分成
定义
角平分线
两个相等的
性质
角的射线
角平分线上的点到角
的两边的距离相等
例题引路
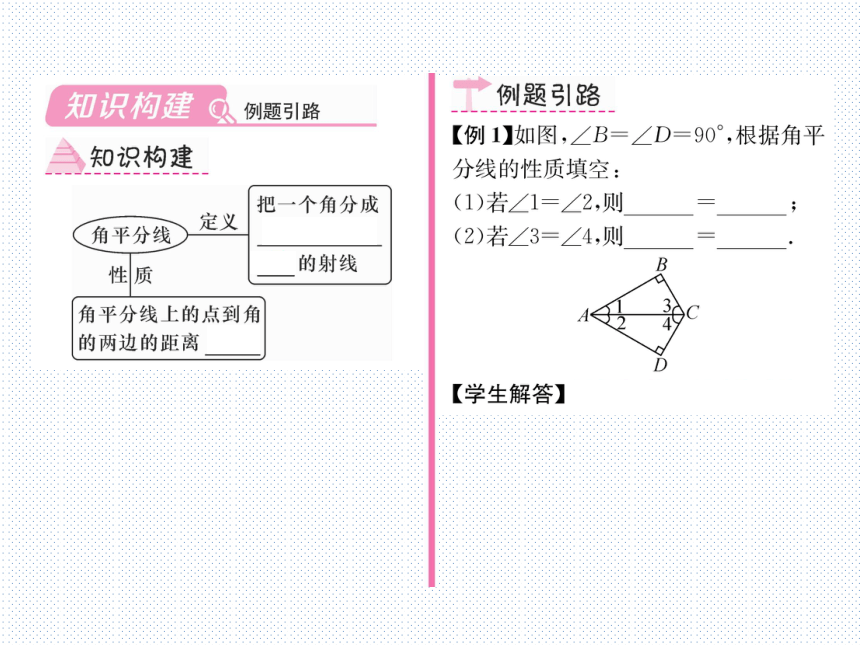
【例1】如图,∠B=∠D=90°,根据角平
分线的性质填空:
(1)若∠1=∠2,则
(2)若∠3=∠4,则
B
学生解答】(1)BC;CD;(2)AB;AD
【例2】如图,BD为∠ABC的平分线,
AB=BC,点P在BD
上,PM⊥AD于点M,
PN⊥CD于点N.
B
求证:PM=PN.
【学生解答】证明:.'BD为∠ABC的
平分线,
∴.∠ABD=∠CBD.
在△ABD和△CBD中,
(AB=CB,
∠ABD=∠CBD,
BD=BD,
∴.△ABD≌△CBD(SAS),
.∠ADB=∠CDB,
即DP为∠ADC的平分线.
又.PMAD,PNCD,
∴.PM=PN.
基础过关
逐点击破
知识点①角的平分线的概念及性质
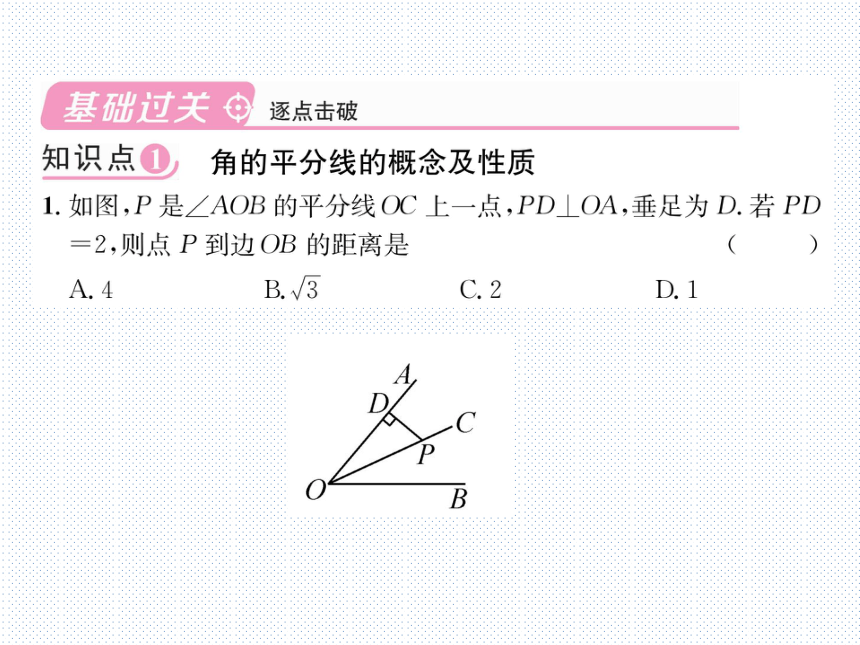
1.如图,P是∠AOB的平分线OC上一点,PD⊥OA,垂足为D.若PD
=2,则点P到边OB的距离是
(C)
A.4
B.√3
C.2
D.1
p
B
(第1题图)
(第2题图)
(第3题图)
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
∠AOC=∠BOC的依据是
(A)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
3.(2020·湘潭中考)如图,点P是∠AO℃的角平分线上一点,PD1
OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最
小值为3
知识点②角的平分线性质的运用
4.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题
意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小
明同学根据题意画出的图形,并写出了不完整的已知和求证
已知:如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD=PE
请你补全已知和求证,并写出证明过程.
证明:.PD⊥OA,PE⊥OB,
∴.∠PDO=∠PEO=90°.
(∠PDO=∠PEO,
在△PDO和△PEO中,∠DOP=∠EOP,
OP=OP,
.∴.△PDO≌△PEO(AAS),
∴.PD=PE
易错点不能综合运用角的平分线的性质和全等三角形的
性质而漏解
5.如图,点P是∠BAC的平分线上的一点,PE⊥AB于
B
点E,PF⊥AC于点F,有以下结论:①PE=PF;
②AE=AF;③∠APE=∠APF.其中正确的是①②
③.(填序号)
知识构建@
例题引路
知识构建
把一个角分成
定义
角平分线
两个相等的
性质
角的射线
角平分线上的点到角
的两边的距离相等
例题引路
【例1】如图,∠B=∠D=90°,根据角平
分线的性质填空:
(1)若∠1=∠2,则
(2)若∠3=∠4,则
B
学生解答】(1)BC;CD;(2)AB;AD
【例2】如图,BD为∠ABC的平分线,
AB=BC,点P在BD
上,PM⊥AD于点M,
PN⊥CD于点N.
B
求证:PM=PN.
【学生解答】证明:.'BD为∠ABC的
平分线,
∴.∠ABD=∠CBD.
在△ABD和△CBD中,
(AB=CB,
∠ABD=∠CBD,
BD=BD,
∴.△ABD≌△CBD(SAS),
.∠ADB=∠CDB,
即DP为∠ADC的平分线.
又.PMAD,PNCD,
∴.PM=PN.
基础过关
逐点击破
知识点①角的平分线的概念及性质
1.如图,P是∠AOB的平分线OC上一点,PD⊥OA,垂足为D.若PD
=2,则点P到边OB的距离是
(C)
A.4
B.√3
C.2
D.1
p
B
(第1题图)
(第2题图)
(第3题图)
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
∠AOC=∠BOC的依据是
(A)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
3.(2020·湘潭中考)如图,点P是∠AO℃的角平分线上一点,PD1
OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最
小值为3
知识点②角的平分线性质的运用
4.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题
意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小
明同学根据题意画出的图形,并写出了不完整的已知和求证
已知:如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD=PE
请你补全已知和求证,并写出证明过程.
证明:.PD⊥OA,PE⊥OB,
∴.∠PDO=∠PEO=90°.
(∠PDO=∠PEO,
在△PDO和△PEO中,∠DOP=∠EOP,
OP=OP,
.∴.△PDO≌△PEO(AAS),
∴.PD=PE
易错点不能综合运用角的平分线的性质和全等三角形的
性质而漏解
5.如图,点P是∠BAC的平分线上的一点,PE⊥AB于
B
点E,PF⊥AC于点F,有以下结论:①PE=PF;
②AE=AF;③∠APE=∠APF.其中正确的是①②
③.(填序号)
