12.2 第4课时 用”HL“判定直角三角形全等 复习课件(18张PPT)
文档属性
| 名称 | 12.2 第4课时 用”HL“判定直角三角形全等 复习课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 14:53:46 | ||
图片预览



文档简介
(共18张PPT)
知识构建
父例题引路
知识构建
直角三角形全等的判定
HL
斜边和一条直角
SSS,SAS.
ASA.AAS
边分别相等的两
个直角三角形全等
广例题引路
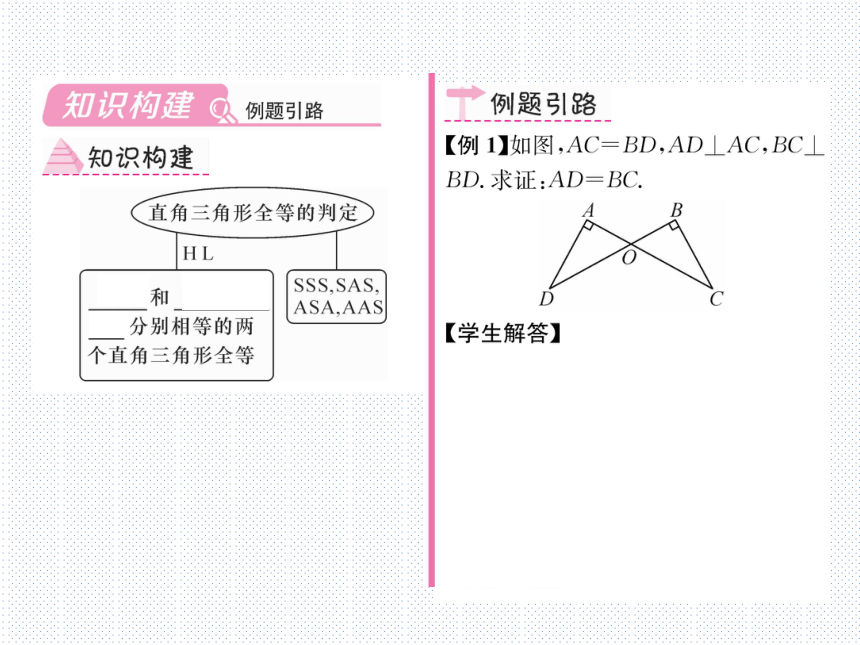
【例1】如图,AC=BD,AD⊥AC,BC
BD.求证:AD=BC
【学生解答】证明:连接CD.
.'ADAC,BC⊥BD,
.∠A=∠B=90°.
在Rt△ADC和Rt△BCD中,
(AC=BD,
DC=CD,
.'.Rt△ADC≌Rt△BCD(HL),
.'.AD=BC.
【例2】下列命题:①两直角边对应相等
的两个直角三角形全等;②两锐角对应
相等的两个直角三角形全等;③斜边和
一直角边对应相等的两个直角三角形
全等;④一锐角和一直角边对应相等的
两个直角三角形全等;⑤一锐角和斜边
对应相等的两个直角三角形全等.其
中,正确的命题是
.(填序号)
【名师点拨】直角三角形是特殊的三角
形.直角三角形全等除了用“HL”外,还
可以用一般三角形全等的判定方法
【学生解答】①③④⑤
A
B
O
D
C
狂站
基础过关 逐点击破
HL定理的内容
知识点①
用“HL”判定直角三角形全等
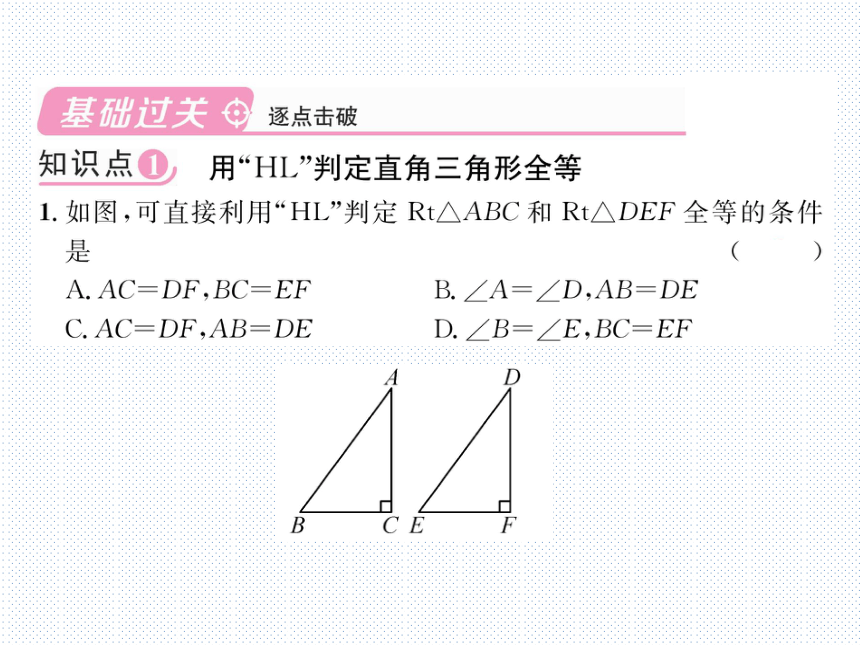
1.如图,可直接利用“HL”判定Rt△ABC和Rt△DEF全等的条件
是
(C)
A.AC-DF,BC=EF
B.∠A=∠D,AB=DE
C.AC=DF,AB-DE
D.∠B=∠E,BC=EF
B
B
E
P
F
-C
CE
(第1题图)
(第2题图)
(第3题图)
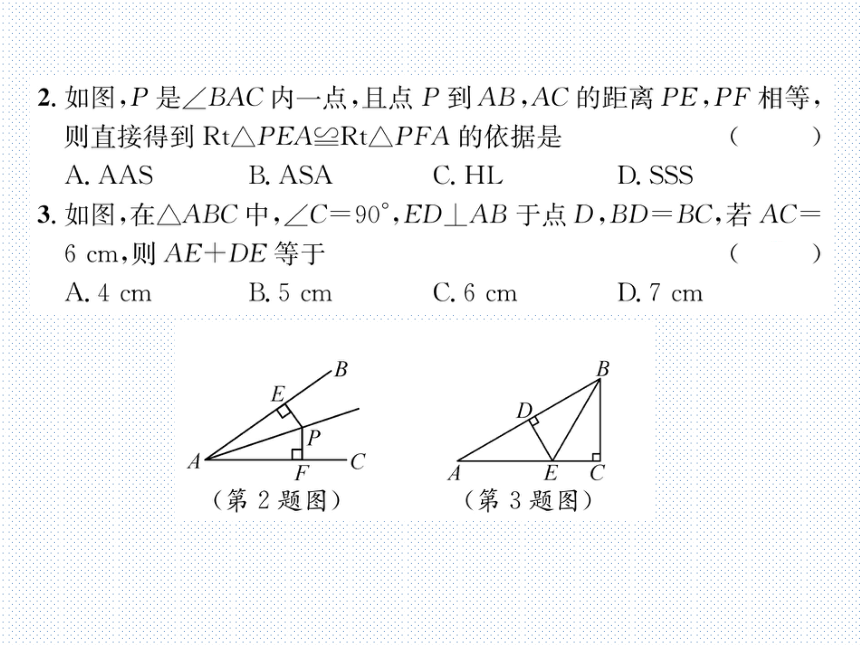
2.如图,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,
则直接得到Rt△PEA≌Rt△PFA的依据是
(C)
A.AAS
B.ASA
C.HI
D.SSS
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=
6cm,则AE十DE等于
(C)
A.4 cm
B.5 cm
C.6 cm
D.7 cm
知识点②直角三角形全等的判定方法
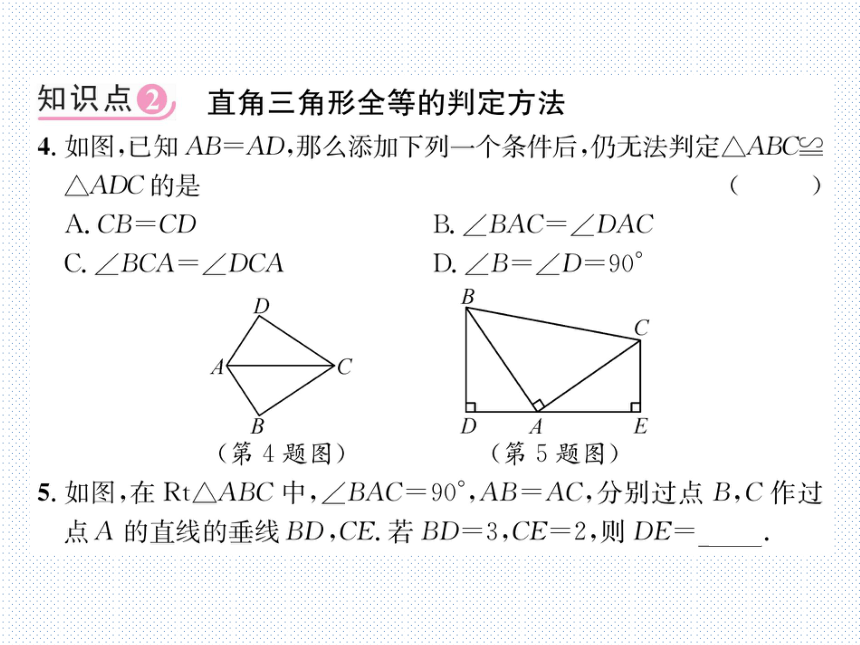
4.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌
△ADC的是
(C)
A.CB-CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
B
B
D
A
(第4题图)
(第5题图)
5.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过
点A的直线的垂线BD,CE.若BD=3,CE=2,则DE=5
易错点用“斜边、直角边”证明全等时不指出是直角三角形
而致错
6.(教材P3练习T2变式)如图,AB=CD,DE⊥AC,BF⊥AC,点E,F
是垂足,AE=CF.求证:BF=DE
证明:.DE⊥AC,BF⊥AC,
..∠AFB=∠CED=90°.
又.‘AE=CF,
.'.AE+EF=CF+EF,AF=CE.
在Rt△AFB和Rt△CED中,
(AB=CD,
AF=CE,
.Rt△AFB≌Rt△CED(HL),
∴.BF=DE
知识构建
父例题引路
知识构建
直角三角形全等的判定
HL
斜边和一条直角
SSS,SAS.
ASA.AAS
边分别相等的两
个直角三角形全等
广例题引路
【例1】如图,AC=BD,AD⊥AC,BC
BD.求证:AD=BC
【学生解答】证明:连接CD.
.'ADAC,BC⊥BD,
.∠A=∠B=90°.
在Rt△ADC和Rt△BCD中,
(AC=BD,
DC=CD,
.'.Rt△ADC≌Rt△BCD(HL),
.'.AD=BC.
【例2】下列命题:①两直角边对应相等
的两个直角三角形全等;②两锐角对应
相等的两个直角三角形全等;③斜边和
一直角边对应相等的两个直角三角形
全等;④一锐角和一直角边对应相等的
两个直角三角形全等;⑤一锐角和斜边
对应相等的两个直角三角形全等.其
中,正确的命题是
.(填序号)
【名师点拨】直角三角形是特殊的三角
形.直角三角形全等除了用“HL”外,还
可以用一般三角形全等的判定方法
【学生解答】①③④⑤
A
B
O
D
C
狂站
基础过关 逐点击破
HL定理的内容
知识点①
用“HL”判定直角三角形全等
1.如图,可直接利用“HL”判定Rt△ABC和Rt△DEF全等的条件
是
(C)
A.AC-DF,BC=EF
B.∠A=∠D,AB=DE
C.AC=DF,AB-DE
D.∠B=∠E,BC=EF
B
B
E
P
F
-C
CE
(第1题图)
(第2题图)
(第3题图)
2.如图,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,
则直接得到Rt△PEA≌Rt△PFA的依据是
(C)
A.AAS
B.ASA
C.HI
D.SSS
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=
6cm,则AE十DE等于
(C)
A.4 cm
B.5 cm
C.6 cm
D.7 cm
知识点②直角三角形全等的判定方法
4.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌
△ADC的是
(C)
A.CB-CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
B
B
D
A
(第4题图)
(第5题图)
5.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过
点A的直线的垂线BD,CE.若BD=3,CE=2,则DE=5
易错点用“斜边、直角边”证明全等时不指出是直角三角形
而致错
6.(教材P3练习T2变式)如图,AB=CD,DE⊥AC,BF⊥AC,点E,F
是垂足,AE=CF.求证:BF=DE
证明:.DE⊥AC,BF⊥AC,
..∠AFB=∠CED=90°.
又.‘AE=CF,
.'.AE+EF=CF+EF,AF=CE.
在Rt△AFB和Rt△CED中,
(AB=CD,
AF=CE,
.Rt△AFB≌Rt△CED(HL),
∴.BF=DE
