12.2 第2课时 用“SAS”判定三角形全等 复习课件(20张PPT)
文档属性
| 名称 | 12.2 第2课时 用“SAS”判定三角形全等 复习课件(20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 14:51:05 | ||
图片预览



文档简介
(共20张PPT)
知识构建Q例题引路
三知识构建
用“SAS”
两边和它们的
判定三角
夹角分别相等的
形全等
两个三角形全等
例题引路
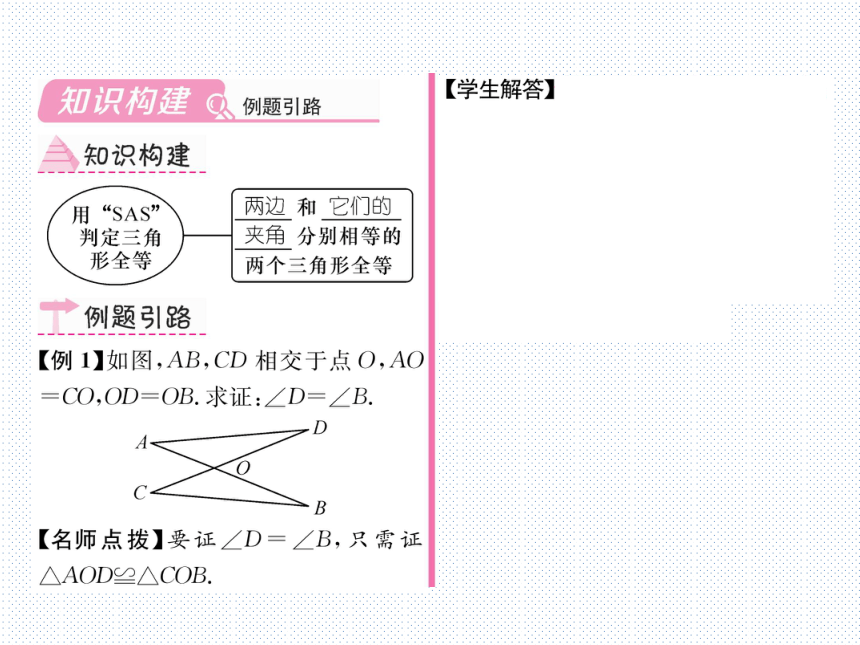
【例1】如图,AB,CD相交于点O,AO
=CO,OD=OB.求证:∠D=∠B.
D
A
B
【名师点拨】要证∠D=∠B,只需证
△AOD≌△COB.
【学生解答】证明:在△AOD和△COB中,
AO-CO,
∠AOD=∠COB,
OD=OB,
.'.△AOD≌△COB(SAS),
.∠D=∠B.
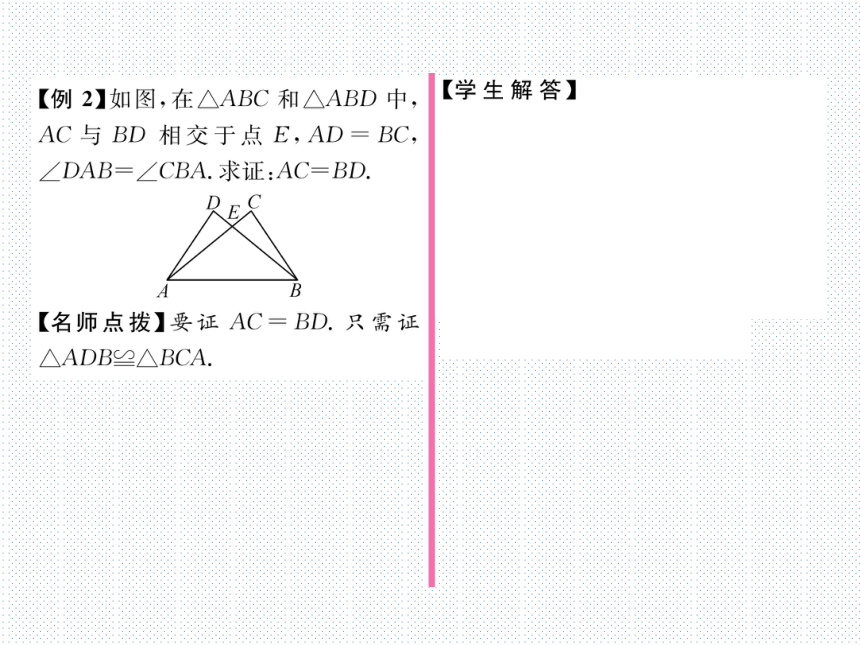
【例2】如图,在△ABC和△ABD中,
AC与BD相交于点E,AD=BC,
∠DAB=∠CBA.求证:AC=BD
【名师点拨】要证AC=BD.只需证
∧ADB2∧BCA.
【学生解答】证明:在△ADB中和
△BCA中,
AD=BC,
∠DAB=∠CBA,
AB=BA,
.'.△ADB≌△BCA(SAS),
.'.AC=BD.
还站
基础过关电
逐点击破
SAS定理
知识点用“SAS”判定三角形全等
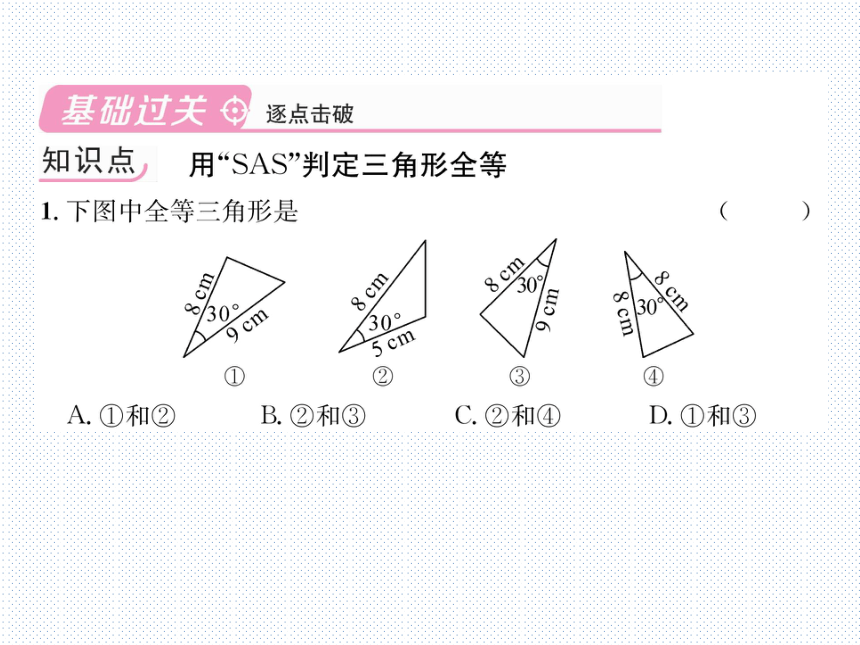
1.下图中全等三角形是
(D
30
∞30%
8 cm
cm
30
5cm
①
②
③
④
A.①和②
B.②和③
C.②和④
D.①和③
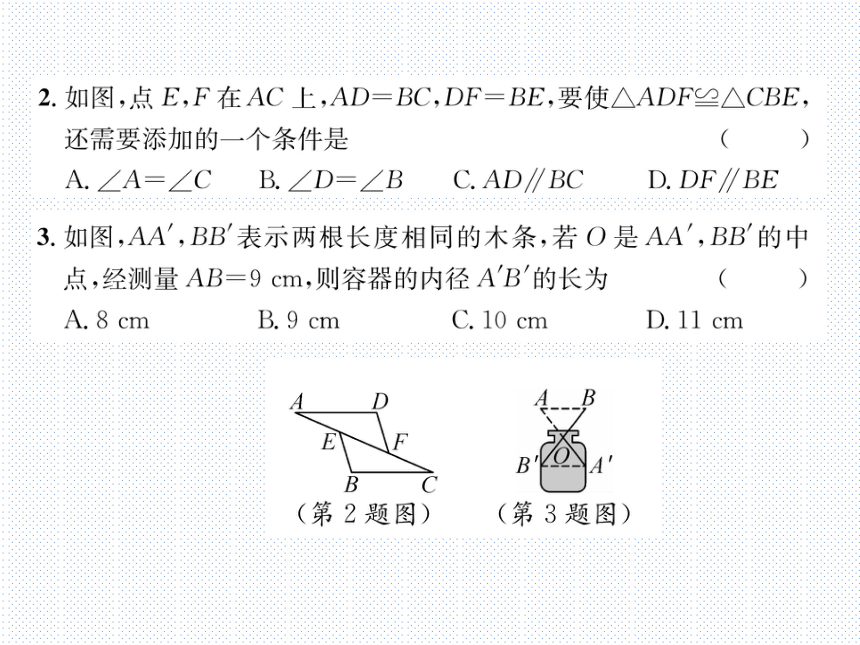
2.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,
还需要添加的一个条件是
(B)
A.∠A=∠C
B.∠D=∠B
C.AD∥BC
D.DF∥BE
B
(第2题图)
(第3题图)
(第4题图)
(第5题图)
3.如图,AA',BB表示两根长度相同的木条,若O是AA',BB的中
点,经测量AB=9cm,则容器的内径A'B'的长为
(B)
A.8 cm
B.9 cm
C.10 cm
D,11 cm
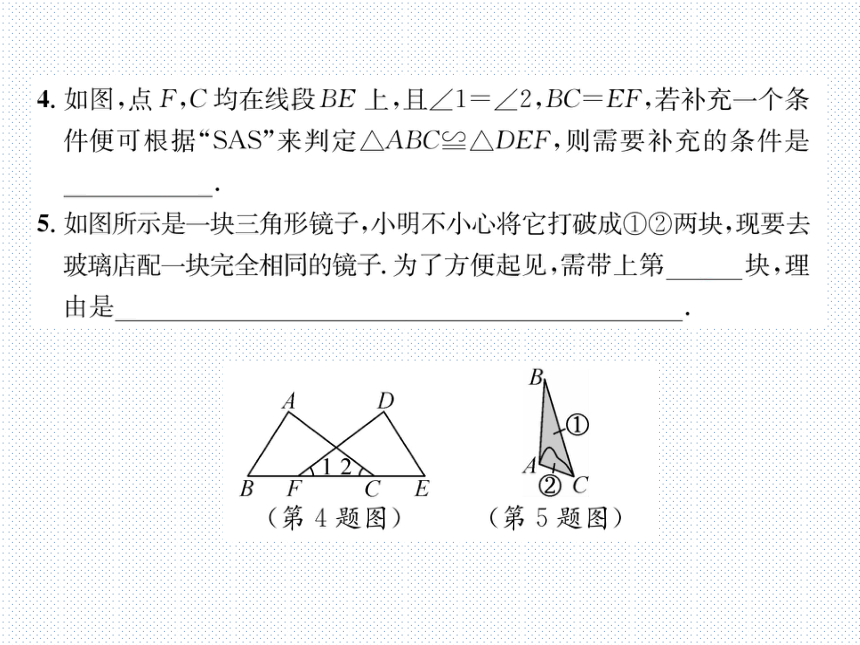
4.如图,点F,C均在线段BE上,且∠1=∠2,BC=EF,若补充一个条
件便可根据“SAS”来判定△ABC≌△DEF,侧需要补充的条件是
AC=DF
5.如图所示是一块三角形镜子,小明不小心将它打破成①②两块,现要去
玻璃店配一块完全相同的镜子.为了方便起见,需带上第①块,理
由是两边和它们的夹角分别相等的两个三角形全等·
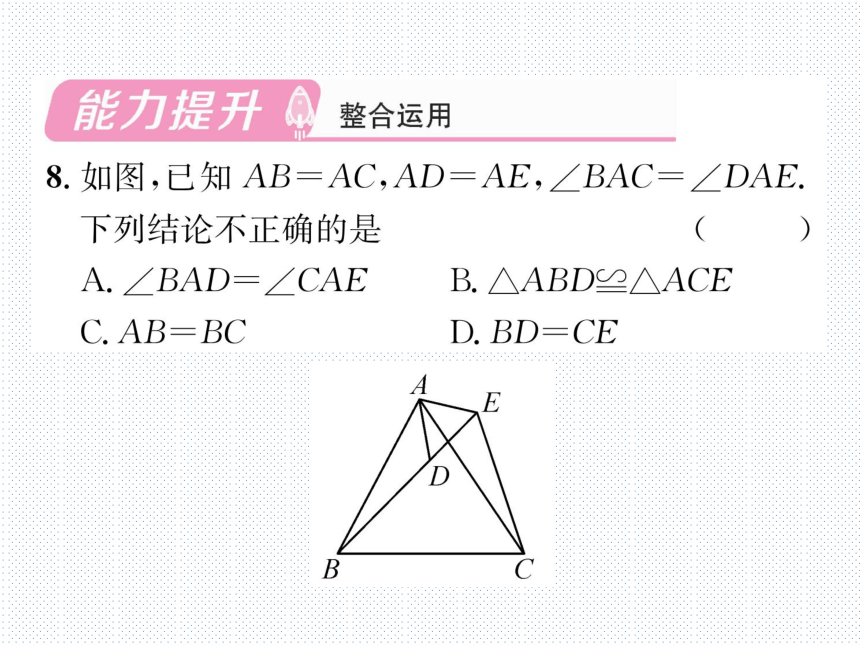
6.(2020·吉林中考)如图,在△ABC中,AB>AC,点D在边AB上,
且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB
同侧,连接BE.求证:△DEB≌△ABC.
证明:.DE∥AC,
∴.∠EDB=∠A.
DE-AB.
在△DEB和△ABC中,
∠EDB=∠A,
BD=CA,
∴.△DEB2△ABC(SAS).
知识构建Q例题引路
三知识构建
用“SAS”
两边和它们的
判定三角
夹角分别相等的
形全等
两个三角形全等
例题引路
【例1】如图,AB,CD相交于点O,AO
=CO,OD=OB.求证:∠D=∠B.
D
A
B
【名师点拨】要证∠D=∠B,只需证
△AOD≌△COB.
【学生解答】证明:在△AOD和△COB中,
AO-CO,
∠AOD=∠COB,
OD=OB,
.'.△AOD≌△COB(SAS),
.∠D=∠B.
【例2】如图,在△ABC和△ABD中,
AC与BD相交于点E,AD=BC,
∠DAB=∠CBA.求证:AC=BD
【名师点拨】要证AC=BD.只需证
∧ADB2∧BCA.
【学生解答】证明:在△ADB中和
△BCA中,
AD=BC,
∠DAB=∠CBA,
AB=BA,
.'.△ADB≌△BCA(SAS),
.'.AC=BD.
还站
基础过关电
逐点击破
SAS定理
知识点用“SAS”判定三角形全等
1.下图中全等三角形是
(D
30
∞30%
8 cm
cm
30
5cm
①
②
③
④
A.①和②
B.②和③
C.②和④
D.①和③
2.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,
还需要添加的一个条件是
(B)
A.∠A=∠C
B.∠D=∠B
C.AD∥BC
D.DF∥BE
B
(第2题图)
(第3题图)
(第4题图)
(第5题图)
3.如图,AA',BB表示两根长度相同的木条,若O是AA',BB的中
点,经测量AB=9cm,则容器的内径A'B'的长为
(B)
A.8 cm
B.9 cm
C.10 cm
D,11 cm
4.如图,点F,C均在线段BE上,且∠1=∠2,BC=EF,若补充一个条
件便可根据“SAS”来判定△ABC≌△DEF,侧需要补充的条件是
AC=DF
5.如图所示是一块三角形镜子,小明不小心将它打破成①②两块,现要去
玻璃店配一块完全相同的镜子.为了方便起见,需带上第①块,理
由是两边和它们的夹角分别相等的两个三角形全等·
6.(2020·吉林中考)如图,在△ABC中,AB>AC,点D在边AB上,
且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB
同侧,连接BE.求证:△DEB≌△ABC.
证明:.DE∥AC,
∴.∠EDB=∠A.
DE-AB.
在△DEB和△ABC中,
∠EDB=∠A,
BD=CA,
∴.△DEB2△ABC(SAS).
