课题§16.3分式方程[下学期]
文档属性
| 名称 | 课题§16.3分式方程[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 32.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-23 19:18:00 | ||
图片预览





文档简介
课件12张PPT。中沟初中公开课
课题:§16.3分式方程
授课人:刘后贵回顾旧知: 1.我们已经学过那些方程?是怎样的方程?如何求解?
⑴前面我们学过了一元一次方程.
⑵一元一次方程是整式方程.
⑶解一元一次方程的步骤是①去分母②去括号③移项④合并同类项⑤系数化为1. 2.一艘轮船在静水中的最大航行速度为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航行逆流航行60千米所用时间相等,江水的流速是多少?
解:设江水流速为v千米/时,由题意得:解:去分母:方程两边都乘以最简公分母(20+v)(20-v)得:
100(20-v)=60(20-v) ②
解得:v=5①问题1:
⑴ 是我们以前所学的整式方程吗?
分式方程:分母中含有字母的方程叫分式方程.
⑵如何解分式方程呢?
应用数学化归思想,可通过“去分母”将分式方程转化为整式方程.
观察方程①、②中的v的取值范围相同吗?问题2:
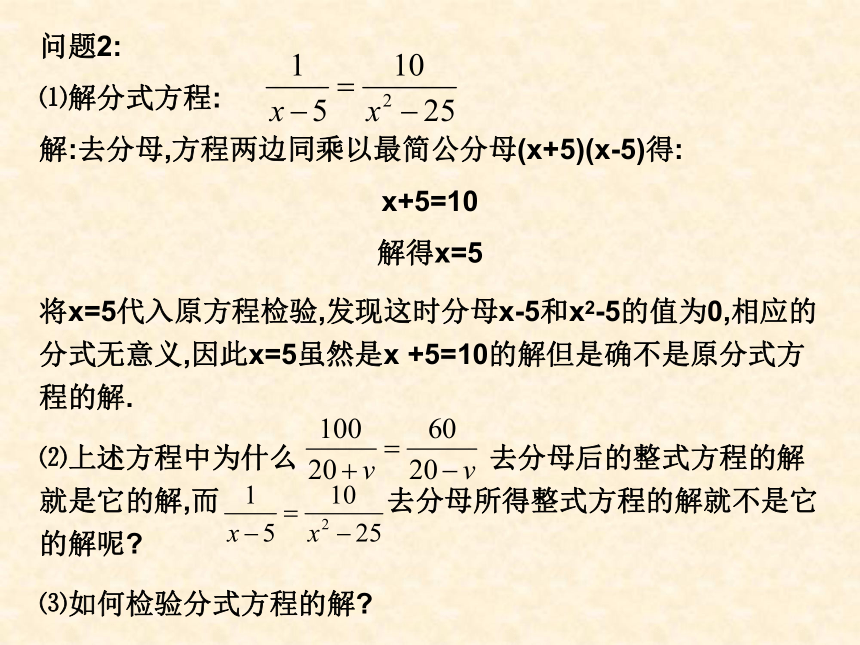
⑴解分式方程:
解:去分母,方程两边同乘以最简公分母(x+5)(x-5)得:
x+5=10
解得x=5
将x=5代入原方程检验,发现这时分母x-5和x2-5的值为0,相应的分式无意义,因此x=5虽然是x +5=10的解但是确不是原分式方程的解.
⑵上述方程中为什么 去分母后的整式方程的解就是它的解,而 去分母所得整式方程的解就不是它的解呢?
⑶如何检验分式方程的解? 明确:
解分式方程去分母时,方程的两边要同时乘一个含未知数的式子(最简公分母).方程 两边同乘(20+v)(20-v),得到的整式方程并进而得到它的解v=5.当v=5时, (20+v)(20-v)≠0,这就是说,为了去分母,分式方程两边同乘了一个不为0的式子,因此所得整式方程与原分式方程的解相同.
而方程 两边同乘(x+5)(x-5),得到整式方程并进而得到它的解x=5.当x=5时,(x+5)(x-5)=0,这就是说,为去分母,原分式方程两边同乘了一个等于0的式子,这时所得整式方程的解使原分式方程出现分母为0的现象,因此这样的解不是原分式方程的解,称为增根.课堂演练:
解下列分式方程:解:⑴方程两边同乘x(x-3),得:
2x=3x-9
解得
x=9
检验:x=9时, x(x-3) ≠0,9是原分式方程得根.
⑵方程两边同乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3
解得
x=1
检验: x=1时, (x-1)(x+2)=0,1不是原分式方程得解,原分式方程无解.
归纳:
1.解分式方程的关键是如何将分式方程转化整式方程来解,转化的方法是在方程两边都乘以最简公分母,从而去掉分母.
2.由于转化的过程中同乘了含有未知数的一个整式,因而可能使未知数的取值范围扩大,容易造成增根,所以解分式方程一定要验根.
3.验根的方法是把整式方程的根代入最简公分母,看结果是否为零,使最简公分母为零的根是原方程的根必须舍去.课堂练习:
1.解分式方程:
2. .有两块面积相同的小麦试验田,第一块使用原品种,第二块使用新品种,分别收取小麦9000kg和15000kg,已知第一块试验田每公顷的产量比第二块少3000kg,分别求这两块试验田每公顷的产量.课堂总结:
1.解分式方程的基本思路,就是把分式方程转化为整式方程,即把方程的两边同时乘以各分母的最简公分母,从而约去分母,化为整式方程,然后再解整式方程.
2.解分式方程的一般步骤:
⑴在方程的两边都乘以最简公分母,约去分母,化为整式方程;⑵解这个整式方程⑶验根.
用一个整式去乘分式方程的两边时,有可能出现增根,因此要验根,验根方法有两种:
⑴代入原分式方程检验
⑵代入所乘的整式(最简公分母)检验它的值是否为零,如果不为零就是根,否则就是增根.作业:
课本:P38
习题16.3 1.⑴⑶⑸⑺ 2. ⑴谢谢!
课题:§16.3分式方程
授课人:刘后贵回顾旧知: 1.我们已经学过那些方程?是怎样的方程?如何求解?
⑴前面我们学过了一元一次方程.
⑵一元一次方程是整式方程.
⑶解一元一次方程的步骤是①去分母②去括号③移项④合并同类项⑤系数化为1. 2.一艘轮船在静水中的最大航行速度为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航行逆流航行60千米所用时间相等,江水的流速是多少?
解:设江水流速为v千米/时,由题意得:解:去分母:方程两边都乘以最简公分母(20+v)(20-v)得:
100(20-v)=60(20-v) ②
解得:v=5①问题1:
⑴ 是我们以前所学的整式方程吗?
分式方程:分母中含有字母的方程叫分式方程.
⑵如何解分式方程呢?
应用数学化归思想,可通过“去分母”将分式方程转化为整式方程.
观察方程①、②中的v的取值范围相同吗?问题2:
⑴解分式方程:
解:去分母,方程两边同乘以最简公分母(x+5)(x-5)得:
x+5=10
解得x=5
将x=5代入原方程检验,发现这时分母x-5和x2-5的值为0,相应的分式无意义,因此x=5虽然是x +5=10的解但是确不是原分式方程的解.
⑵上述方程中为什么 去分母后的整式方程的解就是它的解,而 去分母所得整式方程的解就不是它的解呢?
⑶如何检验分式方程的解? 明确:
解分式方程去分母时,方程的两边要同时乘一个含未知数的式子(最简公分母).方程 两边同乘(20+v)(20-v),得到的整式方程并进而得到它的解v=5.当v=5时, (20+v)(20-v)≠0,这就是说,为了去分母,分式方程两边同乘了一个不为0的式子,因此所得整式方程与原分式方程的解相同.
而方程 两边同乘(x+5)(x-5),得到整式方程并进而得到它的解x=5.当x=5时,(x+5)(x-5)=0,这就是说,为去分母,原分式方程两边同乘了一个等于0的式子,这时所得整式方程的解使原分式方程出现分母为0的现象,因此这样的解不是原分式方程的解,称为增根.课堂演练:
解下列分式方程:解:⑴方程两边同乘x(x-3),得:
2x=3x-9
解得
x=9
检验:x=9时, x(x-3) ≠0,9是原分式方程得根.
⑵方程两边同乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3
解得
x=1
检验: x=1时, (x-1)(x+2)=0,1不是原分式方程得解,原分式方程无解.
归纳:
1.解分式方程的关键是如何将分式方程转化整式方程来解,转化的方法是在方程两边都乘以最简公分母,从而去掉分母.
2.由于转化的过程中同乘了含有未知数的一个整式,因而可能使未知数的取值范围扩大,容易造成增根,所以解分式方程一定要验根.
3.验根的方法是把整式方程的根代入最简公分母,看结果是否为零,使最简公分母为零的根是原方程的根必须舍去.课堂练习:
1.解分式方程:
2. .有两块面积相同的小麦试验田,第一块使用原品种,第二块使用新品种,分别收取小麦9000kg和15000kg,已知第一块试验田每公顷的产量比第二块少3000kg,分别求这两块试验田每公顷的产量.课堂总结:
1.解分式方程的基本思路,就是把分式方程转化为整式方程,即把方程的两边同时乘以各分母的最简公分母,从而约去分母,化为整式方程,然后再解整式方程.
2.解分式方程的一般步骤:
⑴在方程的两边都乘以最简公分母,约去分母,化为整式方程;⑵解这个整式方程⑶验根.
用一个整式去乘分式方程的两边时,有可能出现增根,因此要验根,验根方法有两种:
⑴代入原分式方程检验
⑵代入所乘的整式(最简公分母)检验它的值是否为零,如果不为零就是根,否则就是增根.作业:
课本:P38
习题16.3 1.⑴⑶⑸⑺ 2. ⑴谢谢!
