2022-2023学年华师大版数学七年级上册 2.4 绝对值 教案
文档属性
| 名称 | 2022-2023学年华师大版数学七年级上册 2.4 绝对值 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 467.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 11:36:06 | ||
图片预览



文档简介
2.4绝对值
教学目标:
1..助数轴初步理解绝对值的概念及表示方法;
2.体会绝对值的作用与意义;
3.能熟练掌握有理数绝对值的求法和有关的简单计算。
教学重难点:
1.重点:正确理解绝对值的概念,能求一个数的绝对值。
2.难点:正确理解绝对值的几何意义和代数意义。
教学过程:
一、创设情境、引入新知
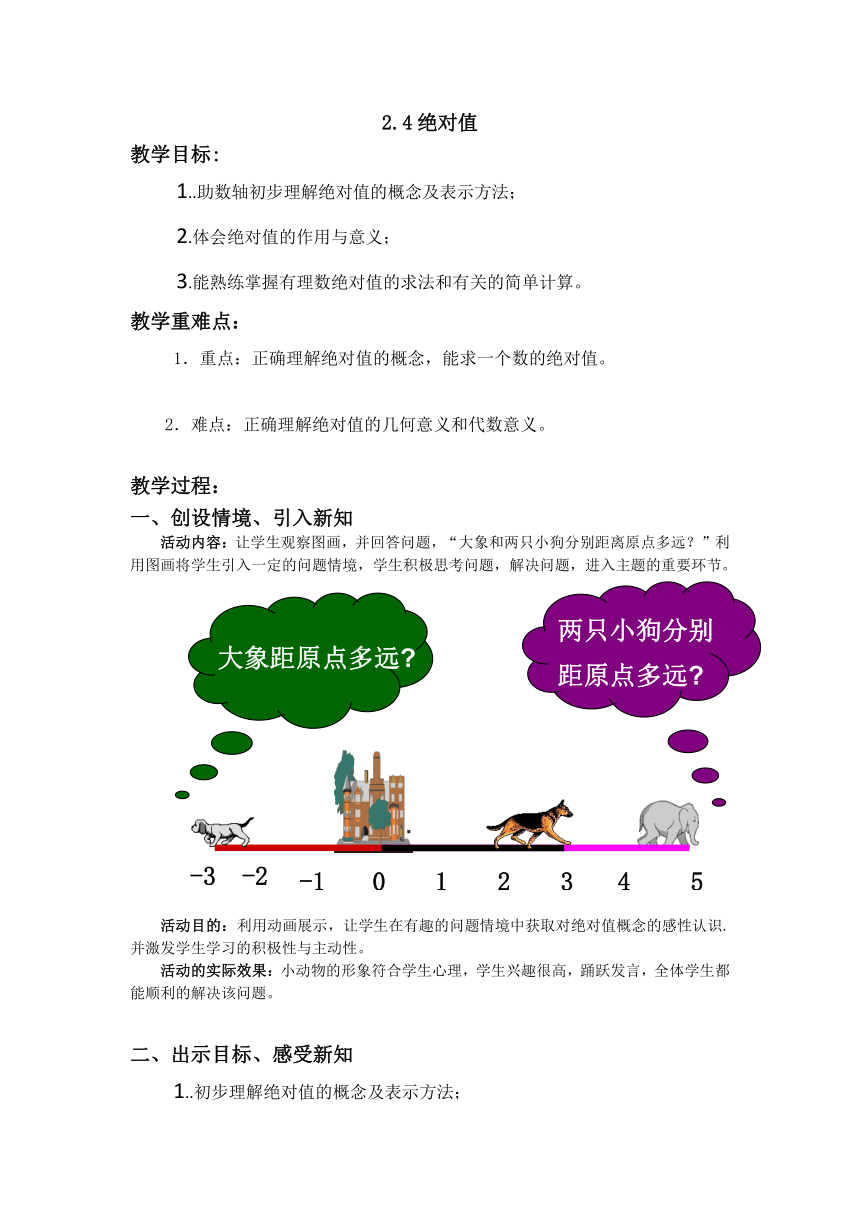
活动内容:让学生观察图画,并回答问题,“大象和两只小狗分别距离原点多远?”利用图画将学生引入一定的问题情境,学生积极思考问题,解决问题,进入主题的重要环节。
活动目的:利用动画展示,让学生在有趣的问题情境中获取对绝对值概念的感性认识.并激发学生学习的积极性与主动性。
活动的实际效果:小动物的形象符合学生心理,学生兴趣很高,踊跃发言,全体学生都能顺利的解决该问题。
二、出示目标、感受新知
1..初步理解绝对值的概念及表示方法;
2.体会绝对值的作用与意义;
3.能熟练掌握有理数绝对值的求法和有关的简单计算。
自学指导、探究新知
我们假设超级玛丽行走时每次都从原点出发。
请问:超级玛丽3次共走了多少路程?
数轴上表示+3的点到原点的距离为( ) ,
所以我们称+3的绝对值为3
数轴上表示-8的点到原点的距离为___,
所以我们称-8的绝对值为8;
数轴上表示+4.5的点到原点的距离为___,
所以我们称+4.5的绝对值为4.5 ;
提出问题
1.什么是一个数的绝对值?
2.怎样用符号表示一个数的绝对值?
试一试
(1)∣-5∣=____ (2)∣-0.5∣ =____
(3)∣+1∣=_____ (4)∣0∣ =_____
游戏规则
数学王国的“有理数们”到公园游玩,在公园的入口处是“绝对值大叔”在值班,他说:“经过我以后,凡是结果为‘正数’的往右走,否则就往左走。”
你带着刚才写的数,在经过“绝对值大叔”后,会走那条路呢?
活动要求:
1. 在发下的另5张小纸条上,每张写一个你喜欢的数,正数、负数、0都可以。
2. 将写好纸条给你的同桌,请他在纸条上求出这些数的绝对值。
3. 请各四人小组把写好的纸条放在一起,排一排,观察一下有什么规律?
畅所欲言
1. 会求一个数的绝对值吗?是怎样求的?
2. 还有什么收获吗?
(1)如何用有理数表示他们的行驶情况
(2)这两个有理数有什么关系?
(3)在数轴上把这两个有理数表示出来。
设计意图:通过提问,复习用有理数表示具有相反意义的量,相反数的意义,在数轴上表示有理数等有关内容,为学习新知识做准备。
(二)交流对话,探究新知
1.引入:
(1)若每辆车行驶每千米耗油0.2升,则甲乙两辆车各耗多少升油?
(2)计算汽车耗油量的过程中,只与什么有关?而与什么无关?
耗油量的计算只与汽车行驶的路程有关,而与方向无关,在实际生活中不注重方向的量还有很多,本节我们将学习一个新的不注重方向的量——绝对值。
2.引导学生从数轴上认识绝对值的几何意义。
师:+6和-6是相反数,它们只有符号不同,它们什么相同呢?
生:思考讨论
师:在数轴上标出到原点距离是6个单位长度的点。
引导学生观察:数轴上表示+6和-6两点,虽然分居在原点的两旁,符号不同,但与原点之间都是相隔6个单位长度。
指出:
在数轴上表示+6和-6的点与原点的距离都是6,我们就说+6的绝对值是6,-6的绝对值也是6。
归纳:
绝对值的几何意义:在数轴上表示数a的点与原点的距离叫做数a的绝对值,记做∣a∣。
3.探究绝对值的代数意义及性质
师:一个正数的绝对值是什么?0的绝对值是什么?负数呢?
生:学生小组交流、讨论,小组代表汇报讨论结论。
师:同学们说的对,但这只是绝对值意义的文字叙述,事实上,这意义还可以用数学式子来表达。大家知道怎样用数学式子来表达吗?
生:学生分组讨论,分析思考,得到三个相应的表达式。
即:
(1)如果a>0,那么│a│=a;
(2)如果a=0,那么│a│=0;
(3)如果a<0,那么│a│=-a。
归纳:非负数的绝对值是它本身,非正数的绝对值是它的相反数。互为相反数的两个数的绝对值相等。
师:不论有理数a取何值,它的绝对值是什么数?
生:正数或0,即∣a∣≧0
归纳:由此可知,不论a取何值,它的绝对值总是正数或0(通常也称为非负数),即对任意有理数a而言,总有:a≧0 。这是一条非常重要的性质,即绝对值的“非负性”。
补充:
(1)绝对值等于0的数只有一个,就是0;
(2)绝对值等于同一个正数的数有两个,这两个数互为相反数;
(3)互为相反数的两个数的绝对值相等。
四、自学反馈、应用新知
1. -5的相反数是______;|-5|=______,不小于-2的负整数是______。
2.若x>0,y<0,求|x-y+2|-|y-x-3|的值。
3.绝对值不大于4的整数有______个。
4.教科书第24页练习1 、2。
五、当堂训练,体验成功
一个数的绝对值是它本身,那么这个数一定是 。
2.绝对值小于3的整数有 个,分别是 。
3.如果一个数的绝对值等于 4,那么这个数等于 。
4.用>、<、=号填空
│-5│ 0 , │+3│ 0,
│+8│ │-8│ , │-5│ │-8│.
5.在数轴上表示下列各数,并求它们的绝对值:
,6 ,-3 , ;
6.比较下列各组数的大小:
(1) (2)
(3) (4)
布置作业:
1.教科书第25页习题第2、3。
板书设计:
绝对值
问题情境
甲乙两辆车从城站火车站同时开出,甲车向东行驶5千米到达一候车亭,乙车向西行驶5千米到达另一候车亭。问:
(1)如何用有理数表示他们的行驶情况
(2)这两个有理数有什么关系?
归纳:
(3)在数轴上把这两个有理数表示出来。
(1)如果a>0,那么│a│=a;
(2)如果a=0,那么│a│=0;
(3)如果a<0,那么│a│=-a。
非负数的绝对值是它本身,非正数的绝对值是它的相反数。互为相反数的两个数的绝对值相等。
教后札记:
0
1
2
3
4
-1
-2
-3
5
大象距原点多远
两只小狗分别
距原点多远
教学目标:
1..助数轴初步理解绝对值的概念及表示方法;
2.体会绝对值的作用与意义;
3.能熟练掌握有理数绝对值的求法和有关的简单计算。
教学重难点:
1.重点:正确理解绝对值的概念,能求一个数的绝对值。
2.难点:正确理解绝对值的几何意义和代数意义。
教学过程:
一、创设情境、引入新知
活动内容:让学生观察图画,并回答问题,“大象和两只小狗分别距离原点多远?”利用图画将学生引入一定的问题情境,学生积极思考问题,解决问题,进入主题的重要环节。
活动目的:利用动画展示,让学生在有趣的问题情境中获取对绝对值概念的感性认识.并激发学生学习的积极性与主动性。
活动的实际效果:小动物的形象符合学生心理,学生兴趣很高,踊跃发言,全体学生都能顺利的解决该问题。
二、出示目标、感受新知
1..初步理解绝对值的概念及表示方法;
2.体会绝对值的作用与意义;
3.能熟练掌握有理数绝对值的求法和有关的简单计算。
自学指导、探究新知
我们假设超级玛丽行走时每次都从原点出发。
请问:超级玛丽3次共走了多少路程?
数轴上表示+3的点到原点的距离为( ) ,
所以我们称+3的绝对值为3
数轴上表示-8的点到原点的距离为___,
所以我们称-8的绝对值为8;
数轴上表示+4.5的点到原点的距离为___,
所以我们称+4.5的绝对值为4.5 ;
提出问题
1.什么是一个数的绝对值?
2.怎样用符号表示一个数的绝对值?
试一试
(1)∣-5∣=____ (2)∣-0.5∣ =____
(3)∣+1∣=_____ (4)∣0∣ =_____
游戏规则
数学王国的“有理数们”到公园游玩,在公园的入口处是“绝对值大叔”在值班,他说:“经过我以后,凡是结果为‘正数’的往右走,否则就往左走。”
你带着刚才写的数,在经过“绝对值大叔”后,会走那条路呢?
活动要求:
1. 在发下的另5张小纸条上,每张写一个你喜欢的数,正数、负数、0都可以。
2. 将写好纸条给你的同桌,请他在纸条上求出这些数的绝对值。
3. 请各四人小组把写好的纸条放在一起,排一排,观察一下有什么规律?
畅所欲言
1. 会求一个数的绝对值吗?是怎样求的?
2. 还有什么收获吗?
(1)如何用有理数表示他们的行驶情况
(2)这两个有理数有什么关系?
(3)在数轴上把这两个有理数表示出来。
设计意图:通过提问,复习用有理数表示具有相反意义的量,相反数的意义,在数轴上表示有理数等有关内容,为学习新知识做准备。
(二)交流对话,探究新知
1.引入:
(1)若每辆车行驶每千米耗油0.2升,则甲乙两辆车各耗多少升油?
(2)计算汽车耗油量的过程中,只与什么有关?而与什么无关?
耗油量的计算只与汽车行驶的路程有关,而与方向无关,在实际生活中不注重方向的量还有很多,本节我们将学习一个新的不注重方向的量——绝对值。
2.引导学生从数轴上认识绝对值的几何意义。
师:+6和-6是相反数,它们只有符号不同,它们什么相同呢?
生:思考讨论
师:在数轴上标出到原点距离是6个单位长度的点。
引导学生观察:数轴上表示+6和-6两点,虽然分居在原点的两旁,符号不同,但与原点之间都是相隔6个单位长度。
指出:
在数轴上表示+6和-6的点与原点的距离都是6,我们就说+6的绝对值是6,-6的绝对值也是6。
归纳:
绝对值的几何意义:在数轴上表示数a的点与原点的距离叫做数a的绝对值,记做∣a∣。
3.探究绝对值的代数意义及性质
师:一个正数的绝对值是什么?0的绝对值是什么?负数呢?
生:学生小组交流、讨论,小组代表汇报讨论结论。
师:同学们说的对,但这只是绝对值意义的文字叙述,事实上,这意义还可以用数学式子来表达。大家知道怎样用数学式子来表达吗?
生:学生分组讨论,分析思考,得到三个相应的表达式。
即:
(1)如果a>0,那么│a│=a;
(2)如果a=0,那么│a│=0;
(3)如果a<0,那么│a│=-a。
归纳:非负数的绝对值是它本身,非正数的绝对值是它的相反数。互为相反数的两个数的绝对值相等。
师:不论有理数a取何值,它的绝对值是什么数?
生:正数或0,即∣a∣≧0
归纳:由此可知,不论a取何值,它的绝对值总是正数或0(通常也称为非负数),即对任意有理数a而言,总有:a≧0 。这是一条非常重要的性质,即绝对值的“非负性”。
补充:
(1)绝对值等于0的数只有一个,就是0;
(2)绝对值等于同一个正数的数有两个,这两个数互为相反数;
(3)互为相反数的两个数的绝对值相等。
四、自学反馈、应用新知
1. -5的相反数是______;|-5|=______,不小于-2的负整数是______。
2.若x>0,y<0,求|x-y+2|-|y-x-3|的值。
3.绝对值不大于4的整数有______个。
4.教科书第24页练习1 、2。
五、当堂训练,体验成功
一个数的绝对值是它本身,那么这个数一定是 。
2.绝对值小于3的整数有 个,分别是 。
3.如果一个数的绝对值等于 4,那么这个数等于 。
4.用>、<、=号填空
│-5│ 0 , │+3│ 0,
│+8│ │-8│ , │-5│ │-8│.
5.在数轴上表示下列各数,并求它们的绝对值:
,6 ,-3 , ;
6.比较下列各组数的大小:
(1) (2)
(3) (4)
布置作业:
1.教科书第25页习题第2、3。
板书设计:
绝对值
问题情境
甲乙两辆车从城站火车站同时开出,甲车向东行驶5千米到达一候车亭,乙车向西行驶5千米到达另一候车亭。问:
(1)如何用有理数表示他们的行驶情况
(2)这两个有理数有什么关系?
归纳:
(3)在数轴上把这两个有理数表示出来。
(1)如果a>0,那么│a│=a;
(2)如果a=0,那么│a│=0;
(3)如果a<0,那么│a│=-a。
非负数的绝对值是它本身,非正数的绝对值是它的相反数。互为相反数的两个数的绝对值相等。
教后札记:
0
1
2
3
4
-1
-2
-3
5
大象距原点多远
两只小狗分别
距原点多远
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
