人教版七年级数学上册 4.2.2线段的比较 课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学上册 4.2.2线段的比较 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
第四章 几何图形初步
4.2 直线、射线、线段
第2课时 线段的比较
1
课堂讲解
尺规作图
线段大小的比较
线段的中点
2
课时流程
逐点
导讲练
课堂小结
课后作业
A
B
图1
b
图2
a
图3
O
A
图4
A
B
图5
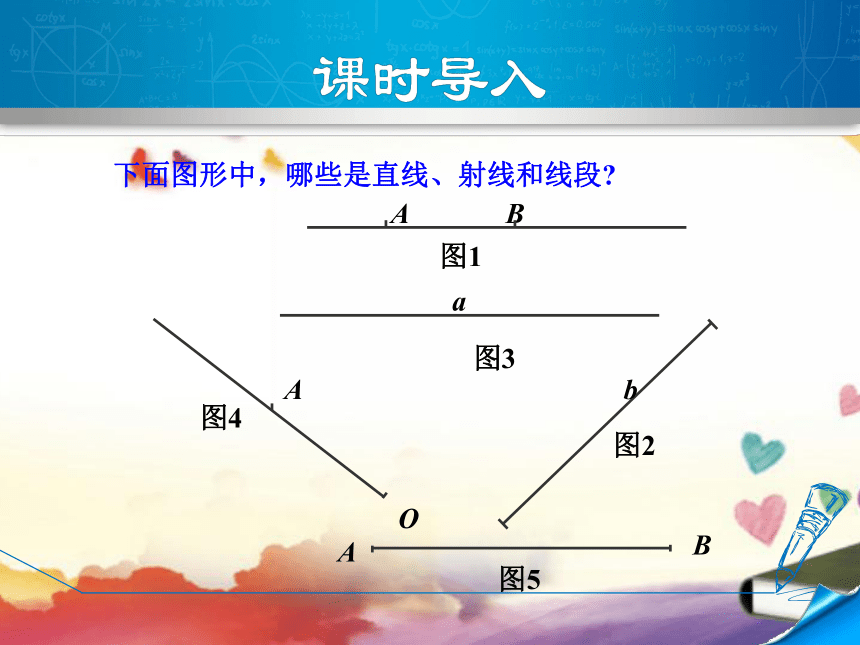
下面图形中,哪些是直线、射线和线段
1
知识点
尺规作图
尺规作图:在数学中,我们常限定用无刻度的直尺
和圆规作图,这就是尺规作图,利用尺规作图可以
将一条线段移到另一条线段上.用直尺(无刻度)和
圆规作一条线段等于已知线段的步骤:
(1)利用直尺(无刻度)作一条射线AB;
知1-讲
知1-讲
(2)用圆规量出已知线段的长度a(测量时使圆规两
只脚的顶点分别与线段两端点重合,则圆规
两只脚的顶点之间的距离即为线段的长度);
(3)在射线AB上用圆规截取AC使AC=a,则线段
AC即为所求的线段,如图.
2
知识点
线段大小的比较
知2-导
考考你的眼力
A
B
C
D
线段AB和线段CD哪一条长
知2-讲
生活中的长短的比较
思考 请同学们思考并回答下面的问题:
(1) 怎样比较两个同学的高矮
(2) 怎样比较两根筷子的长短
知2-讲
比较两根筷子的长短的方法:
——重合法.
① 一头对齐,两根棒靠紧, 观察另一头的位置;
注意:在几何里更多的用前面所说的方法进行比较.
② 用刻度尺分别度量出筷子的长度.
多出一段的较长.
同一长度单位下,数量大的较长.
——度量法.
知2-讲
线段长短的比较方法:
(1)度量法,用刻度尺分别量出两条线段的长度
再比较;
(2)叠合法,使两条线段的一个端点重合,另一
个端点在同一侧,从而比较出两条线段的长
短.
2
知识点
线段大小的比较
知2-导
考考你的眼力
A
B
C
D
线段AB和线段CD哪一条长
知2-讲
点D在AB的延长线上
点D与B重合
点D在AB上
AB>CD
AB=CD
ABB
A
C
D
B
C
A
A
C
B
D
D
例2 如图所示,是一张三角形纸片,你能比较线段
AB与线段BC的长短吗?
导引:可以利用度量法,分别量出每条线段的长度,
然后进行比较,或者利用叠合法进行比较.
解:把边BC折到AB上,使AB与BC重合,可知点C
在线段AB上,所以AB>BC.
知2-讲
总 结
知2-讲
比较两条线段的长短可以用叠合法或度量法,
如果使用叠合法,就设法将两线段一端端点重合,
另外两个端点放在公共端点的同侧,再观察另外两
个端点的位置关系;如果使用度量法,则分别度量
出两条线段的长,然后比较度量值的大小.
归纳总结:
线段比较的方法
叠合法
度量法
数
形
1 下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
2 比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
知2-练
A
D
例1 已知线段a,b,如图①,画线段AC=a+b.
导引:通过尺规作图把两条线段转移到同一条直
线上,连接在一起即可.
解:步骤1:画直线AD;
步骤2:在直线AD上依次截取AB=a,BC=b,
则线段AC=a+b,如图②.
知1-讲
①
②
问题三:已知线段a,b(b>a)画一条线段AC,使AC=b-a。
a
b
想一想
知1-练
2 如图,已知线段a,b,作线段AB,使AB=2a
-b(注明作图步骤).
解:如图,
(1)作射线AE;
(2)在射线AE上顺次截取AC=CD=a;
(3)在线段AD上截取DB=b,则线段AB即为
所求作的线段.
总 结
知1-讲
作线段的和及倍数问题,一般都在所作直线上
依次截取;作线段的差在被减数的线段内也依次截
取,余下的线段即为所求线段的差.
3
知识点
线段的中点
知3-讲
1.中点的概念 :
若点M把线段AB分成相等的两条线段AM和BM, 则点M叫线段AB的中点.
A
B
M
=
AM
BM
=
AB
知3-讲
2.对线段的中点的认识:
(1)线段的中点是线段上的点,且把线段分成相等
的两条线段;
(2)一条线段的中点有且只有一个;
(3)如图,若M是AB的中点,则①AM=BM= AB;
②AB=2AM=2BM;③AM+BM=AB且AM=
BM.反过来也成立.
例3 如图,M是线段AB的中点,N是线段AM上
一点,则下列结论不一定成立的是( )
A.MN=BM-AN
B.MN= AB-AN
C.MN= AM
D.MN=BN-AM
导引:由图知MN=AM-AN,由线段中点定义知
AM=BM= AB,所以A,B正确;又由图
知MN=BN-BM,易知D正确.
知3-讲
C
总 结
知3-讲
解答有关线段之间关系的题,一般要根据题中给
定的条件,结合图中已有条件进行解答,如本例我们
是根据线段中点定义得出的线段关系,结合图中MN
与其他线段关系来进行解答的.
例4 画线段MN=3 cm,在线段MN上取一点Q,
使MQ=NQ;延长线段MN到点A,使AN=
MN;延长线段NM到点B,使BM= BN.
计算:(1)线段BM的长;(2)线段AN的长.
导引:首先根据题意画出图形,再从图形中寻找数
量关系进行计算.
知3-讲
解:如图.
(1)因为MN=3 cm,MQ=NQ,
所以MQ=NQ=1.5 cm.
又因为BM= BN,
所以MN= BN,即BN= MN=4.5 cm.
所以BM=BN-MN=1.5 cm.
(2)因为AN= MN,MN=3 cm,
所以AN=1.5 cm.
知3-讲
1 下列说法正确的是( )
A.若AC= AB,则C是AB的中点
B.若AB=2CB,则C是AB的中点
C.若AC=BC,则C是AB的中点
D.若AC=BC= AB,则C是AB的中点
知3-练
D
2 如图,C是线段AB上的一点,M是线段AC的
中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
知3-练
B
这节课你学会了什么?
1. 用尺规作线段.
2.线段的两种比较方法:叠合法和度量法.
3.线段的中点的概念及表示方法.
归纳总结
本节课的主要内容如下
直线、射线、线段(二)
知识技能
线段的比较
线段的和、差
线段的中点
思想方法
数形结合
1.必做: 完成教材P128练习T1-T3,
P129习题4.2T5-T7,T9,T10
第四章 几何图形初步
4.2 直线、射线、线段
第2课时 线段的比较
1
课堂讲解
尺规作图
线段大小的比较
线段的中点
2
课时流程
逐点
导讲练
课堂小结
课后作业
A
B
图1
b
图2
a
图3
O
A
图4
A
B
图5
下面图形中,哪些是直线、射线和线段
1
知识点
尺规作图
尺规作图:在数学中,我们常限定用无刻度的直尺
和圆规作图,这就是尺规作图,利用尺规作图可以
将一条线段移到另一条线段上.用直尺(无刻度)和
圆规作一条线段等于已知线段的步骤:
(1)利用直尺(无刻度)作一条射线AB;
知1-讲
知1-讲
(2)用圆规量出已知线段的长度a(测量时使圆规两
只脚的顶点分别与线段两端点重合,则圆规
两只脚的顶点之间的距离即为线段的长度);
(3)在射线AB上用圆规截取AC使AC=a,则线段
AC即为所求的线段,如图.
2
知识点
线段大小的比较
知2-导
考考你的眼力
A
B
C
D
线段AB和线段CD哪一条长
知2-讲
生活中的长短的比较
思考 请同学们思考并回答下面的问题:
(1) 怎样比较两个同学的高矮
(2) 怎样比较两根筷子的长短
知2-讲
比较两根筷子的长短的方法:
——重合法.
① 一头对齐,两根棒靠紧, 观察另一头的位置;
注意:在几何里更多的用前面所说的方法进行比较.
② 用刻度尺分别度量出筷子的长度.
多出一段的较长.
同一长度单位下,数量大的较长.
——度量法.
知2-讲
线段长短的比较方法:
(1)度量法,用刻度尺分别量出两条线段的长度
再比较;
(2)叠合法,使两条线段的一个端点重合,另一
个端点在同一侧,从而比较出两条线段的长
短.
2
知识点
线段大小的比较
知2-导
考考你的眼力
A
B
C
D
线段AB和线段CD哪一条长
知2-讲
点D在AB的延长线上
点D与B重合
点D在AB上
AB>CD
AB=CD
AB
A
C
D
B
C
A
A
C
B
D
D
例2 如图所示,是一张三角形纸片,你能比较线段
AB与线段BC的长短吗?
导引:可以利用度量法,分别量出每条线段的长度,
然后进行比较,或者利用叠合法进行比较.
解:把边BC折到AB上,使AB与BC重合,可知点C
在线段AB上,所以AB>BC.
知2-讲
总 结
知2-讲
比较两条线段的长短可以用叠合法或度量法,
如果使用叠合法,就设法将两线段一端端点重合,
另外两个端点放在公共端点的同侧,再观察另外两
个端点的位置关系;如果使用度量法,则分别度量
出两条线段的长,然后比较度量值的大小.
归纳总结:
线段比较的方法
叠合法
度量法
数
形
1 下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
2 比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
知2-练
A
D
例1 已知线段a,b,如图①,画线段AC=a+b.
导引:通过尺规作图把两条线段转移到同一条直
线上,连接在一起即可.
解:步骤1:画直线AD;
步骤2:在直线AD上依次截取AB=a,BC=b,
则线段AC=a+b,如图②.
知1-讲
①
②
问题三:已知线段a,b(b>a)画一条线段AC,使AC=b-a。
a
b
想一想
知1-练
2 如图,已知线段a,b,作线段AB,使AB=2a
-b(注明作图步骤).
解:如图,
(1)作射线AE;
(2)在射线AE上顺次截取AC=CD=a;
(3)在线段AD上截取DB=b,则线段AB即为
所求作的线段.
总 结
知1-讲
作线段的和及倍数问题,一般都在所作直线上
依次截取;作线段的差在被减数的线段内也依次截
取,余下的线段即为所求线段的差.
3
知识点
线段的中点
知3-讲
1.中点的概念 :
若点M把线段AB分成相等的两条线段AM和BM, 则点M叫线段AB的中点.
A
B
M
=
AM
BM
=
AB
知3-讲
2.对线段的中点的认识:
(1)线段的中点是线段上的点,且把线段分成相等
的两条线段;
(2)一条线段的中点有且只有一个;
(3)如图,若M是AB的中点,则①AM=BM= AB;
②AB=2AM=2BM;③AM+BM=AB且AM=
BM.反过来也成立.
例3 如图,M是线段AB的中点,N是线段AM上
一点,则下列结论不一定成立的是( )
A.MN=BM-AN
B.MN= AB-AN
C.MN= AM
D.MN=BN-AM
导引:由图知MN=AM-AN,由线段中点定义知
AM=BM= AB,所以A,B正确;又由图
知MN=BN-BM,易知D正确.
知3-讲
C
总 结
知3-讲
解答有关线段之间关系的题,一般要根据题中给
定的条件,结合图中已有条件进行解答,如本例我们
是根据线段中点定义得出的线段关系,结合图中MN
与其他线段关系来进行解答的.
例4 画线段MN=3 cm,在线段MN上取一点Q,
使MQ=NQ;延长线段MN到点A,使AN=
MN;延长线段NM到点B,使BM= BN.
计算:(1)线段BM的长;(2)线段AN的长.
导引:首先根据题意画出图形,再从图形中寻找数
量关系进行计算.
知3-讲
解:如图.
(1)因为MN=3 cm,MQ=NQ,
所以MQ=NQ=1.5 cm.
又因为BM= BN,
所以MN= BN,即BN= MN=4.5 cm.
所以BM=BN-MN=1.5 cm.
(2)因为AN= MN,MN=3 cm,
所以AN=1.5 cm.
知3-讲
1 下列说法正确的是( )
A.若AC= AB,则C是AB的中点
B.若AB=2CB,则C是AB的中点
C.若AC=BC,则C是AB的中点
D.若AC=BC= AB,则C是AB的中点
知3-练
D
2 如图,C是线段AB上的一点,M是线段AC的
中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
知3-练
B
这节课你学会了什么?
1. 用尺规作线段.
2.线段的两种比较方法:叠合法和度量法.
3.线段的中点的概念及表示方法.
归纳总结
本节课的主要内容如下
直线、射线、线段(二)
知识技能
线段的比较
线段的和、差
线段的中点
思想方法
数形结合
1.必做: 完成教材P128练习T1-T3,
P129习题4.2T5-T7,T9,T10
