人教版数学九年级上册 第25章概率初步 本章复习与测试课件
文档属性
| 名称 | 人教版数学九年级上册 第25章概率初步 本章复习与测试课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 13:13:34 | ||
图片预览







文档简介
(共28张PPT)
1
人教版九年级数学上册
第二十五章 概率初步
复习课
知识点复习
1.能在现实情境中区分随机事件、不可能事件和必然事件,知道必然事件的概率为1,不可能事件的概率为0,随机事件的概率在0和1之间.
2.会灵活选用直接列举法、列表法和画树状图法求随机事件的概率.
3.会用频率估计概率解决生活中的实际问题.
2
复习目标
3
重点:用列表法、画树状图法求概率,用频率估计概率.
难点:熟练利用列表法和画树状图法求概率.
重点难点
4
情景引入
成语中的事件
中国文化博大精深,而成语更是其中的一份魂宝在数学中,我们知道有必然事件、不可能事件、随机事件等,而有些成语,恰恰能很好地解释这些数学中的概念.例如:
必然事件:瓮中捉鳖、春暖花开、落叶归根、流水不腐、生老病死、瓜熟蒂落、水到渠成.
不可能事件:长生不老、刻舟求剑、饮鸩止渴、掩耳盗铃、缘木求鱼、竹篮打水、偷天换日.
随机事件:日行千里、张冠李戴、一箭双雕、飞来横祸、惊弓之鸟、一石二鸟、开门见山.
你还能举出一些类似的例子吗
5
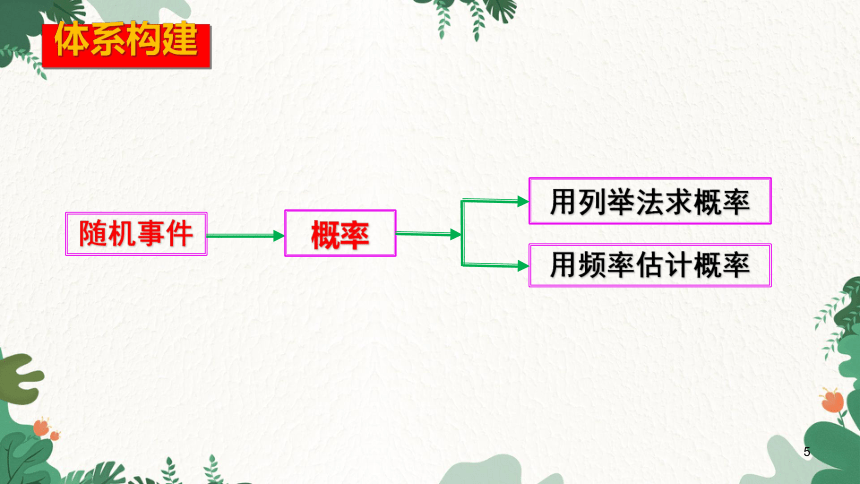
体系构建
随机事件
概率
用频率估计概率
用列举法求概率
6
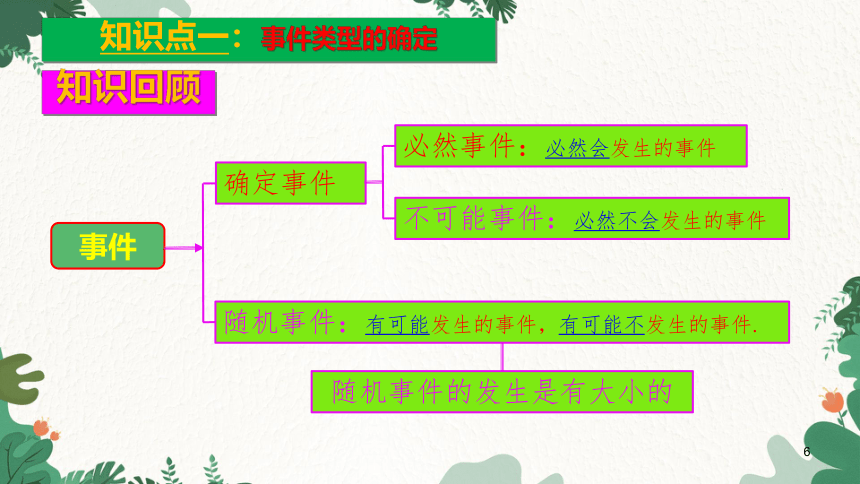
知识回顾
知识点一:事件类型的确定
事件
确定事件
随机事件:有可能发生的事件,有可能不发生的事件.
必然事件:必然会发生的事件
不可能事件:必然不会发生的事件
随机事件的发生是有大小的
7
巩固练习
知识点一:事件类型的确定
1.下列说法正确的是( )
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随机事件
D.“经过有交通信号灯的路口,遇到红灯”是必然事件
2.(易错题)不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A.摸出的是3个白球 B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球 D.摸出的是2个黑球、1个白球
C
A
8
巩固练习
知识点一:事件类型的确定
3.小明同学买了2元一注的爱心福利彩票5注,则“小明中奖”的事件为 事件.(填“必然”或“不可能”或“随机”)
4.判断下列事件哪些是随机事件,哪些是必然事件,哪些是不可能事件.
(1)366人中至少有两人生日是同一天(一年按365天计算).
(2)随意翻一下日历,翻到的号数是偶数.
(3)两条直线被第三条直线所截,同位角相等.
(4)从一副扑克牌中随意抽出一张,抽到黑桃A
(5)当x<0时,x2<0.
随机事件
随机事件
随机事件
必然事件
不可能事件
随机
9
巩固练习
知识点一:事件类型的确定
5.下列成语故事反映的事件哪些是随机事件,哪些是必然事件,哪些是不可能事件.
(1)拔苗助长
(2)守株待兔
(3)海底捞月
(4)瓮中捉鳖
(5)一箭双雕
(6)刻舟求剑
不可能事件
随机事件
必然事件
不可能事件
不可能事件
随机事件
10
知识回顾
知识点二:随机事件发生的可能性
概率
随机事件A发生的概率,记为 .
不可能事件发生的概率,P(A)=0
事件A发生的概率P(A)= ,且0≤ P(A) ≤1.
必然事件发生的概率,P(A)=1;.
11
知识点二:随机事件发生的可能性
1. 掷一枚质地均匀的硬币10次,下列说法正确的是( )
A.每2次必有1次正面向上 B.必有5次正面向上
C.可能有7次正面向上 D.不可能有10次正面向上
2. 对“阜阳市明天下雨的概率是75%”这句话,理解正确的是( )
A.阜阳市明天将有75%的时间下雨
B.阜阳市明天将有75%的地区下雨
C.阜阳市明天一定下雨
D.阜阳市明天下雨的可能性较大
C
D
巩固练习
概率的意义
12
巩固练习
知识点二:随机事件发生的可能性
3.下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机摸出一个球,一定是红球;
B.天气预报“明天下雨的概率为70%”,指明天有70%的时间会下雨;
C.某地发行一种福利彩票,中一等奖的概率是0.001,那么买这种彩票1000张,一定会中一等奖;
D.抛掷一枚质地均匀的正六面体骰子,朝上的面的数字是奇数和偶数的概率相同.
D
概率的意义
13
知识回顾
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率
P(A)=
在P(A)= 中,由m和n的含义,可知0≤m≤n,进而有
0≤ ≤1. 因此 0≤ P(A) ≤1.
知识点二:随机事件发生的可能性
14
特别地, 当A为必然事件时,P(A)=1;
当A为不可能事件时,P(A)=0.
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能发生
必然发生
概率的值
知识回顾
知识点二:随机事件发生的可能性
15
巩固练习
知识点二:随机事件发生的可能性
概率的简单计算
1.有五张背面完全相同的卡片,正面分别写有 ,( ),
, ,2-2,把卡片背面朝上洗匀后,从中随1机抽取一张,其正面的数字是无理数的概率是( )
A. B. C. D.
2.任取不等式组 的一个整数解,则能使关于x的方程2x+k=-1的解为非负数的概率为 .
A
k-3≤0
2k+5>0
16
巩固练习
知识点二:随机事件发生的可能性
概率的简单计算
3.从-2,-1,0,1,2这5个数中任取一个数,作为关于x的一元二次方程x2-x+k=0的k值,则所得的方程中有两个不相等的实数根的概率是 .
4.如图,A,B是由边长为1的小正方形
组成的网格上的两个格点,在格点中任
意放置点C,恰好能使A,B,C三点构
成三角形且面积为1的概率是 .
17
知识回顾
知识点三:列举法求随机事件的概率
用列举法求概率
直接列举法
列表法
求简单等可能事件的概率的步骤:
(1)确定 ;
(2)找出 ;
(3)用 进行求解.
所有等可能的结果n
相应事件A出现的所有结果m
P(A)=
18
巩固练习
知识点三:列举法求随机事件的概率
1.从-3,-1,0,2四个数中任选两个,则这两个数的乘积为负数的概率为( )
A. B. C. D.
2.一个不透明的布袋中装有分别标着数字1,2,3,4的四个相同的乒乓球,现从袋中随机摸出两个乒兵球,则这两个乒兵球上的数字之和大
于5的概率为( )
A. B. C. D.
B
B
19
巩固练习
知识点三:列举法求随机事件的概率
3.在一个不透明的袋子里装有一个黑球和一个白球,它们除颜色外其余都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后再随机摸出一个球,两次都摸到黑球的概率是( )
A. B. C. D.
A
20
巩固练习
知识点三:列举法求随机事件的概率
4.从数-2,- ,0,4中任取一个数记为m,再从余下的三个数中,任取个数记为n,若k=mn,求正比例函数y=kx的图象经过第一、三象限的概率.
解:列举所有结果为(-2, ),(-2,0),(-2,4),( ,0),( ,4),(0,4),其中k=mn>0的结果数为1种,
∴正比例函数y=kx的图象经过第一、三象限的概率是
21
知识回顾
知识点三:列举法求随机事件的概率
画树状图求概率的步骤
1.画树状图.
3.利用公式求概率.
2.列出结果,确定公式P(A)= 中的m和n的值.
22
巩固练习
知识点三:列举法求随机事件的概率
1.小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗 请说明理由.
23
巩固练习
知识点三:列举法求随机事件的概率
2.(安徽中考改编)如图,管中放置着三根同样绳子AA1、BB1、CC1.小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求绳子能连结成一个封闭圆的概率.
24
归纳总结
知识点三:列举法求随机事件的概率
用列表或画树状图的方法求事件概率.值得注意的是:在列表或画树状图时,要注意是“放回”还是“不放回”问题,不放回时列表要去掉对角线.通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件的结果数目m,然后利用概率公式求事件的概率.
25
知识回顾
知识点四:用频率估计概率
用频率估计概率
一般地,在大量重复试验中,如果事件A发生的频率 稳定于某个常数 p,那么事件A发生的概率:P(A)= p
26
巩固练习
知识点四:用频率估计概率
1.为了估计水塘中的鱼的数量,养鱼者首先从鱼塘中捕获30条鱼,在每条鱼身上做好标记,把这些鱼放回鱼塘,过一段时间,估计这些鱼与鱼塘中的鱼完全混合后,再从鱼塘中捕捞200条鱼,发现其中带有记号的鱼有5条,由此他估计鱼塘中共有鱼( )A.3000条 B.2200条 C.1200条 D.600条
2.在一个不透明的口袋中,装有红色、黑色、白色的玻璃球共40个,除颜色外其余都相同,小明通过许多次摸球试验后发现,其中摸到红色球黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( ) A.18 B.17 C.16 D.15
C
C
27
巩固练习
知识点四:用频率估计概率
3.做重复试验:抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则可以估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
A.0.22 B.0.44 C.0.50 D.0.56
D
28
知识网图
事件的识别
随机事件
不可能事件发生的概率,P(A)=0
必然事件发生的概率,P(A)=1;.
概率P(A)= ,且0≤ P(A) ≤1.
概率的求法
列举法求概率
用频率估计概率
直接列举法
列表法
画树状图
1
人教版九年级数学上册
第二十五章 概率初步
复习课
知识点复习
1.能在现实情境中区分随机事件、不可能事件和必然事件,知道必然事件的概率为1,不可能事件的概率为0,随机事件的概率在0和1之间.
2.会灵活选用直接列举法、列表法和画树状图法求随机事件的概率.
3.会用频率估计概率解决生活中的实际问题.
2
复习目标
3
重点:用列表法、画树状图法求概率,用频率估计概率.
难点:熟练利用列表法和画树状图法求概率.
重点难点
4
情景引入
成语中的事件
中国文化博大精深,而成语更是其中的一份魂宝在数学中,我们知道有必然事件、不可能事件、随机事件等,而有些成语,恰恰能很好地解释这些数学中的概念.例如:
必然事件:瓮中捉鳖、春暖花开、落叶归根、流水不腐、生老病死、瓜熟蒂落、水到渠成.
不可能事件:长生不老、刻舟求剑、饮鸩止渴、掩耳盗铃、缘木求鱼、竹篮打水、偷天换日.
随机事件:日行千里、张冠李戴、一箭双雕、飞来横祸、惊弓之鸟、一石二鸟、开门见山.
你还能举出一些类似的例子吗
5
体系构建
随机事件
概率
用频率估计概率
用列举法求概率
6
知识回顾
知识点一:事件类型的确定
事件
确定事件
随机事件:有可能发生的事件,有可能不发生的事件.
必然事件:必然会发生的事件
不可能事件:必然不会发生的事件
随机事件的发生是有大小的
7
巩固练习
知识点一:事件类型的确定
1.下列说法正确的是( )
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随机事件
D.“经过有交通信号灯的路口,遇到红灯”是必然事件
2.(易错题)不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A.摸出的是3个白球 B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球 D.摸出的是2个黑球、1个白球
C
A
8
巩固练习
知识点一:事件类型的确定
3.小明同学买了2元一注的爱心福利彩票5注,则“小明中奖”的事件为 事件.(填“必然”或“不可能”或“随机”)
4.判断下列事件哪些是随机事件,哪些是必然事件,哪些是不可能事件.
(1)366人中至少有两人生日是同一天(一年按365天计算).
(2)随意翻一下日历,翻到的号数是偶数.
(3)两条直线被第三条直线所截,同位角相等.
(4)从一副扑克牌中随意抽出一张,抽到黑桃A
(5)当x<0时,x2<0.
随机事件
随机事件
随机事件
必然事件
不可能事件
随机
9
巩固练习
知识点一:事件类型的确定
5.下列成语故事反映的事件哪些是随机事件,哪些是必然事件,哪些是不可能事件.
(1)拔苗助长
(2)守株待兔
(3)海底捞月
(4)瓮中捉鳖
(5)一箭双雕
(6)刻舟求剑
不可能事件
随机事件
必然事件
不可能事件
不可能事件
随机事件
10
知识回顾
知识点二:随机事件发生的可能性
概率
随机事件A发生的概率,记为 .
不可能事件发生的概率,P(A)=0
事件A发生的概率P(A)= ,且0≤ P(A) ≤1.
必然事件发生的概率,P(A)=1;.
11
知识点二:随机事件发生的可能性
1. 掷一枚质地均匀的硬币10次,下列说法正确的是( )
A.每2次必有1次正面向上 B.必有5次正面向上
C.可能有7次正面向上 D.不可能有10次正面向上
2. 对“阜阳市明天下雨的概率是75%”这句话,理解正确的是( )
A.阜阳市明天将有75%的时间下雨
B.阜阳市明天将有75%的地区下雨
C.阜阳市明天一定下雨
D.阜阳市明天下雨的可能性较大
C
D
巩固练习
概率的意义
12
巩固练习
知识点二:随机事件发生的可能性
3.下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机摸出一个球,一定是红球;
B.天气预报“明天下雨的概率为70%”,指明天有70%的时间会下雨;
C.某地发行一种福利彩票,中一等奖的概率是0.001,那么买这种彩票1000张,一定会中一等奖;
D.抛掷一枚质地均匀的正六面体骰子,朝上的面的数字是奇数和偶数的概率相同.
D
概率的意义
13
知识回顾
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率
P(A)=
在P(A)= 中,由m和n的含义,可知0≤m≤n,进而有
0≤ ≤1. 因此 0≤ P(A) ≤1.
知识点二:随机事件发生的可能性
14
特别地, 当A为必然事件时,P(A)=1;
当A为不可能事件时,P(A)=0.
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能发生
必然发生
概率的值
知识回顾
知识点二:随机事件发生的可能性
15
巩固练习
知识点二:随机事件发生的可能性
概率的简单计算
1.有五张背面完全相同的卡片,正面分别写有 ,( ),
, ,2-2,把卡片背面朝上洗匀后,从中随1机抽取一张,其正面的数字是无理数的概率是( )
A. B. C. D.
2.任取不等式组 的一个整数解,则能使关于x的方程2x+k=-1的解为非负数的概率为 .
A
k-3≤0
2k+5>0
16
巩固练习
知识点二:随机事件发生的可能性
概率的简单计算
3.从-2,-1,0,1,2这5个数中任取一个数,作为关于x的一元二次方程x2-x+k=0的k值,则所得的方程中有两个不相等的实数根的概率是 .
4.如图,A,B是由边长为1的小正方形
组成的网格上的两个格点,在格点中任
意放置点C,恰好能使A,B,C三点构
成三角形且面积为1的概率是 .
17
知识回顾
知识点三:列举法求随机事件的概率
用列举法求概率
直接列举法
列表法
求简单等可能事件的概率的步骤:
(1)确定 ;
(2)找出 ;
(3)用 进行求解.
所有等可能的结果n
相应事件A出现的所有结果m
P(A)=
18
巩固练习
知识点三:列举法求随机事件的概率
1.从-3,-1,0,2四个数中任选两个,则这两个数的乘积为负数的概率为( )
A. B. C. D.
2.一个不透明的布袋中装有分别标着数字1,2,3,4的四个相同的乒乓球,现从袋中随机摸出两个乒兵球,则这两个乒兵球上的数字之和大
于5的概率为( )
A. B. C. D.
B
B
19
巩固练习
知识点三:列举法求随机事件的概率
3.在一个不透明的袋子里装有一个黑球和一个白球,它们除颜色外其余都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后再随机摸出一个球,两次都摸到黑球的概率是( )
A. B. C. D.
A
20
巩固练习
知识点三:列举法求随机事件的概率
4.从数-2,- ,0,4中任取一个数记为m,再从余下的三个数中,任取个数记为n,若k=mn,求正比例函数y=kx的图象经过第一、三象限的概率.
解:列举所有结果为(-2, ),(-2,0),(-2,4),( ,0),( ,4),(0,4),其中k=mn>0的结果数为1种,
∴正比例函数y=kx的图象经过第一、三象限的概率是
21
知识回顾
知识点三:列举法求随机事件的概率
画树状图求概率的步骤
1.画树状图.
3.利用公式求概率.
2.列出结果,确定公式P(A)= 中的m和n的值.
22
巩固练习
知识点三:列举法求随机事件的概率
1.小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗 请说明理由.
23
巩固练习
知识点三:列举法求随机事件的概率
2.(安徽中考改编)如图,管中放置着三根同样绳子AA1、BB1、CC1.小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求绳子能连结成一个封闭圆的概率.
24
归纳总结
知识点三:列举法求随机事件的概率
用列表或画树状图的方法求事件概率.值得注意的是:在列表或画树状图时,要注意是“放回”还是“不放回”问题,不放回时列表要去掉对角线.通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件的结果数目m,然后利用概率公式求事件的概率.
25
知识回顾
知识点四:用频率估计概率
用频率估计概率
一般地,在大量重复试验中,如果事件A发生的频率 稳定于某个常数 p,那么事件A发生的概率:P(A)= p
26
巩固练习
知识点四:用频率估计概率
1.为了估计水塘中的鱼的数量,养鱼者首先从鱼塘中捕获30条鱼,在每条鱼身上做好标记,把这些鱼放回鱼塘,过一段时间,估计这些鱼与鱼塘中的鱼完全混合后,再从鱼塘中捕捞200条鱼,发现其中带有记号的鱼有5条,由此他估计鱼塘中共有鱼( )A.3000条 B.2200条 C.1200条 D.600条
2.在一个不透明的口袋中,装有红色、黑色、白色的玻璃球共40个,除颜色外其余都相同,小明通过许多次摸球试验后发现,其中摸到红色球黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( ) A.18 B.17 C.16 D.15
C
C
27
巩固练习
知识点四:用频率估计概率
3.做重复试验:抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则可以估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
A.0.22 B.0.44 C.0.50 D.0.56
D
28
知识网图
事件的识别
随机事件
不可能事件发生的概率,P(A)=0
必然事件发生的概率,P(A)=1;.
概率P(A)= ,且0≤ P(A) ≤1.
概率的求法
列举法求概率
用频率估计概率
直接列举法
列表法
画树状图
同课章节目录
