人教版数学九年级上册 第23章 旋转 本章复习与测试课件(共37张PPT)
文档属性
| 名称 | 人教版数学九年级上册 第23章 旋转 本章复习与测试课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 13:15:04 | ||
图片预览







文档简介
(共37张PPT)
1
人教版九年级数学上册
第二十三章 旋转
复 习 课
知识点复习
1.知道旋转的概念及性质,能应用旋转的性质进行简单的证明,会作一个图形旋转后的图形.
2.知道中心对称、中心对称图形的概念及性质,会判断一个图形是不是中心对称图形.能熟练说出一个点关于原点对称的点的坐标.
3.能灵活应用平移、旋转、轴对称变换进行图案设计,体会数学的美感.
2
复习目标
重点:旋转的性质、作图,中心对称、中心对称图形及其性质.
难点:中心对称、中心对称图形的关系及其性质.
3
重点难点
4
知识结构图
5
知识点一:旋转及其性质
知识回顾
在描述一个旋转过程时,需要指明旋转的三要素,即转中心、旋转方向和旋转角,三者缺一不可.
分析旋转形成的方法可简记为三个“ー",即一个定点,一个方向,一个角度.
6
知识回顾
知识点一:旋转及其性质
旋转的性质:
①对应点到旋转中心的距离相等
②对应点与旋转中心所连线段的夹角等于旋转角
③旋转前、后的图形全等
几何语言
A′
B′
C′
O
A
B
C
∵△A′B′C′是由△ABC旋转得到的,
∴OA= OA′、OB=OB′、OC=OC′
∠AOA′=∠BOB′=∠COC′, ABC≌ A′B′C′
7
巩固练习
知识点一:旋转及其性质
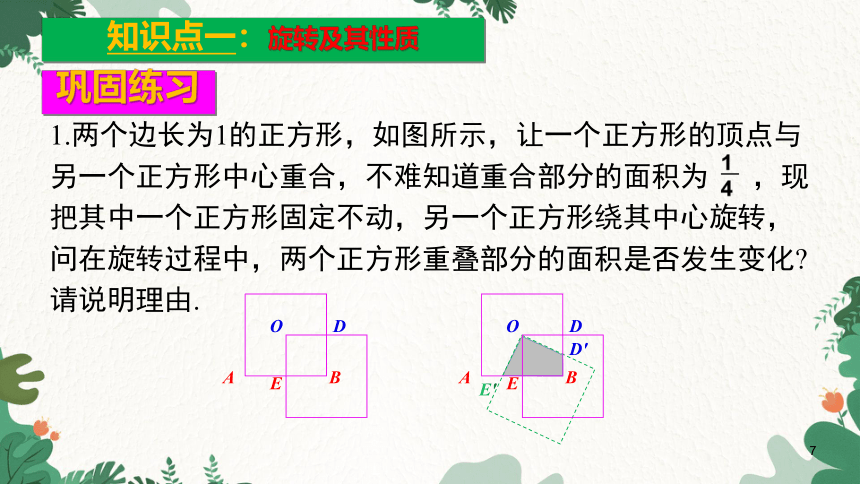
1.两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为 ,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分的面积是否发生变化 请说明理由.
A
B
D
O
E
E′
D′
A
B
D
O
E
8
巩固练习
知识点一:旋转及其性质
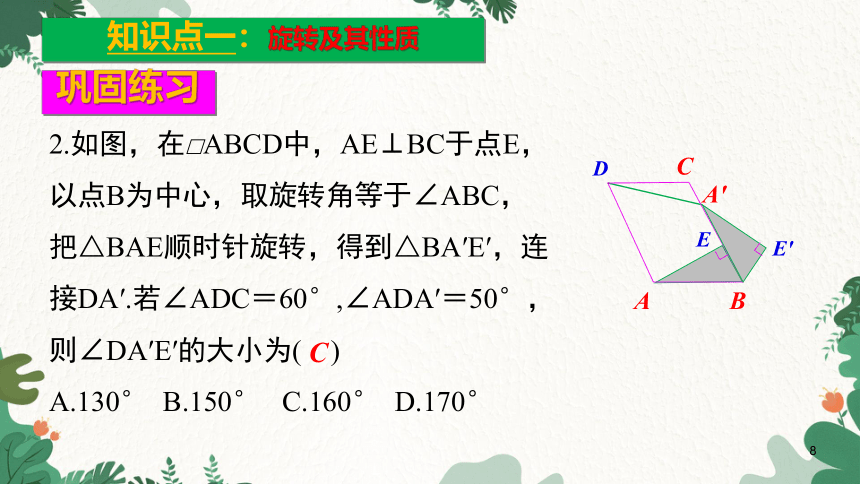
2.如图,在□ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
A.130° B.150° C.160° D.170°
A
B
D
E
C
E′
A′
∟
∟
C
9
巩固练习
知识点一:旋转及其性质
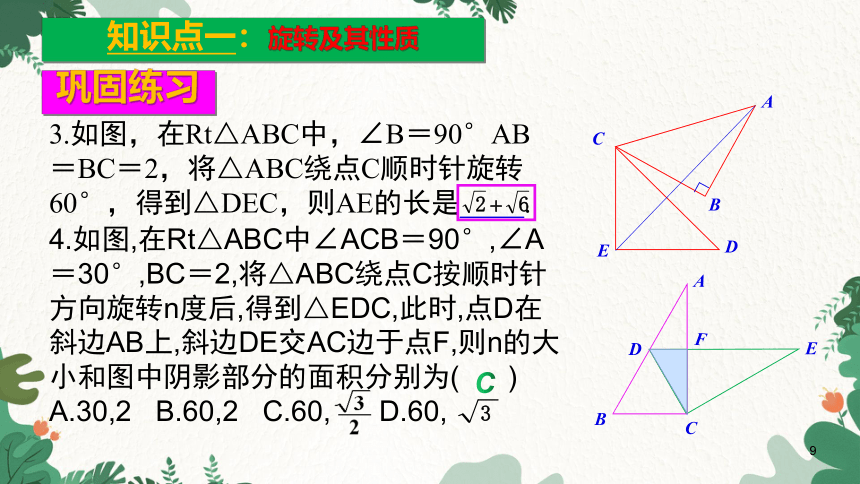
3.如图,在Rt△ABC中,∠B=90°AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .
4.如图,在Rt△ABC中∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在斜边AB上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A.30,2 B.60,2 C.60, D.60,
A
B
C
D
E
F
C
A
B
C
D
E
∟
10
巩固练习
知识点一:旋转及其性质
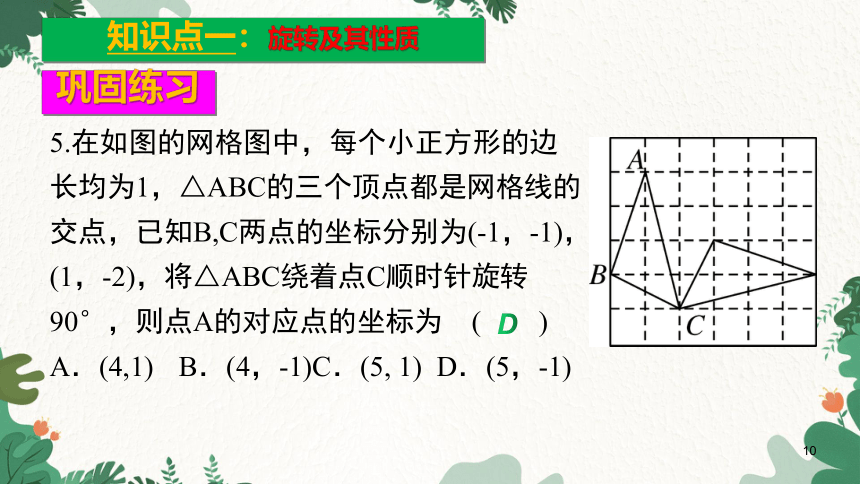
5.在如图的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为 ( )
A.(4,1) B.(4,-1)C.(5, 1) D.(5,-1)
D
11
巩固练习
知识点一:旋转及其性质
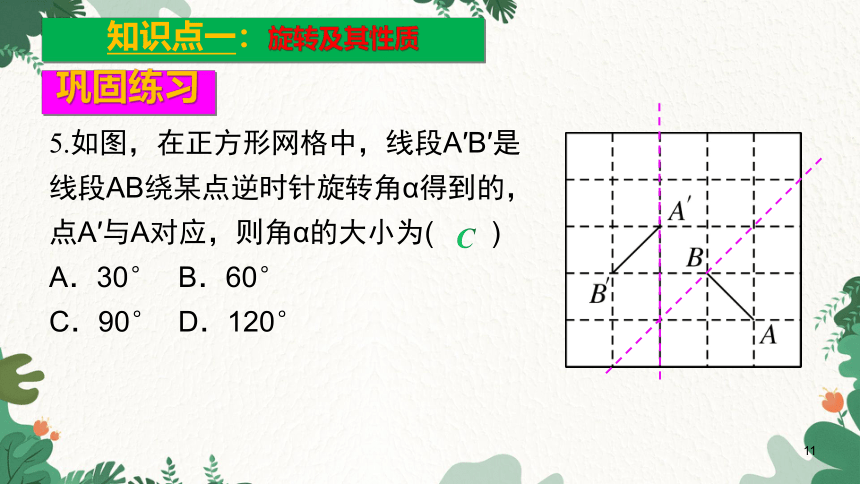
5.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
A.30° B.60°
C.90° D.120°
C
12
知识回顾
知识点二:中心对称及中心对称图形
“中心对称与轴对称的对比”
中心对称 轴对称
不同点
相同点
图形绕对称中心旋转180° 图形沿对称轴折叠
图形旋转后与另一个图形重合 图形折叠后与另一个图形重合
对称中心只有一个 至少有一条对称轴
都是两个图形之间的关系,而且变换前、后两个图形全等
13
知识回顾
知识点二:中心对称及中心对称图形
O
A
B
C
A′
B′
C′
1.中心对称的两个图形,对称点所连线段都经过 ,而且被 所平分。
2.关于中心对称的两个图形是 。
中心对称的性质:
对称中心
对称中心
全等形
几何语言
∵ ABC和 A′B′C′关于点O成中心对称
∴OA=OA′,OB=OB′,OC=OC′
ABC≌ A′B′C′
14
知识回顾
知识点二:中心对称及中心对称图形
中心对称图形 轴对称图形
区别
举例
中心对称图形与轴对称图形的对比
(1)是关于某一点对称 (1)是某一条直线对称
(2)是绕某一点旋转180°后与原来的图象重合
线段、平行四边形、矩形、菱形、边数是偶数的正多边形、圆等都是中心对称图形
线段、角、等腰三角形、矩形、菱形、正多边形等都是轴对称图形
(2)是沿一条直线折叠后,直线两旁的部分互相重合
15
知识回顾
知识点二:中心对称及中心对称图形
中心对称 中心对称图形
区别
联系
中心对称与中心对称图形的区别和联系
(1)是针对两个图形而言的 (1)是针对一个图形而言的
(2)是指两个图形的(位置)关系 (2)是指具有某种性质的一个图形
(3)对称点在两个图形上 (3)对称点在一个图形上
(4)对称中心可能在两个图形的外部,(4)对称中心在图形内部.
也可能在图形的内部或图形上.
(1)都是根据把图形旋转180°后能重合定义的.
(2)两者可以相互转化,若把成中心对称的两个图形视为一个整体,则整个图形是中心对称图形;若把一个中心对称图形相互对称的两部分看作两个图形,则这两个图形成中心对称
16
知识回顾
知识点二:中心对称及中心对称图形
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分.即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等)
中心对称图形的性质
17
巩固练习
知识点二:中心对称及中心对称图形
1.下列说法中,①线段两端点关于它的中点对称;
②菱形一组对边关于对角线交点对称;
③成中心对称的两个图形一定全等;
④如果两个图形全等,那么这两个图形一定关于某点成中心对称;
⑤如果两个三角形的对应点连线都经过一点,那么这两个三角形成中心对称.其中正确的有 (填序号).
①②③
18
巩固练习
知识点二:中心对称及中心对称图形
2.如图,在Rt△ABC中,斜边AB长为 ,直角边BC长为12,若扇形ACE与扇形BDE关于点E成中心对称,则图中阴影部分的面积为 .
19
巩固练习
知识点二:中心对称及中心对称图形
B
3.下列所述图形中,是中心对称图形的是( )
A直角三角形 B.平行四边形 C.正五边形 D.正三角形
4.下列图形:①圆;②正五边形;③正方形:④抛物线y=x2其中既是中心对称图形又是轴对称图形的是 (填序号)
5.右图中,中心对
称图形有( )
A.4个B.3个C.2个,D.1个
①③
B
20
巩固练习
知识点二:中心对称及中心对称图形
6.如图,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD,BC分别交于点E,F,则图中相等的线段有( )
A.3对 B.4对 C.5对 D.6对
7.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为 .
A
B
D
C
O
E
F
21
巩固练习
知识点二:中心对称及中心对称图形
8.如图所示的放置着两个矩形,请你作一条直线,将此图形分成面积相等的两部分.(不写作法,保留作图痕迹)
22
知识回顾
知识点三:关于原点对称的点的坐标
两个点关于原点对称时,
它们的坐标符号相反,
即点P(x,y)关于原点的对称点为P′(﹣x,﹣y).
A
B
C
D
E
A′
B′
C′
D′
E′
(2,1)
(-2,-1)
23
知识回顾
知识点三:关于原点对称的点的坐标
名 称 区 别 举 例
关于坐标轴对称 关于x轴对称
关于y轴对称
关于原点对称
横坐标相等,
纵坐标互为相反数.
点P(x,y)关于x轴对称的点P1为(x,-y).
纵坐标相等,
横坐标互为相反数.
点P(x,y)关于y轴对称的点P2为(-x,y).
纵,横坐标分别互为相反数.
点P(x,y)关于原点对称的点P3为(-x,-y).
24
知识回顾
知识点三:关于原点对称的点的坐标
两个点关于直线y=x对称时,
它们的坐标互换,
即点P(x,y)关于直线y=x的对称点为P1(y,x).
A
B
C
D
E
A′
B′
C′
D′
E′
(2,1)
(1,2)
25
知识回顾
知识点三:关于原点对称的点的坐标
两个点关于直线y= - x对称时,
它们的纵横坐标互换且符号改变,
即点P(x,y)关于直线y= - x的对称点为P2(-y,-x).
A
B
C
D
E
A′′
B′′
C′′
D′′
E′′
(2,1)
(-1,-2)
26
知识回顾
知识点三:关于原点对称的点的坐标
①P(x,y)
设点P的坐标为(x,y),那么有下列结论:
关于x轴对称
P(x,-y)
②P(x,y)
关于y轴对称
P(-x,y)
③P(x,y)
关于y=x对称
P(y,x)
④P(x,y)
关于y=-x对称
P(-y,-x)
⑤P(x,y)
关于原点对称
P(-x,-y)
27
巩固练习
知识点三:关于原点对称的点的坐标
1.点P(-2,3)关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.将点A(3,2)沿y轴正方向平移3个单位长度得到点B,则点B关于原点的对称点的坐标为( )
A.(3,5) B.(5,3) C.(-3,-5) D.(-5,-3)
3.已知点A(a,-3)与点A′(5,b)关于坐标原点对称,则实数a,b的值是( )
A.a=5.b=3 B.a=-5.b=-3 C.a=5,b=-3 D.a=-5.b=3
D
C
D
28
巩固练习
知识点三:关于原点对称的点的坐标
4.点P(-2,3)关于直线y=x对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.将点A(3,2)沿y轴正方向平移3个单位长度得到点B,则点B关于直线y=-x的对称点的坐标为( )
A.(3,5) B.(5,3) C.(-3,-5) D.(-5,-3)
6.已知点A(a,-3)与点A′(b,5)关于直线y=-x对称,则实数a,b的值是( )
A.a=5.b=3 B.a=-5.b=-3 C.a=5,b=-3 D.a=-5.b=3
D
D
D
29
巩固练习
知识点三:关于原点对称的点的坐标
7.已知点P(a+1,- +1)关于原点的对称点在第四象限,则a的取值范围是 .
8.(易错题)已知△ABC的三边长分别为a,b,c,且满足点A(∣2c-16∣,(a- )2)与点B( ,-32)关于原点对称,则△ABC的形状是 .
9.已知点P(1-2a,a-2)关于原点的对称点在第一象限内,且a为整数,则关于x的分式方程 =-1的解是 .
x<-1
等腰直角三角形
30
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心;
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
确定对称中心的方法
知识回顾
知识点四:平移、旋转、轴对称作图
31
作已知图形关于某一点对称的图形,其作图步骤简记为:连接、延长、截取相等线段、连点成图.
在平面直角坐标系中作已知图形关于某一点对称的图形有没有其他方法?
知识回顾
知识点四:平移、旋转、轴对称作图
32
知识回顾
知识点四:平移、旋转、轴对称作图
图案设计:图案设计的变换组合一般有以下几种
(1)先平移后旋转;
(2)先旋转后平移;
(3)先转后作轴对称
(4)先作轴对称后平移
33
巩固练习
知识点二:中心对称及中心对称图形
1、如图,在平面直角坐标系中,△ABC各顶点的坐标分别为
A(-2,-2),B(-4,-1),C(-4,-4).作出△ABC关于原点0对称的△A1B1C1并写出点A1,B1,C1的坐标.
O
A
B
C
y
x
A1
B1
C1
34
巩固练习
知识点四:平移、旋转、轴对称作图
2.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
35
巩固练习
知识点四:平移、旋转、轴对称作图
3.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.1种 B.2种 C.3种 D.4种
36
思维导图
37
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1
人教版九年级数学上册
第二十三章 旋转
复 习 课
知识点复习
1.知道旋转的概念及性质,能应用旋转的性质进行简单的证明,会作一个图形旋转后的图形.
2.知道中心对称、中心对称图形的概念及性质,会判断一个图形是不是中心对称图形.能熟练说出一个点关于原点对称的点的坐标.
3.能灵活应用平移、旋转、轴对称变换进行图案设计,体会数学的美感.
2
复习目标
重点:旋转的性质、作图,中心对称、中心对称图形及其性质.
难点:中心对称、中心对称图形的关系及其性质.
3
重点难点
4
知识结构图
5
知识点一:旋转及其性质
知识回顾
在描述一个旋转过程时,需要指明旋转的三要素,即转中心、旋转方向和旋转角,三者缺一不可.
分析旋转形成的方法可简记为三个“ー",即一个定点,一个方向,一个角度.
6
知识回顾
知识点一:旋转及其性质
旋转的性质:
①对应点到旋转中心的距离相等
②对应点与旋转中心所连线段的夹角等于旋转角
③旋转前、后的图形全等
几何语言
A′
B′
C′
O
A
B
C
∵△A′B′C′是由△ABC旋转得到的,
∴OA= OA′、OB=OB′、OC=OC′
∠AOA′=∠BOB′=∠COC′, ABC≌ A′B′C′
7
巩固练习
知识点一:旋转及其性质
1.两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为 ,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分的面积是否发生变化 请说明理由.
A
B
D
O
E
E′
D′
A
B
D
O
E
8
巩固练习
知识点一:旋转及其性质
2.如图,在□ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
A.130° B.150° C.160° D.170°
A
B
D
E
C
E′
A′
∟
∟
C
9
巩固练习
知识点一:旋转及其性质
3.如图,在Rt△ABC中,∠B=90°AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .
4.如图,在Rt△ABC中∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在斜边AB上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A.30,2 B.60,2 C.60, D.60,
A
B
C
D
E
F
C
A
B
C
D
E
∟
10
巩固练习
知识点一:旋转及其性质
5.在如图的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为 ( )
A.(4,1) B.(4,-1)C.(5, 1) D.(5,-1)
D
11
巩固练习
知识点一:旋转及其性质
5.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
A.30° B.60°
C.90° D.120°
C
12
知识回顾
知识点二:中心对称及中心对称图形
“中心对称与轴对称的对比”
中心对称 轴对称
不同点
相同点
图形绕对称中心旋转180° 图形沿对称轴折叠
图形旋转后与另一个图形重合 图形折叠后与另一个图形重合
对称中心只有一个 至少有一条对称轴
都是两个图形之间的关系,而且变换前、后两个图形全等
13
知识回顾
知识点二:中心对称及中心对称图形
O
A
B
C
A′
B′
C′
1.中心对称的两个图形,对称点所连线段都经过 ,而且被 所平分。
2.关于中心对称的两个图形是 。
中心对称的性质:
对称中心
对称中心
全等形
几何语言
∵ ABC和 A′B′C′关于点O成中心对称
∴OA=OA′,OB=OB′,OC=OC′
ABC≌ A′B′C′
14
知识回顾
知识点二:中心对称及中心对称图形
中心对称图形 轴对称图形
区别
举例
中心对称图形与轴对称图形的对比
(1)是关于某一点对称 (1)是某一条直线对称
(2)是绕某一点旋转180°后与原来的图象重合
线段、平行四边形、矩形、菱形、边数是偶数的正多边形、圆等都是中心对称图形
线段、角、等腰三角形、矩形、菱形、正多边形等都是轴对称图形
(2)是沿一条直线折叠后,直线两旁的部分互相重合
15
知识回顾
知识点二:中心对称及中心对称图形
中心对称 中心对称图形
区别
联系
中心对称与中心对称图形的区别和联系
(1)是针对两个图形而言的 (1)是针对一个图形而言的
(2)是指两个图形的(位置)关系 (2)是指具有某种性质的一个图形
(3)对称点在两个图形上 (3)对称点在一个图形上
(4)对称中心可能在两个图形的外部,(4)对称中心在图形内部.
也可能在图形的内部或图形上.
(1)都是根据把图形旋转180°后能重合定义的.
(2)两者可以相互转化,若把成中心对称的两个图形视为一个整体,则整个图形是中心对称图形;若把一个中心对称图形相互对称的两部分看作两个图形,则这两个图形成中心对称
16
知识回顾
知识点二:中心对称及中心对称图形
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分.即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等)
中心对称图形的性质
17
巩固练习
知识点二:中心对称及中心对称图形
1.下列说法中,①线段两端点关于它的中点对称;
②菱形一组对边关于对角线交点对称;
③成中心对称的两个图形一定全等;
④如果两个图形全等,那么这两个图形一定关于某点成中心对称;
⑤如果两个三角形的对应点连线都经过一点,那么这两个三角形成中心对称.其中正确的有 (填序号).
①②③
18
巩固练习
知识点二:中心对称及中心对称图形
2.如图,在Rt△ABC中,斜边AB长为 ,直角边BC长为12,若扇形ACE与扇形BDE关于点E成中心对称,则图中阴影部分的面积为 .
19
巩固练习
知识点二:中心对称及中心对称图形
B
3.下列所述图形中,是中心对称图形的是( )
A直角三角形 B.平行四边形 C.正五边形 D.正三角形
4.下列图形:①圆;②正五边形;③正方形:④抛物线y=x2其中既是中心对称图形又是轴对称图形的是 (填序号)
5.右图中,中心对
称图形有( )
A.4个B.3个C.2个,D.1个
①③
B
20
巩固练习
知识点二:中心对称及中心对称图形
6.如图,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD,BC分别交于点E,F,则图中相等的线段有( )
A.3对 B.4对 C.5对 D.6对
7.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为 .
A
B
D
C
O
E
F
21
巩固练习
知识点二:中心对称及中心对称图形
8.如图所示的放置着两个矩形,请你作一条直线,将此图形分成面积相等的两部分.(不写作法,保留作图痕迹)
22
知识回顾
知识点三:关于原点对称的点的坐标
两个点关于原点对称时,
它们的坐标符号相反,
即点P(x,y)关于原点的对称点为P′(﹣x,﹣y).
A
B
C
D
E
A′
B′
C′
D′
E′
(2,1)
(-2,-1)
23
知识回顾
知识点三:关于原点对称的点的坐标
名 称 区 别 举 例
关于坐标轴对称 关于x轴对称
关于y轴对称
关于原点对称
横坐标相等,
纵坐标互为相反数.
点P(x,y)关于x轴对称的点P1为(x,-y).
纵坐标相等,
横坐标互为相反数.
点P(x,y)关于y轴对称的点P2为(-x,y).
纵,横坐标分别互为相反数.
点P(x,y)关于原点对称的点P3为(-x,-y).
24
知识回顾
知识点三:关于原点对称的点的坐标
两个点关于直线y=x对称时,
它们的坐标互换,
即点P(x,y)关于直线y=x的对称点为P1(y,x).
A
B
C
D
E
A′
B′
C′
D′
E′
(2,1)
(1,2)
25
知识回顾
知识点三:关于原点对称的点的坐标
两个点关于直线y= - x对称时,
它们的纵横坐标互换且符号改变,
即点P(x,y)关于直线y= - x的对称点为P2(-y,-x).
A
B
C
D
E
A′′
B′′
C′′
D′′
E′′
(2,1)
(-1,-2)
26
知识回顾
知识点三:关于原点对称的点的坐标
①P(x,y)
设点P的坐标为(x,y),那么有下列结论:
关于x轴对称
P(x,-y)
②P(x,y)
关于y轴对称
P(-x,y)
③P(x,y)
关于y=x对称
P(y,x)
④P(x,y)
关于y=-x对称
P(-y,-x)
⑤P(x,y)
关于原点对称
P(-x,-y)
27
巩固练习
知识点三:关于原点对称的点的坐标
1.点P(-2,3)关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.将点A(3,2)沿y轴正方向平移3个单位长度得到点B,则点B关于原点的对称点的坐标为( )
A.(3,5) B.(5,3) C.(-3,-5) D.(-5,-3)
3.已知点A(a,-3)与点A′(5,b)关于坐标原点对称,则实数a,b的值是( )
A.a=5.b=3 B.a=-5.b=-3 C.a=5,b=-3 D.a=-5.b=3
D
C
D
28
巩固练习
知识点三:关于原点对称的点的坐标
4.点P(-2,3)关于直线y=x对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.将点A(3,2)沿y轴正方向平移3个单位长度得到点B,则点B关于直线y=-x的对称点的坐标为( )
A.(3,5) B.(5,3) C.(-3,-5) D.(-5,-3)
6.已知点A(a,-3)与点A′(b,5)关于直线y=-x对称,则实数a,b的值是( )
A.a=5.b=3 B.a=-5.b=-3 C.a=5,b=-3 D.a=-5.b=3
D
D
D
29
巩固练习
知识点三:关于原点对称的点的坐标
7.已知点P(a+1,- +1)关于原点的对称点在第四象限,则a的取值范围是 .
8.(易错题)已知△ABC的三边长分别为a,b,c,且满足点A(∣2c-16∣,(a- )2)与点B( ,-32)关于原点对称,则△ABC的形状是 .
9.已知点P(1-2a,a-2)关于原点的对称点在第一象限内,且a为整数,则关于x的分式方程 =-1的解是 .
x<-1
等腰直角三角形
30
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心;
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
确定对称中心的方法
知识回顾
知识点四:平移、旋转、轴对称作图
31
作已知图形关于某一点对称的图形,其作图步骤简记为:连接、延长、截取相等线段、连点成图.
在平面直角坐标系中作已知图形关于某一点对称的图形有没有其他方法?
知识回顾
知识点四:平移、旋转、轴对称作图
32
知识回顾
知识点四:平移、旋转、轴对称作图
图案设计:图案设计的变换组合一般有以下几种
(1)先平移后旋转;
(2)先旋转后平移;
(3)先转后作轴对称
(4)先作轴对称后平移
33
巩固练习
知识点二:中心对称及中心对称图形
1、如图,在平面直角坐标系中,△ABC各顶点的坐标分别为
A(-2,-2),B(-4,-1),C(-4,-4).作出△ABC关于原点0对称的△A1B1C1并写出点A1,B1,C1的坐标.
O
A
B
C
y
x
A1
B1
C1
34
巩固练习
知识点四:平移、旋转、轴对称作图
2.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
35
巩固练习
知识点四:平移、旋转、轴对称作图
3.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.1种 B.2种 C.3种 D.4种
36
思维导图
37
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
同课章节目录
