人教版七年级数学上册 第四章 几何图形初步单元检测试卷(含解析)
文档属性
| 名称 | 人教版七年级数学上册 第四章 几何图形初步单元检测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 172.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 13:43:32 | ||
图片预览



文档简介
第四章 几何图形初步单元检测试卷
一.选择题(本大题共10小题,每小题3分,共30分)
1.下列语句中,正确的个数是( )
①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.
A.1个 B.2个 C.3个 D.4个
2.观察下列图形,其中不是正方体的表面展开图的是( )
A B C D
3.用度、分、秒表示21.24°为( )
A.21°14'24″ B.21°20'24″ C.21°34' D.21°
4.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )
A B C D
5.如图,点O在直线AB上,若∠AOC=30°,则∠BOC的度数是( )
A.60° B.70° C.140° D.150°
6.如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD上,且EA=1,则BE的长为( )
A.4 B.6或8 C.6 D.8
7.某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
8.2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动.宜传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体中,与汉字“抗”相对的面上的汉字是( )
A.共 B.同 C.疫 D.情
9.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°;②若∠1+∠2=90°,则∠1和∠2互为余角;③若∠1+∠2+∠3=180°,则∠1,∠2和∠3互为补角;④一个角的补角必为钝角.
A.①② B.①②③ C.②③④ D.③④
10.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种 B.8种 C.9种 D.6种
二.填空题(本大题共8小题,每小题3分,共24分)
11.计算:65°19′48″+35°17′6″= (将计算结果换算成度).
12.一个角的补角与它的余角的3倍的差是40°,则这个角为 .
13.小张家里的挂钟指向9:30,此时该挂钟的时针与分针所夹的角是 .
14.已知点A,B,C在一条直线上,AB=5cm,BC=3cm,则AC的长为 .
15.一副三角尺按如图方式摆放,且∠1的度数比∠2的度数大50°,则∠2= .
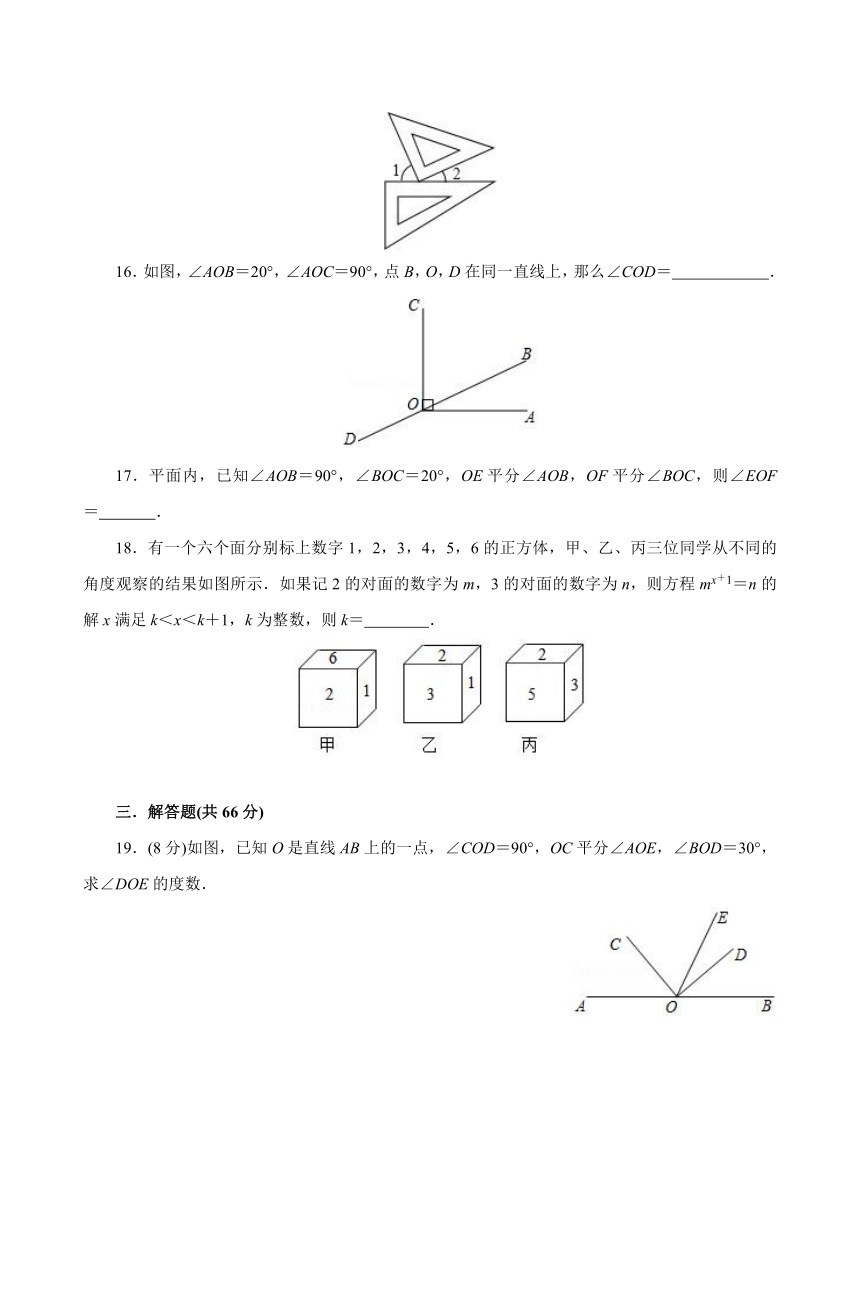
16.如图,∠AOB=20°,∠AOC=90°,点B,O,D在同一直线上,那么∠COD= .
17.平面内,已知∠AOB=90°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF= .
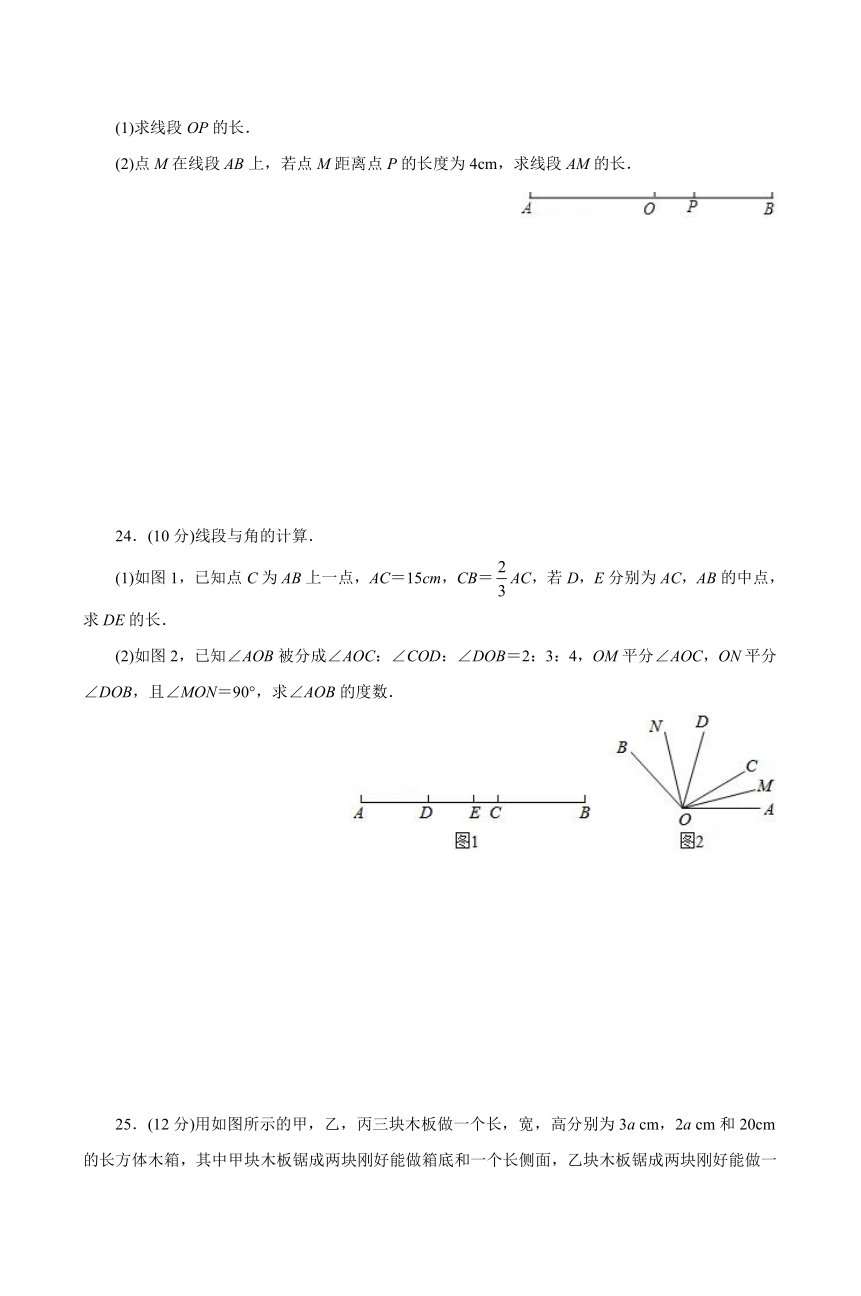
18.有一个六个面分别标上数字1,2,3,4,5,6的正方体,甲、乙、丙三位同学从不同的角度观察的结果如图所示.如果记2的对面的数字为m,3的对面的数字为n,则方程mx+1=n的解x满足k<x<k+1,k为整数,则k= .
三.解答题(共66分)
19.(8分)如图,已知O是直线AB上的一点,∠COD=90°,OC平分∠AOE,∠BOD=30°,求∠DOE的度数.
20.(8分)如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
21.(9分)如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠BOE的度数.
22.(9分)一个圆柱体,如果把它的高截短3分米,它的表面积就减少18.84平方分米,这个圆柱的体积减少了多少立方分米?要把截下的高3分米的圆柱部分漆上油漆,要漆多少平方分米?
23.(10分)点O是线段AB的中点,OB=14cm,点P将线段AB分为两部分,AP:PB=5:2.
(1)求线段OP的长.
(2)点M在线段AB上,若点M距离点P的长度为4cm,求线段AM的长.
24.(10分)线段与角的计算.
(1)如图1,已知点C为AB上一点,AC=15cm,CB=AC,若D,E分别为AC,AB的中点,求DE的长.
(2)如图2,已知∠AOB被分成∠AOC:∠COD:∠DOB=2:3:4,OM平分∠AOC,ON平分∠DOB,且∠MON=90°,求∠AOB的度数.
25.(12分)用如图所示的甲,乙,丙三块木板做一个长,宽,高分别为3a cm,2a cm和20cm的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板锯成两块刚好能做一个长侧面和一个短侧面,丙块木板锯成两块刚好能做箱盖和剩下的一个短侧面(厚度忽略不计).
(1)用含a的代数式分别表示甲,乙,丙三块木板的面积(代数式要求化简);
(2)如果购买一块长12a cm,宽120cm的长方形木板做这个箱子,那么只需用去这块木板的几分之几(用含a的代数式表示)?如果a=20呢?
参考答案
1. 【答案】C 【解析】①直线AB和直线BA是一条直线,原来的说法是错误的;②射线AB和射线BA是两条射线是正确的;③互余是指的两个角的关系,原来的说法是错误的;④一个角的余角比这个角的补角小是正确的;⑤周角的特点是两条边重合成射线.但不能说成周角是一条射线,原来的说法是错误的;⑥两点之间,线段最短是正确的.故正确的个数是3个.
2. 【答案】B 【解析】选项A、C、D均是正方体表面展开图;选项B是凹字格,故不是正方体表面展开图.
3. 【答案】A 【解析】21.24°=21°+0.24×60′=21°+14′+0.4×60″=21°14′24″.
4. 【答案】C 【解析】以直线为轴旋转一周可以得到圆锥,故选项A不合题意;以直线为轴旋转一周可以得到两个圆锥,故选项B不合题意;以直线为轴旋转一周可以得到圆柱,故选项C符合题意;以直线为轴旋转一周可以得到球,故选项D不合题意;故选C.
5. 【答案】D 【解析】∵∠AOC与∠BOC互为邻补角,∴∠AOC+∠BOC=180°,又∵∠AOC=30°,∴∠BOC=180°﹣∠AOC=180°﹣30°=150°.
6. 【答案】B 【解析】若E在线段DA的延长线,如图1,∵EA=1,AD=9,∴ED=EA+AD=1+9=10,∵BD=2,∴BE=ED﹣BD=10﹣2=8,若E线段AD上,如图2,EA=1,AD=9,∴ED=AD﹣EA=9﹣1=8,∵BD=2,∴BE=ED﹣BD=8﹣2=6,综上所述,BE的长为8或6.
7. 【答案】B 【解析】如图所示,
∵某人在A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,∴∠BAD=40°,∠CAD=35°,∴∠BAC=∠BAD+∠CAD=40°+35°=75°.
8. 【答案】D 【解析】根据正方体展开图的特征,“相间、Z端是对面”可得,“抗”的对面是“情”,故选D.
9. 【答案】A 【解析】①已知∠A=40°,则∠A的余角是50°,原说法正确;②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;④一个角的补角不一定是钝角,原说法错误.说法正确的是①②.
10. 【答案】A 【解析】由题意可得:
他能漆成互不相同的立方体的种数是10.
11. 【答案】100.615° 【解析】65°19′48″+35°17′6″=100°36′54″,∵54÷60=0.9,(36+0.9)÷60=0.615,100+0.615=100.615,∴100°36′54″=100.615°.
12. 【答案】65° 【解析】设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有180﹣x﹣3(90﹣x)=40,解得x=65.故这个角是65°.
13. 【答案】105° 【解析】3×30°+15°=105°.∴钟面上9点30分时,分针与时针所成的角的度数是105°.
14. 【答案】2cm或8cm 【解析】若C在线段AB上,
则AC=AB﹣BC=5﹣3=2(cm);若C在线段AB的延长线上,
则AC=AB+BC=5+3=8(cm),故答案为2cm或8cm.
15. 【答案】20° 【解析】由图可知:∠1+∠2+90°=180°,即∠1+∠2=90°,∵∠1﹣∠2=50°,∴∠1=70°,∠2=20°.
16. 【答案】110° 【解析】∵∠AOB=20°,∠AOC=90°,∴∠BOC=70°,∴∠DOC=180°﹣70°=110°.
17. 【答案】35°或55° 【解析】当OC在∠AOB内时,如图1,
∠EOF=∠BOE﹣∠BOF=∠AOB﹣∠BOC=×90°﹣×20°=35°;当OC在∠AOB外时,如图2,∠EOF=∠BOE+∠BOF=∠AOB+∠BOC=×90°+×20°=55°.
18. 【答案】0 【解析】从图可以看出2和6,1,3,2都相邻,所以2的对面只能是4,即m=4;3和1,2,5,3相邻,那么3的对面是6,即n=6;∵mx+1=n,∴4x+1=6,∴1<x+1<2,∵k<x<k+1,k为整数,∴k=0.
19. 解:∵∠BOD=30°,∠COD=90°,∴∠AOC=90°﹣∠BOD=60°.∵OC平分∠AOE,∴∠COE=∠AOE=60°.∴∠DOE=∠COD﹣∠COE=30°.
20. 解:(1)AC=9,BC=6,则AB=AC=BC=9+6=15,∵AM=2MC,BN=2NC.∴MC=AC,NC=BC,∴MN=MC+NC=(AC+BC)=AB=×15=5,答:MN的长为5;
(2)由(1)得,MN═AB,若MN=5时,AB=15,答:AB的长为15.
21. 解:设∠DOE=2x,∵∠DOE:∠BOD=2:5,∴∠BOE=3x,又∵OC是∠AOD的平分线,∠COE=80°,∴∠AOC=∠COD=80°﹣2x,2×(80°﹣2x)+5x=180°,解得x=20°,∴∠BOE=3x=3×20°=60°.
22. 解:18.84÷3=6.28(分米),6.28÷3.14÷2=1(分米),3.14×12×3=9.42(立方分米),3.14×12×2+18.84=25.12(平方分米).答:这个圆柱的体积减少了9.42立方分米,要漆25.12平方分米.
23. 解:(1)∵点O是线段AB的中点,OB=14cm,∴AB=2OB=28cm,∵AP:PB=5:2.∴BP=AB=8cm,∴OP=OB﹣BP=14﹣8=6(cm);
(2)如图1,当M点在P点的左边时,
AM=AB﹣(PM+BP)=28﹣(4+8)=16(cm),如图2,当M点在P点的右边时,AM=AB﹣BM=AB﹣(BP﹣PM)=28﹣(8﹣4)=24(cm).综上,AM=16cm或24cm.
24. 解:(1)∵AC=15cm,CB=AC,∴CB=×15=10(cm),∴AB=15+10=25(cm).∵D,E分别为AC,AB的中点,∴AE=BE=AB=12.5cm,DC=AD=AC=7.5cm,∴DE=AE﹣AD=12.5﹣7.5=5(cm);
(2)设∠AOC=2x,∠COD=3x,∠DOB=4x,则∠AOB=9x,∵OM平分∠AOC,ON平分∠DOB,∴∠MOC=x,∠NOD=2x,∴∠MON=x+3x+2x=6x,又∵∠MON=90°,∴6x=90°,∴x=15°,∴∠AOB=135°.
25. 解:(1)由题意得,甲木板的面积:3a×2a+3a×20=(6a2+60a)(cm2),乙木板的面积:3a×20+2a×20=100a(cm2),丙木板的面积:3a×2a+2a×20=(6a2+40a)(cm2);
(2)长12a cm,宽120cm的长方形木板的面积:12a×120=1440a,=,当a=20时,==.答:需用去这块木板的,当a=20时,用去这块木板的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
一.选择题(本大题共10小题,每小题3分,共30分)
1.下列语句中,正确的个数是( )
①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.
A.1个 B.2个 C.3个 D.4个
2.观察下列图形,其中不是正方体的表面展开图的是( )
A B C D
3.用度、分、秒表示21.24°为( )
A.21°14'24″ B.21°20'24″ C.21°34' D.21°
4.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )
A B C D
5.如图,点O在直线AB上,若∠AOC=30°,则∠BOC的度数是( )
A.60° B.70° C.140° D.150°
6.如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD上,且EA=1,则BE的长为( )
A.4 B.6或8 C.6 D.8
7.某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
8.2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动.宜传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体中,与汉字“抗”相对的面上的汉字是( )
A.共 B.同 C.疫 D.情
9.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°;②若∠1+∠2=90°,则∠1和∠2互为余角;③若∠1+∠2+∠3=180°,则∠1,∠2和∠3互为补角;④一个角的补角必为钝角.
A.①② B.①②③ C.②③④ D.③④
10.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种 B.8种 C.9种 D.6种
二.填空题(本大题共8小题,每小题3分,共24分)
11.计算:65°19′48″+35°17′6″= (将计算结果换算成度).
12.一个角的补角与它的余角的3倍的差是40°,则这个角为 .
13.小张家里的挂钟指向9:30,此时该挂钟的时针与分针所夹的角是 .
14.已知点A,B,C在一条直线上,AB=5cm,BC=3cm,则AC的长为 .
15.一副三角尺按如图方式摆放,且∠1的度数比∠2的度数大50°,则∠2= .
16.如图,∠AOB=20°,∠AOC=90°,点B,O,D在同一直线上,那么∠COD= .
17.平面内,已知∠AOB=90°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF= .
18.有一个六个面分别标上数字1,2,3,4,5,6的正方体,甲、乙、丙三位同学从不同的角度观察的结果如图所示.如果记2的对面的数字为m,3的对面的数字为n,则方程mx+1=n的解x满足k<x<k+1,k为整数,则k= .
三.解答题(共66分)
19.(8分)如图,已知O是直线AB上的一点,∠COD=90°,OC平分∠AOE,∠BOD=30°,求∠DOE的度数.
20.(8分)如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
21.(9分)如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠BOE的度数.
22.(9分)一个圆柱体,如果把它的高截短3分米,它的表面积就减少18.84平方分米,这个圆柱的体积减少了多少立方分米?要把截下的高3分米的圆柱部分漆上油漆,要漆多少平方分米?
23.(10分)点O是线段AB的中点,OB=14cm,点P将线段AB分为两部分,AP:PB=5:2.
(1)求线段OP的长.
(2)点M在线段AB上,若点M距离点P的长度为4cm,求线段AM的长.
24.(10分)线段与角的计算.
(1)如图1,已知点C为AB上一点,AC=15cm,CB=AC,若D,E分别为AC,AB的中点,求DE的长.
(2)如图2,已知∠AOB被分成∠AOC:∠COD:∠DOB=2:3:4,OM平分∠AOC,ON平分∠DOB,且∠MON=90°,求∠AOB的度数.
25.(12分)用如图所示的甲,乙,丙三块木板做一个长,宽,高分别为3a cm,2a cm和20cm的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板锯成两块刚好能做一个长侧面和一个短侧面,丙块木板锯成两块刚好能做箱盖和剩下的一个短侧面(厚度忽略不计).
(1)用含a的代数式分别表示甲,乙,丙三块木板的面积(代数式要求化简);
(2)如果购买一块长12a cm,宽120cm的长方形木板做这个箱子,那么只需用去这块木板的几分之几(用含a的代数式表示)?如果a=20呢?
参考答案
1. 【答案】C 【解析】①直线AB和直线BA是一条直线,原来的说法是错误的;②射线AB和射线BA是两条射线是正确的;③互余是指的两个角的关系,原来的说法是错误的;④一个角的余角比这个角的补角小是正确的;⑤周角的特点是两条边重合成射线.但不能说成周角是一条射线,原来的说法是错误的;⑥两点之间,线段最短是正确的.故正确的个数是3个.
2. 【答案】B 【解析】选项A、C、D均是正方体表面展开图;选项B是凹字格,故不是正方体表面展开图.
3. 【答案】A 【解析】21.24°=21°+0.24×60′=21°+14′+0.4×60″=21°14′24″.
4. 【答案】C 【解析】以直线为轴旋转一周可以得到圆锥,故选项A不合题意;以直线为轴旋转一周可以得到两个圆锥,故选项B不合题意;以直线为轴旋转一周可以得到圆柱,故选项C符合题意;以直线为轴旋转一周可以得到球,故选项D不合题意;故选C.
5. 【答案】D 【解析】∵∠AOC与∠BOC互为邻补角,∴∠AOC+∠BOC=180°,又∵∠AOC=30°,∴∠BOC=180°﹣∠AOC=180°﹣30°=150°.
6. 【答案】B 【解析】若E在线段DA的延长线,如图1,∵EA=1,AD=9,∴ED=EA+AD=1+9=10,∵BD=2,∴BE=ED﹣BD=10﹣2=8,若E线段AD上,如图2,EA=1,AD=9,∴ED=AD﹣EA=9﹣1=8,∵BD=2,∴BE=ED﹣BD=8﹣2=6,综上所述,BE的长为8或6.
7. 【答案】B 【解析】如图所示,
∵某人在A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,∴∠BAD=40°,∠CAD=35°,∴∠BAC=∠BAD+∠CAD=40°+35°=75°.
8. 【答案】D 【解析】根据正方体展开图的特征,“相间、Z端是对面”可得,“抗”的对面是“情”,故选D.
9. 【答案】A 【解析】①已知∠A=40°,则∠A的余角是50°,原说法正确;②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;④一个角的补角不一定是钝角,原说法错误.说法正确的是①②.
10. 【答案】A 【解析】由题意可得:
他能漆成互不相同的立方体的种数是10.
11. 【答案】100.615° 【解析】65°19′48″+35°17′6″=100°36′54″,∵54÷60=0.9,(36+0.9)÷60=0.615,100+0.615=100.615,∴100°36′54″=100.615°.
12. 【答案】65° 【解析】设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有180﹣x﹣3(90﹣x)=40,解得x=65.故这个角是65°.
13. 【答案】105° 【解析】3×30°+15°=105°.∴钟面上9点30分时,分针与时针所成的角的度数是105°.
14. 【答案】2cm或8cm 【解析】若C在线段AB上,
则AC=AB﹣BC=5﹣3=2(cm);若C在线段AB的延长线上,
则AC=AB+BC=5+3=8(cm),故答案为2cm或8cm.
15. 【答案】20° 【解析】由图可知:∠1+∠2+90°=180°,即∠1+∠2=90°,∵∠1﹣∠2=50°,∴∠1=70°,∠2=20°.
16. 【答案】110° 【解析】∵∠AOB=20°,∠AOC=90°,∴∠BOC=70°,∴∠DOC=180°﹣70°=110°.
17. 【答案】35°或55° 【解析】当OC在∠AOB内时,如图1,
∠EOF=∠BOE﹣∠BOF=∠AOB﹣∠BOC=×90°﹣×20°=35°;当OC在∠AOB外时,如图2,∠EOF=∠BOE+∠BOF=∠AOB+∠BOC=×90°+×20°=55°.
18. 【答案】0 【解析】从图可以看出2和6,1,3,2都相邻,所以2的对面只能是4,即m=4;3和1,2,5,3相邻,那么3的对面是6,即n=6;∵mx+1=n,∴4x+1=6,∴1<x+1<2,∵k<x<k+1,k为整数,∴k=0.
19. 解:∵∠BOD=30°,∠COD=90°,∴∠AOC=90°﹣∠BOD=60°.∵OC平分∠AOE,∴∠COE=∠AOE=60°.∴∠DOE=∠COD﹣∠COE=30°.
20. 解:(1)AC=9,BC=6,则AB=AC=BC=9+6=15,∵AM=2MC,BN=2NC.∴MC=AC,NC=BC,∴MN=MC+NC=(AC+BC)=AB=×15=5,答:MN的长为5;
(2)由(1)得,MN═AB,若MN=5时,AB=15,答:AB的长为15.
21. 解:设∠DOE=2x,∵∠DOE:∠BOD=2:5,∴∠BOE=3x,又∵OC是∠AOD的平分线,∠COE=80°,∴∠AOC=∠COD=80°﹣2x,2×(80°﹣2x)+5x=180°,解得x=20°,∴∠BOE=3x=3×20°=60°.
22. 解:18.84÷3=6.28(分米),6.28÷3.14÷2=1(分米),3.14×12×3=9.42(立方分米),3.14×12×2+18.84=25.12(平方分米).答:这个圆柱的体积减少了9.42立方分米,要漆25.12平方分米.
23. 解:(1)∵点O是线段AB的中点,OB=14cm,∴AB=2OB=28cm,∵AP:PB=5:2.∴BP=AB=8cm,∴OP=OB﹣BP=14﹣8=6(cm);
(2)如图1,当M点在P点的左边时,
AM=AB﹣(PM+BP)=28﹣(4+8)=16(cm),如图2,当M点在P点的右边时,AM=AB﹣BM=AB﹣(BP﹣PM)=28﹣(8﹣4)=24(cm).综上,AM=16cm或24cm.
24. 解:(1)∵AC=15cm,CB=AC,∴CB=×15=10(cm),∴AB=15+10=25(cm).∵D,E分别为AC,AB的中点,∴AE=BE=AB=12.5cm,DC=AD=AC=7.5cm,∴DE=AE﹣AD=12.5﹣7.5=5(cm);
(2)设∠AOC=2x,∠COD=3x,∠DOB=4x,则∠AOB=9x,∵OM平分∠AOC,ON平分∠DOB,∴∠MOC=x,∠NOD=2x,∴∠MON=x+3x+2x=6x,又∵∠MON=90°,∴6x=90°,∴x=15°,∴∠AOB=135°.
25. 解:(1)由题意得,甲木板的面积:3a×2a+3a×20=(6a2+60a)(cm2),乙木板的面积:3a×20+2a×20=100a(cm2),丙木板的面积:3a×2a+2a×20=(6a2+40a)(cm2);
(2)长12a cm,宽120cm的长方形木板的面积:12a×120=1440a,=,当a=20时,==.答:需用去这块木板的,当a=20时,用去这块木板的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
