人教版七年级数学上册课件4.3.1 角 课件(共24张PPT)
文档属性
| 名称 | 人教版七年级数学上册课件4.3.1 角 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 13:52:10 | ||
图片预览







文档简介
(共24张PPT)
4.3 角
4.3.1 角
1.认识角是一种基本的几何图形,理解角的概念,学会角的表示方法.(重点)
2.了解角的度量单位度、分、秒,会进行简单的换算和角度计算.(重点、难点)
1.角的概念的两种表述
(1)角是有公共端点的两条_____组成的图形,其中公共端点
是角的_____,_________是角的边.
(2)角是由一条_____绕着它的端点旋转而形成的图形.
射线
顶点
两条射线
射线
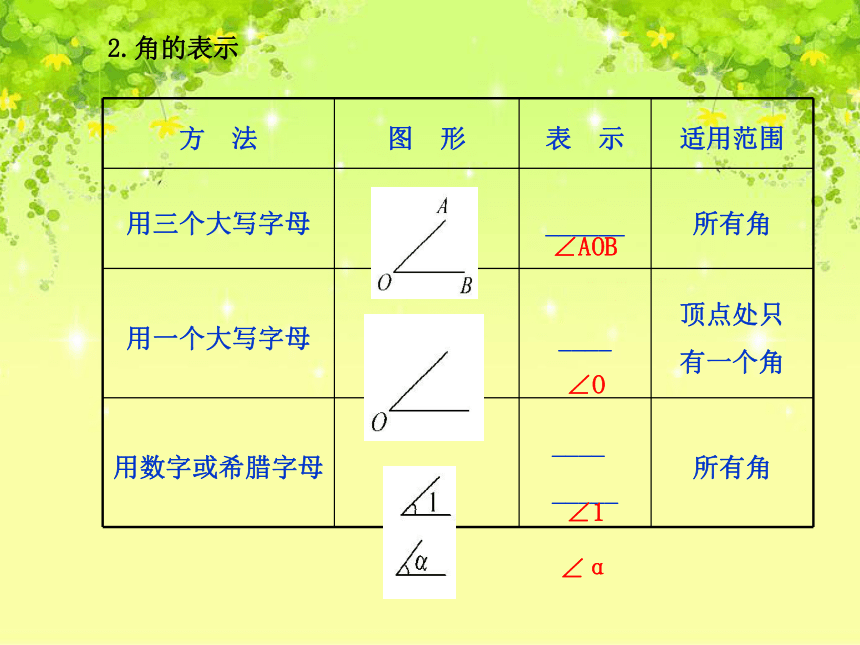
方 法 图 形 表 示 适用范围
用三个大写字母 ______ 所有角
用一个大写字母 ____ 顶点处只
有一个角
用数字或希腊字母 ____
_____ 所有角
2.角的表示
∠AOB
∠O
∠1
∠α
3.角的度量
(1)角的度量单位:___、___、___.
(2)度分秒的换算:1°=_____,1′=_____.
(3)1周角=______,1平角=______.
度
分
秒
60′
60″
180°
360°
(打“√”或“×”)
(1)一个角的边越长角越大.( )
(2)所有角都能用顶点的大写字母表示.( )
(3)平角就是直线.( )
(4)角的度、分、秒之间的换算与时间的时、分、秒一样都是
60进制.( )
×
×
×
√
知识点 1 角的识别与表示
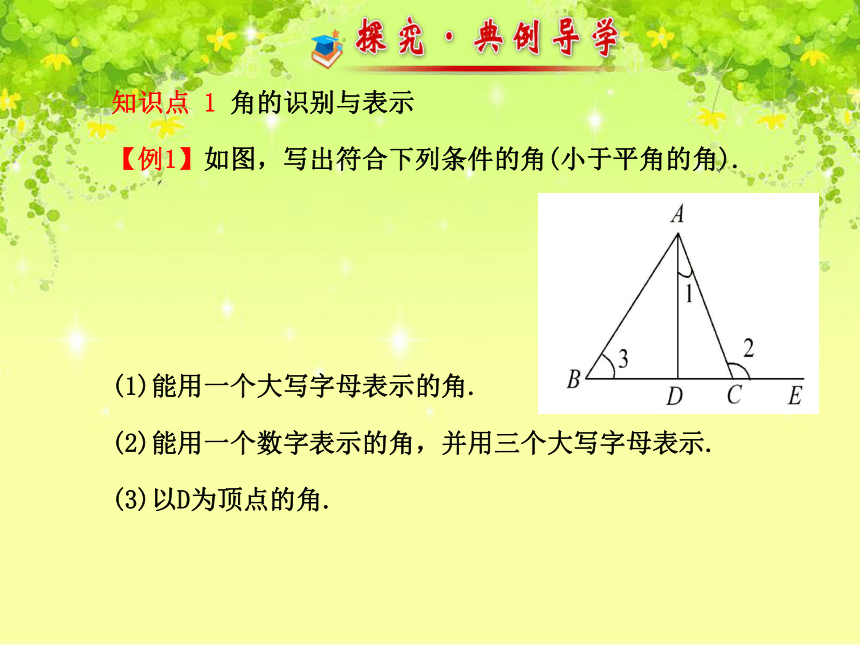
【例1】如图,写出符合下列条件的角(小于平角的角).
(1)能用一个大写字母表示的角.
(2)能用一个数字表示的角,并用三个大写字母表示.
(3)以D为顶点的角.
【思路点拨】(1)以某点为顶点的角只有一个时才能用一个大写字母表示.
(2)找出标有数字的角,并用三个大写字母表示.
(3)找以D为端点的射线(或线段)形成的角,并用三个字母表示.
【自主解答】(1)顶点处只有一个角的为∠B,所以能用一个大写字母表示的角为∠B.
(2)∠1用三个大写字母表示为∠CAD, ∠2用三个大写字母表示为∠ACE, ∠3用三个大写字母表示为∠ABD.
(3)∠ADC,∠ADB.
【总结提升】表示角时注意的三点
1.用三个字母表示角时,顶点字母必须写在中间.
2.用一个字母表示角时,必须顶点处只有一个角.
3.用数字或希腊字母表示角时,必须在相应角的内部加弧线及数字或希腊字母.
知识点 2 角的度、分、秒的换算
【例2】(1)把4.62°化成度、分、秒.
(2)把45°23′45″化成度.
【教你解题】
【总结提升】度、分、秒相互换算的法则
1.度、分、秒的换算是60进制.
2.角的度数的换算有两种情况:
(1)把度化成度、分、秒的形式,即从高单位向低单位转化时,每级变化乘以60.
(2)把度、分、秒化成度的形式,即从低单位向高单位转化时,每级变化除以60.
题组一:角的识别与表示
1.下列关于角的说法正确的是( )
A.两条射线组成的图形叫做角
B.延长一个角的两边
C.角的两边是射线,所以角不可以度量
D.角的大小与这个角的两边长短无关
【解析】选D.形成角的两条射线应有公共端点,A不正确;角的边是射线不能延长,B不正确;角的大小是指两边张开的幅度,可以度量,与边的长短无关,C不正确.
2.下图中表示∠ABC的图是( )
【解析】选C.选项A为∠CAB,选项B不是角;选项D为∠ACD.
3.如图所示,下列表示角的方法中错
误的是( )
A.∠1与∠AOB表示同一个角
B.∠AOC也可以用∠O来表示
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠β表示的是∠BOC
【解析】选B.以O为顶点的角有三个,不能用一个大写字母来表示.
4.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
【解析】选D.前三个选项以O为顶点的角都不止一个,所以都不能用一个大写字母来表示 .
5.写出如图所示的符合下列条件的角(图中
所有的角指小于平角的角).
(1)能用一个大写字母表示的角.
(2)以A为顶点的角.
(3)图中所有的角(可用简便方法表示).
【解析】(1)∠B,∠C.
(2)∠1或∠CAD,∠2或∠DAB,∠CAB.
(3)∠C,∠1,∠2,∠CAB,∠B,∠3,∠4.
题组二:角的度、分、秒的换算
1.14时的钟表的时针与分针所形成的角的度数是( )
A.30° B.45°
C.60° D.90°
【解析】选C.钟表的1个大格是 周角=30°,14时的时针与
分针形成的角是2个大格,故为60°.
2.(1)3.76°=________度________分________秒.
(2)3.76°=________分=________秒.
【解析】(1)0. 76°=0.76×60=45.6′,0.6′=0.6×60=36″,所以3.76°=3°45′36″.(2) 3.76°=3.76×60=225.6′,225.6′=225.6×60=13 536″.
答案:(1)3 45 36
(2)225.6 13 536
3.把35°24′36″化成用度表示的形式.
【解析】因为36″=36÷60=0.6′,所以24′36″=24.6′=
24.6÷60=0.41°,所以35°24′36″=35.41°.
4.32°18′与32.18°哪个大?
【解析】方法一:因为32°18′=32.3°,32.3°>32.18°,
所以32°18′>32.18°.
方法二:因为0. 18°=10.8′,所以32.18°=32°10.8′,又因为32°18′>32°10.8′,所以32°18′>32.18°.
5.如图,分别确定四个城市相应钟表上时针与分针所成角的度数(小于平角的角).
【解析】巴黎:30°,伦敦:0°,北京:30°×4=120°,东京:30°×3=90°.
【想一想错在哪?】钟表上3时30分的时针与分针的夹角是多少?
提示:要弄清时针、分针特别是时针所在的位置.
4.3 角
4.3.1 角
1.认识角是一种基本的几何图形,理解角的概念,学会角的表示方法.(重点)
2.了解角的度量单位度、分、秒,会进行简单的换算和角度计算.(重点、难点)
1.角的概念的两种表述
(1)角是有公共端点的两条_____组成的图形,其中公共端点
是角的_____,_________是角的边.
(2)角是由一条_____绕着它的端点旋转而形成的图形.
射线
顶点
两条射线
射线
方 法 图 形 表 示 适用范围
用三个大写字母 ______ 所有角
用一个大写字母 ____ 顶点处只
有一个角
用数字或希腊字母 ____
_____ 所有角
2.角的表示
∠AOB
∠O
∠1
∠α
3.角的度量
(1)角的度量单位:___、___、___.
(2)度分秒的换算:1°=_____,1′=_____.
(3)1周角=______,1平角=______.
度
分
秒
60′
60″
180°
360°
(打“√”或“×”)
(1)一个角的边越长角越大.( )
(2)所有角都能用顶点的大写字母表示.( )
(3)平角就是直线.( )
(4)角的度、分、秒之间的换算与时间的时、分、秒一样都是
60进制.( )
×
×
×
√
知识点 1 角的识别与表示
【例1】如图,写出符合下列条件的角(小于平角的角).
(1)能用一个大写字母表示的角.
(2)能用一个数字表示的角,并用三个大写字母表示.
(3)以D为顶点的角.
【思路点拨】(1)以某点为顶点的角只有一个时才能用一个大写字母表示.
(2)找出标有数字的角,并用三个大写字母表示.
(3)找以D为端点的射线(或线段)形成的角,并用三个字母表示.
【自主解答】(1)顶点处只有一个角的为∠B,所以能用一个大写字母表示的角为∠B.
(2)∠1用三个大写字母表示为∠CAD, ∠2用三个大写字母表示为∠ACE, ∠3用三个大写字母表示为∠ABD.
(3)∠ADC,∠ADB.
【总结提升】表示角时注意的三点
1.用三个字母表示角时,顶点字母必须写在中间.
2.用一个字母表示角时,必须顶点处只有一个角.
3.用数字或希腊字母表示角时,必须在相应角的内部加弧线及数字或希腊字母.
知识点 2 角的度、分、秒的换算
【例2】(1)把4.62°化成度、分、秒.
(2)把45°23′45″化成度.
【教你解题】
【总结提升】度、分、秒相互换算的法则
1.度、分、秒的换算是60进制.
2.角的度数的换算有两种情况:
(1)把度化成度、分、秒的形式,即从高单位向低单位转化时,每级变化乘以60.
(2)把度、分、秒化成度的形式,即从低单位向高单位转化时,每级变化除以60.
题组一:角的识别与表示
1.下列关于角的说法正确的是( )
A.两条射线组成的图形叫做角
B.延长一个角的两边
C.角的两边是射线,所以角不可以度量
D.角的大小与这个角的两边长短无关
【解析】选D.形成角的两条射线应有公共端点,A不正确;角的边是射线不能延长,B不正确;角的大小是指两边张开的幅度,可以度量,与边的长短无关,C不正确.
2.下图中表示∠ABC的图是( )
【解析】选C.选项A为∠CAB,选项B不是角;选项D为∠ACD.
3.如图所示,下列表示角的方法中错
误的是( )
A.∠1与∠AOB表示同一个角
B.∠AOC也可以用∠O来表示
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠β表示的是∠BOC
【解析】选B.以O为顶点的角有三个,不能用一个大写字母来表示.
4.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
【解析】选D.前三个选项以O为顶点的角都不止一个,所以都不能用一个大写字母来表示 .
5.写出如图所示的符合下列条件的角(图中
所有的角指小于平角的角).
(1)能用一个大写字母表示的角.
(2)以A为顶点的角.
(3)图中所有的角(可用简便方法表示).
【解析】(1)∠B,∠C.
(2)∠1或∠CAD,∠2或∠DAB,∠CAB.
(3)∠C,∠1,∠2,∠CAB,∠B,∠3,∠4.
题组二:角的度、分、秒的换算
1.14时的钟表的时针与分针所形成的角的度数是( )
A.30° B.45°
C.60° D.90°
【解析】选C.钟表的1个大格是 周角=30°,14时的时针与
分针形成的角是2个大格,故为60°.
2.(1)3.76°=________度________分________秒.
(2)3.76°=________分=________秒.
【解析】(1)0. 76°=0.76×60=45.6′,0.6′=0.6×60=36″,所以3.76°=3°45′36″.(2) 3.76°=3.76×60=225.6′,225.6′=225.6×60=13 536″.
答案:(1)3 45 36
(2)225.6 13 536
3.把35°24′36″化成用度表示的形式.
【解析】因为36″=36÷60=0.6′,所以24′36″=24.6′=
24.6÷60=0.41°,所以35°24′36″=35.41°.
4.32°18′与32.18°哪个大?
【解析】方法一:因为32°18′=32.3°,32.3°>32.18°,
所以32°18′>32.18°.
方法二:因为0. 18°=10.8′,所以32.18°=32°10.8′,又因为32°18′>32°10.8′,所以32°18′>32.18°.
5.如图,分别确定四个城市相应钟表上时针与分针所成角的度数(小于平角的角).
【解析】巴黎:30°,伦敦:0°,北京:30°×4=120°,东京:30°×3=90°.
【想一想错在哪?】钟表上3时30分的时针与分针的夹角是多少?
提示:要弄清时针、分针特别是时针所在的位置.
