人教版九年级数学 第二十八章过关训练课件(共35张PPT)
文档属性
| 名称 | 人教版九年级数学 第二十八章过关训练课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 14:07:30 | ||
图片预览











文档简介
(共35张PPT)
第二十八章过关训练
B
2. 在Rt△ABC中,各边都扩大为原来的5倍,则∠A的正弦函数值( )
A. 不变 B. 扩大为原来的5倍
C. 缩小为原来的5倍 D. 不能确定
A
3. 如图S28-1,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
D
4. 在Rt△ABC中,∠C=90°,AC=3,AB=5,则cos A的值为( )
B
A
D
B
8. 如图S28-2,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于点D,设∠ACD=α,则cos α的值为( )
A
B
B
二、填空题(本大题5小题,每小题3分,共15分)
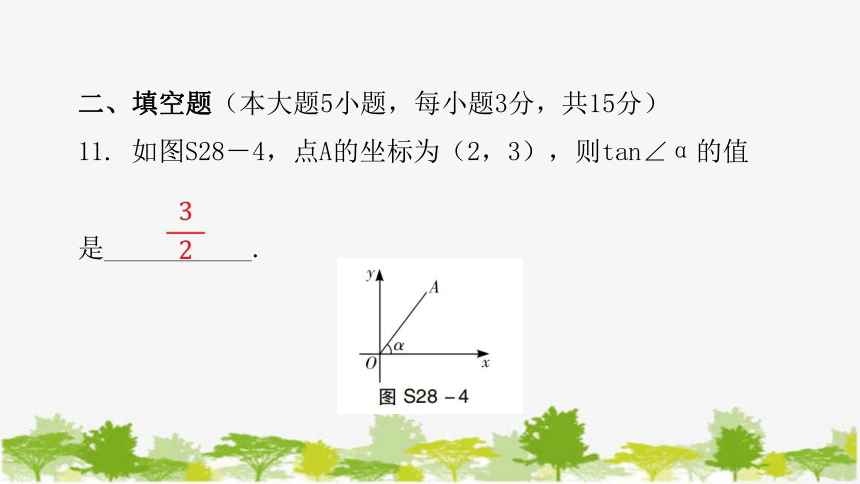
11. 如图S28-4,点A的坐标为(2,3),则tan∠α的值
是___________.
12. 如图S28-5,在离地面高度为5 m的A处引拉线固定电线杆,若要使拉线与地面的夹角α=37°,则工作人员需买拉线的长度约为_________m.(结果精确到1 m,sin 37°≈
0.6,cos 37°≈0.8)
8
13. 如图S28-6,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为
____________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16. 计算:2sin 60°tan 45°+4cos2 30°-tan 60°.
20. 如图S28-12,为了测得一棵树的高度AB,小明在D处用高为1 m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10 m,又测得树顶A的仰角为60°,求这棵树的高度AB.
21. 如图S28-13,水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1∶0.6,背水坡坡比为1∶2,大坝高DE为30 m,坝顶宽CD为10 m,求大坝的截面的周长和面积.
22.如图S28-14,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100 n mile的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.
(1)求B处与灯塔P之间的距离;(结果精确到0.1 n mile)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150 n mile的点O处.圆形暗礁区域的半径为60 n mile,进入这个区域,就有触礁的危险.
五、解答题(三)(本大题2小题,每小题12分,共24分)
23. 为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,如图S28-15,他们在河南岸的点A处测得河北岸的树H恰好在点A的正北方向. 测量方案与数据如下表:
课题 测量河流宽度
测量工具 测量角度的仪器、皮尺等
测量小组 第一小组 第二小组 第三小组
测量方案 示意图
说明 点B,C在点A的正东方向 点B,D在点A的正东方向 点B在点A的正东方向,
点C在点A的正西方向
测量数据 BC=60 m, ∠ABH=70°, ∠ACH=35° BD=20 m, ∠ABH=70°, ∠BCD=35° BC=101 m,
∠ABH=70°,
∠ACH=35°
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个小组的方案及其数据求出河宽(结果精确到0.1 m,参考数据:sin 70°≈0.94,sin 35°≈0.57,tan 70°≈2.75,tan 35°≈0.70)
解:(1)第二小组的数据无法计算出河宽.
谢 谢
第二十八章过关训练
B
2. 在Rt△ABC中,各边都扩大为原来的5倍,则∠A的正弦函数值( )
A. 不变 B. 扩大为原来的5倍
C. 缩小为原来的5倍 D. 不能确定
A
3. 如图S28-1,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
D
4. 在Rt△ABC中,∠C=90°,AC=3,AB=5,则cos A的值为( )
B
A
D
B
8. 如图S28-2,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于点D,设∠ACD=α,则cos α的值为( )
A
B
B
二、填空题(本大题5小题,每小题3分,共15分)
11. 如图S28-4,点A的坐标为(2,3),则tan∠α的值
是___________.
12. 如图S28-5,在离地面高度为5 m的A处引拉线固定电线杆,若要使拉线与地面的夹角α=37°,则工作人员需买拉线的长度约为_________m.(结果精确到1 m,sin 37°≈
0.6,cos 37°≈0.8)
8
13. 如图S28-6,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为
____________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16. 计算:2sin 60°tan 45°+4cos2 30°-tan 60°.
20. 如图S28-12,为了测得一棵树的高度AB,小明在D处用高为1 m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10 m,又测得树顶A的仰角为60°,求这棵树的高度AB.
21. 如图S28-13,水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1∶0.6,背水坡坡比为1∶2,大坝高DE为30 m,坝顶宽CD为10 m,求大坝的截面的周长和面积.
22.如图S28-14,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100 n mile的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.
(1)求B处与灯塔P之间的距离;(结果精确到0.1 n mile)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150 n mile的点O处.圆形暗礁区域的半径为60 n mile,进入这个区域,就有触礁的危险.
五、解答题(三)(本大题2小题,每小题12分,共24分)
23. 为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,如图S28-15,他们在河南岸的点A处测得河北岸的树H恰好在点A的正北方向. 测量方案与数据如下表:
课题 测量河流宽度
测量工具 测量角度的仪器、皮尺等
测量小组 第一小组 第二小组 第三小组
测量方案 示意图
说明 点B,C在点A的正东方向 点B,D在点A的正东方向 点B在点A的正东方向,
点C在点A的正西方向
测量数据 BC=60 m, ∠ABH=70°, ∠ACH=35° BD=20 m, ∠ABH=70°, ∠BCD=35° BC=101 m,
∠ABH=70°,
∠ACH=35°
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个小组的方案及其数据求出河宽(结果精确到0.1 m,参考数据:sin 70°≈0.94,sin 35°≈0.57,tan 70°≈2.75,tan 35°≈0.70)
解:(1)第二小组的数据无法计算出河宽.
谢 谢
