16.3.1 分式方程[下学期]
文档属性
| 名称 | 16.3.1 分式方程[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 607.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-26 15:54:00 | ||
图片预览






文档简介
课件17张PPT。 1、一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间, 与以最大航速航行60千米所用时间相等, 则江水的流速为多少?
【想一想 做一做】2、某地电话公司调低了长途电话的话费标准,每分钟通话费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟,问前后两种收费标准分别为多少? 1、2(x-1)=x+1; ; x+2y=1…2、 整式方程:方程两边都是整式的方程.(即分母中不含未知数的方程)分式方程:分母中含有未知数的方程观察下列方程: 请识分式方程真面目 下列方程中,哪些是分式方程?辨别是非 为什么要去分母?
去分母前后的方程有什么区别?分式方程整式方程去分母尝试解分式方程:探索解分式方程的思路:转化思想 解:去分母,方程两边都乘以6得,3(2x-1)-6=2x+3去括号,得6x-3-6=2x+3移项,得6x-2x=3+3+6合并同类项,得4x=12系数化为1,得x=3 解一元一次方程的一般步骤是什么?你会解整式方程吗例1 解分式方程
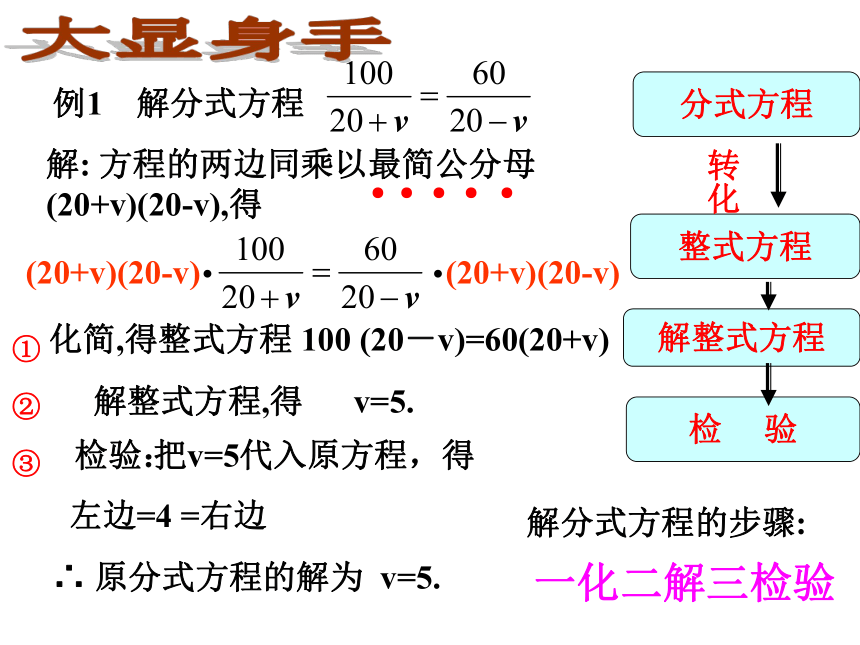
化简,得整式方程 100 (20-v)=60(20+v)解整式方程,得 v=5. 把v=5代入原方程,得
左边=4 =右边∴ 原分式方程的解为 v=5.● ● ● ● ●分式方程整式方程解整式方程检 验转化① ② ③检验:(20+v)(20-v)(20+v)(20-v)..一化二解三检验解分式方程的步骤:大显身手例2 解分式方程 解 方程两边同乘以最简公分母(x+1)(x-1),解整式方程,得 x1=-1, x2=8 得 (x-1)2 =5x+9x2-2x+1=5x+9
X2-7x-8=0
(x+1)(x-8)=0解分式方程的基本思路:
例2 解分式方程 解 方程两边同乘以最简公分母(x+1)(x-1),解整式方程,得 x1=-1, x2=8检验:把x1=-1,x2=8分别代入原方程当x1=-1时, 原方程的两个分母值为零,分式无意义,因此x1=-1不是原方程的根.当x2=8时, 左边= , 右边=
左边=右边, 因此x2=8是原方程的根.∴ 原分式方程的根是x=8.① ② ③ 得 (x-1)2 =5x+9例2 解分式方程 解 方程两边同乘以最简公分母(x+1)(x-1),解整式方程,得 x = -1 检验:把x = -1 代入原方程结果使原方程的最简公分母x2-1=0 ,分式无意义,因此x = -1不是原方程的根. ∴ 原方程无解 .① ② ③ 得 (x-1)2 =5x+9+1+1·(x+1)(x-1)增根x2-2x+1=5x+9+x2-1
-7x=7
x=-1增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.即:使分母值为零的根···· · · ···1、如果 有增根,那么增根为 .X=22、如果方程 有增根,那么
增根为________。=X=0或x=2增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.增根产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.········即:使分母值为零的根···· · · ···(填空) 1、解方程:
x(x-2)x 2+ x -6=0-3 2
-3(-3-2) 15
2(2-2) 2-3练 一 练·· ·······① 化简得 . 解得 x1= , x2= .
检验:把x1= ,代入最简公分母,
x(x-2)= = ≠0;
把x2= ,代入最简公分母,
x(x-2)= =0
∴x= 是增根,舍去.
∴原方程的根是x= .
-32解:方程两边同乘以 ,②③当m为何值时,去分母解方程:
会产生增根?反思:分式方程产生增根,也就是使分母等于0.
将原分式方程去分母后,代入增根.没有解.议一议,启迪思维1、通过这节课的学习,你学到了
哪些数学知识?数学方法?
2、你还有什么新的发现?
3、你还有什么困惑?
学后思: 解分式方程一般需要哪几个步骤?
去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
结论 :确定分式方程的解.这里的检验要以计算正确为前提一 化
二 解
三检验
学习是件很愉快的事,但又是一件很困难的事.困难是虎又是羊,看你是虎还是羊.你是绵羊它是虎, 你是老虎它是羊.再见!
【想一想 做一做】2、某地电话公司调低了长途电话的话费标准,每分钟通话费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟,问前后两种收费标准分别为多少? 1、2(x-1)=x+1; ; x+2y=1…2、 整式方程:方程两边都是整式的方程.(即分母中不含未知数的方程)分式方程:分母中含有未知数的方程观察下列方程: 请识分式方程真面目 下列方程中,哪些是分式方程?辨别是非 为什么要去分母?
去分母前后的方程有什么区别?分式方程整式方程去分母尝试解分式方程:探索解分式方程的思路:转化思想 解:去分母,方程两边都乘以6得,3(2x-1)-6=2x+3去括号,得6x-3-6=2x+3移项,得6x-2x=3+3+6合并同类项,得4x=12系数化为1,得x=3 解一元一次方程的一般步骤是什么?你会解整式方程吗例1 解分式方程
化简,得整式方程 100 (20-v)=60(20+v)解整式方程,得 v=5. 把v=5代入原方程,得
左边=4 =右边∴ 原分式方程的解为 v=5.● ● ● ● ●分式方程整式方程解整式方程检 验转化① ② ③检验:(20+v)(20-v)(20+v)(20-v)..一化二解三检验解分式方程的步骤:大显身手例2 解分式方程 解 方程两边同乘以最简公分母(x+1)(x-1),解整式方程,得 x1=-1, x2=8 得 (x-1)2 =5x+9x2-2x+1=5x+9
X2-7x-8=0
(x+1)(x-8)=0解分式方程的基本思路:
例2 解分式方程 解 方程两边同乘以最简公分母(x+1)(x-1),解整式方程,得 x1=-1, x2=8检验:把x1=-1,x2=8分别代入原方程当x1=-1时, 原方程的两个分母值为零,分式无意义,因此x1=-1不是原方程的根.当x2=8时, 左边= , 右边=
左边=右边, 因此x2=8是原方程的根.∴ 原分式方程的根是x=8.① ② ③ 得 (x-1)2 =5x+9例2 解分式方程 解 方程两边同乘以最简公分母(x+1)(x-1),解整式方程,得 x = -1 检验:把x = -1 代入原方程结果使原方程的最简公分母x2-1=0 ,分式无意义,因此x = -1不是原方程的根. ∴ 原方程无解 .① ② ③ 得 (x-1)2 =5x+9+1+1·(x+1)(x-1)增根x2-2x+1=5x+9+x2-1
-7x=7
x=-1增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.即:使分母值为零的根···· · · ···1、如果 有增根,那么增根为 .X=22、如果方程 有增根,那么
增根为________。=X=0或x=2增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.增根产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.········即:使分母值为零的根···· · · ···(填空) 1、解方程:
x(x-2)x 2+ x -6=0-3 2
-3(-3-2) 15
2(2-2) 2-3练 一 练·· ·······① 化简得 . 解得 x1= , x2= .
检验:把x1= ,代入最简公分母,
x(x-2)= = ≠0;
把x2= ,代入最简公分母,
x(x-2)= =0
∴x= 是增根,舍去.
∴原方程的根是x= .
-32解:方程两边同乘以 ,②③当m为何值时,去分母解方程:
会产生增根?反思:分式方程产生增根,也就是使分母等于0.
将原分式方程去分母后,代入增根.没有解.议一议,启迪思维1、通过这节课的学习,你学到了
哪些数学知识?数学方法?
2、你还有什么新的发现?
3、你还有什么困惑?
学后思: 解分式方程一般需要哪几个步骤?
去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
结论 :确定分式方程的解.这里的检验要以计算正确为前提一 化
二 解
三检验
学习是件很愉快的事,但又是一件很困难的事.困难是虎又是羊,看你是虎还是羊.你是绵羊它是虎, 你是老虎它是羊.再见!
