轴对称与坐标变化课件

课件23张PPT。
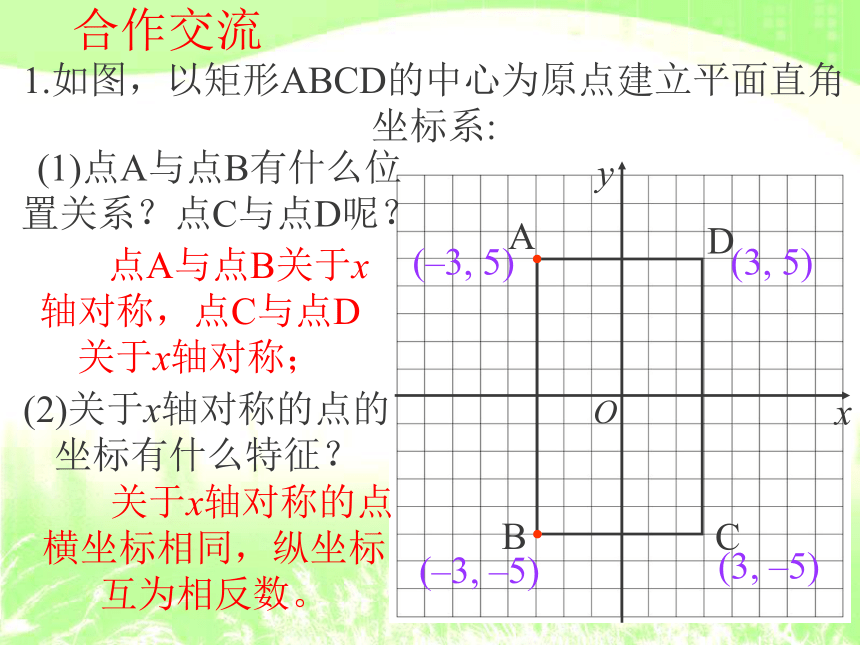
轴对称与坐标变化合作交流1.如图，以矩形ABCD的中心为原点建立平面直角坐标系:DABC(–3, 5)(–3, –5)(3, –5)(3, 5)(1)点A与点B有什么位
置关系？点C与点D呢？ 点A与点B关于x
轴对称，点C与点D
关于x轴对称；(2)关于x轴对称的点的
坐标有什么特征？ 关于x轴对称的点
横坐标相同，纵坐标
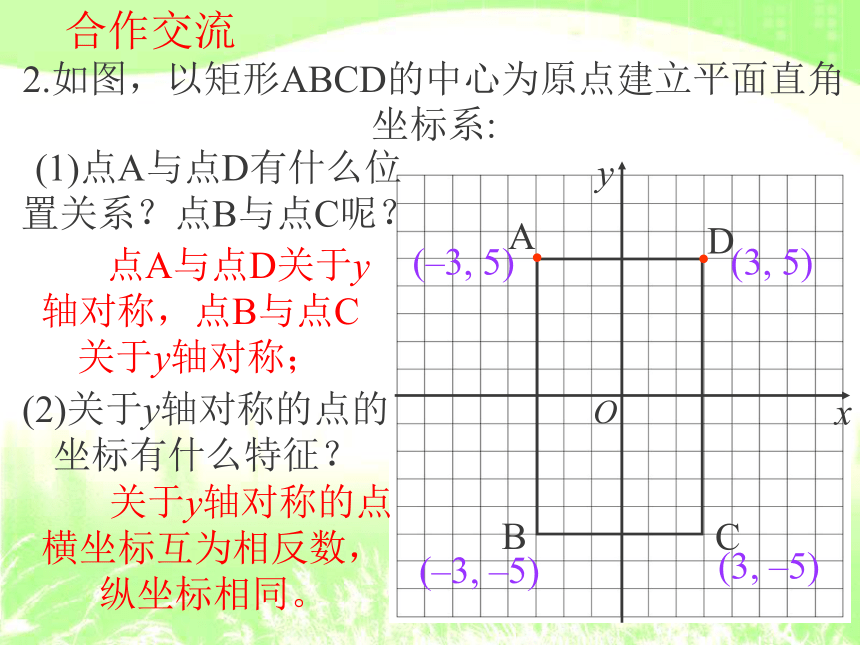
互为相反数。新知归纳“关于坐标轴对称的点”的坐标特征：(1) 关于x轴对称的点的坐标：横同纵反；合作交流2.如图，以矩形ABCD的中心为原点建立平面直角坐标系:DABC(–3, 5)(–3, –5)(3, –5)(3, 5)(1)点A与点D有什么位
置关系？点B与点C呢？ 点A与点D关于y
轴对称，点B与点C
关于y轴对称；(2)关于y轴对称的点的
坐标有什么特征？ 关于y轴对称的点
横坐标互为相反数，
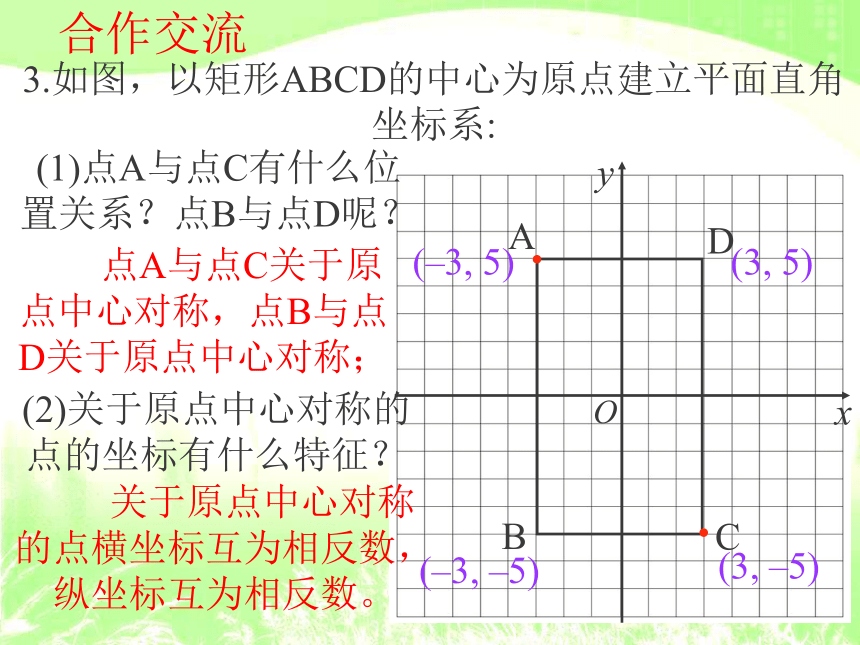
纵坐标相同。新知归纳“关于坐标轴对称的点”的坐标特征：(1) 关于x轴对称的点的坐标：横同纵反；(2) 关于y轴对称的点的坐标：横反纵同。合作交流3.如图，以矩形ABCD的中心为原点建立平面直角坐标系:DABC(–3, 5)(–3, –5)(3, –5)(3, 5)(1)点A与点C有什么位
置关系？点B与点D呢？ 点A与点C关于原
点中心对称，点B与点
D关于原点中心对称；(2)关于原点中心对称的
点的坐标有什么特征？ 关于原点中心对称
的点横坐标互为相反数，
纵坐标互为相反数。新知归纳“关于原点对称的点”的坐标特征：关于原点中心对称的点的坐标：横纵皆反。3、“关于坐标轴对称的点”的坐标特征：(1) 关于x轴对称的点的坐标：横同纵反；(2) 关于y轴对称的点的坐标：横反纵同。4、“关于原点对称的点”的坐标特征：关于原点中心对称的点的坐标：横纵皆反。归纳：关于y轴对称的点的坐标的特点是:横坐标互为相反数,纵坐标相等.练习:
1、点P(-5, 6)与点Q关于y轴对称，则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于y轴对称，则a=_____, b =_____.( 5 , 6 )2-5（简称：纵轴纵相等）小结：在平面直角坐标系中，关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点（x, y）关于x轴对称的点的坐标为______.
点（x, y）关于y轴对称的点的坐标为______.(x, － y)(－ x, y)1、完成下表.
(-2, -3)(2,3)(-1,-2)(1, 2)(6, -5)(-6, 5)(0, -1.6)(0,1.6)(-4,0)(4,0)练习2.将一个点的纵坐标不变，横坐标乘以－1，得到的点与原来的点的位置关系是 ；将一个点的横坐标不变，纵坐标乘以－1，得到的点与原来的点的位置关系是 ____ _ 关于y轴对称关于x轴对称3、分别写出下列各点关于x轴和y轴对称的点的坐标．
（３，６） （－７，９） （６，－１）
（－３．－５） 　（０，１０）
4、根据下列点的坐标的变化，判断它们进
行了怎样的变换：
⑴　（－１，３）　　　（－１，－３）
⑵　（－５，－４）　　（－５，４）
⑶　（３，４）　　　　（－３，４）
⑷　（１，０）　　　　（－１，０）4、已知点A（m+2，3）、B（-5，n+6）关于y轴对称，则m= ，n=____
(1)Q,P两点关于x轴对称； 5、已知点Q(m,3),P(-5,n),根据以下要求确定m,n的值(2)Q,P两点关于y轴对称；(3)PQ∥x轴；(4)PQ∥y轴；-336、已知点A(2m+1，m-3)关于y轴的对称点在第四象限，则m的取值范围是 。例：已知△ABC的三个顶点的坐标分别为A(-3，5),B(- 4，1),C(-1，3)，作出△ABC关于y轴和x轴对称的图形。····AB ′A ′C ′2、将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形( A )
　　A 关于X轴对称. B 关于Y轴对称
　　C 关于原点对称 D 无法确定
3、点A(-3,2)与点B(-3,-2)的关系是（　　　　）
　Ａ关于Ｘ轴对称　　　Ｂ关于Ｙ轴对称
　Ｃ关于原点对称　　　Ｄ以上各项都不对
４已知点Ｍ(3,-2),点N(a,b)是Ｍ点关于Ｙ轴的对称点， 则 a= b=
5、已知点Ｐ(a-1,5)和点Ｑ(2,b-1)关于Ｘ轴对称，则
　 a= b=
A-3-23-42.如图，从图形I到图形II是进行了平移还是轴对称？如果是轴对称，找出对称轴；如果是平移，是怎样的平移？① 图形I到图形II是进行了轴对称变换，对称轴是x轴； 练习:
1、点P(-5, 6)与点Q关于x轴对称，则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于x轴对称，则a=_____, b =_____.
3、点P(-5, 6)与点Q关于y轴对称，则点Q的坐标为__________.
4、点M(a, -5)与点N(-2, b)关于y轴对称，则a=_____, b =_____.
5、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称，则a=_____ b=_______.
若点p与点p’关于y轴对称，则a=_____ b=_______.A`（-４,-1）如图，利用关于坐标轴对称的点的坐标的特点，分别作出△ABC关于X轴和y 轴对称的图形。···C`（-3,-2）B`（-1,1）6、在平面直角坐标系中，写出所有与△ABC全等的△FED中，F点的坐标＿。
A(-2,3)F(2,3)(2,3)xy A(-2,3)F(2,-3)(2,3)(2,3)
或(2,-3)xy 6、在平面直角坐标系中，写出所有与△ABC全等的△FED中，F点的坐标＿。
A(-2,3)F(3,3)(2,3)或(2,-3)或(3,3)xy 6、在平面直角坐标系中，写出所有与△ABC全等的△FED中，F点的坐标＿。
A(-2,3)F(3,-3)(3,3)(2,3)或(2,-3) 或(3,3)或(3,-3)xy 6、在平面直角坐标系中，写出所有与△ABC全等的△FED中，F点的坐标＿。