人教B版(2019)必修第一册《3.3 函数的应用(一)》2022年同步练习卷(含答案)
文档属性
| 名称 | 人教B版(2019)必修第一册《3.3 函数的应用(一)》2022年同步练习卷(含答案) | 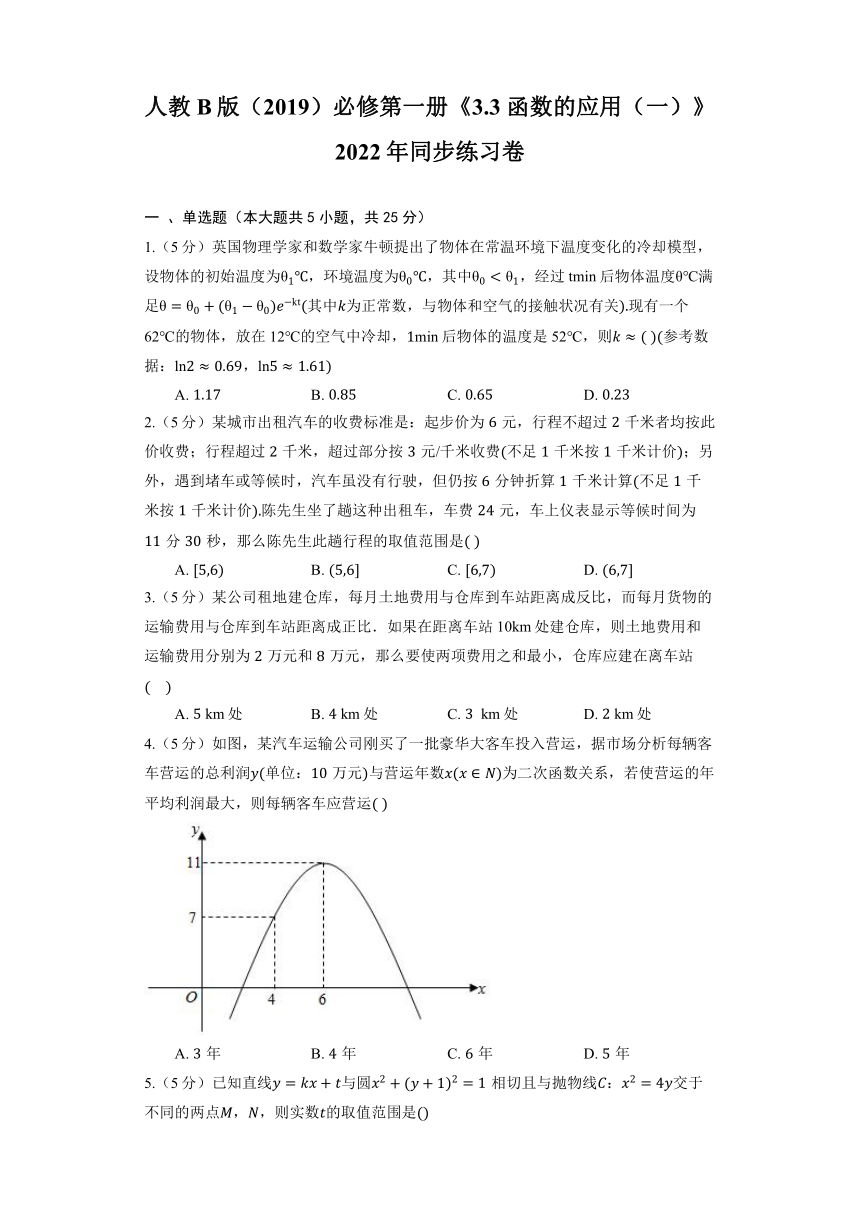 | |
| 格式 | docx | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 16:16:58 | ||
图片预览




文档简介
人教B版(2019)必修第一册《3.3 函数的应用(一)》2022年同步练习卷
一 、单选题(本大题共5小题,共25分)
1.(5分)英国物理学家和数学家牛顿提出了物体在常温环境下温度变化的冷却模型,设物体的初始温度为,环境温度为,其中,经过后物体温度满足其中为正常数,与物体和空气的接触状况有关现有一个的物体,放在的空气中冷却,后物体的温度是,则参考数据:,
A. B. C. D.
2.(5分)某城市出租汽车的收费标准是:起步价为元,行程不超过千米者均按此价收费;行程超过千米,超过部分按元千米收费不足千米按千米计价;另外,遇到堵车或等候时,汽车虽没有行驶,但仍按分钟折算千米计算不足千米按千米计价陈先生坐了趟这种出租车,车费元,车上仪表显示等候时间为分秒,那么陈先生此趟行程的取值范围是
A. B. C. D.
3.(5分)某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站处建仓库,则土地费用和运输费用分别为万元和万元,那么要使两项费用之和最小,仓库应建在离车站
A. 处 B. 处 C. 处 D. 处
4.(5分)如图,某汽车运输公司刚买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润单位:万元与营运年数为二次函数关系,若使营运的年平均利润最大,则每辆客车应营运
A. 年 B. 年 C. 年 D. 年
5.(5分)已知直线与圆相切且与抛物线:交于不同的两点,,则实数的取值范围是
A. B.
C. D.
二 、填空题(本大题共3小题,共15分)
6.(5分)如图,在平面直角坐标系中,平行于轴,四边形是边长为的正方形,记四边形位于直线左侧图形的面积为,则的大致图象是________.
7.(5分)长为,宽为的矩形,当长增加,且宽减少时面积最大,此时__________,最大面积__________.
8.(5分)某种圆柱形的饮料罐的容积为,为了使得它的制作用料最省即表面积最小,则饮料罐的底面半径为用含的代数式表示______
三 、解答题(本大题共4小题,共48分)
9.(12分)物体在常温下的温度单位:变化满足一定的规律:设物体的初始温度是,经过一定时间单位:后的温度是,则,其中表示环境温度,为正常数.现有一杯的热水放在的房间中,如果热水降温到需要,那么降温到时,需要多长时间.结果精确到,参考数据:,?
10.(12分)如城某观光区的平面示意图如图所示,其中矩形的长千米,宽千米,半圆的圆心为中点,为了便于游客观光休闲,在观光区铺设一条由圆弧、线段、组成的观光道路,其中线段经过圆心,且点在线段上不含线段端点,,已知道路,的造价为元每千米,道路造价为元每千米,设,观光道路的总造价为.
试求与的函数关系式:;
当为何值时,观光道路的总造价最小.
11.(12分)某水库堤坝因年久失修,发生了渗水现象,当发现时已有的坝面渗水,经测算知渗水现象正在以每天的速度扩散,当地政府积极组织工人进行抢修,已知每个工人平均每天可抢修渗水面积,每人每天所消耗的维修材料费元,劳务费元,另外给每人发放元的服装补贴,每渗水的损失为元.现在共派去名工人,抢修完成共用天.
写出关于的函数关系式;
要使总损失最小,应派多少名工人去抢修总损失渗水损失政府支出
12.(12分)为迎接冬奥会,石家庄准备进行城市绿化升级,在矩形街心广场中,如图,其中,,现将在其内部挖掘一个三角形空地进行盆景造型设计,其中点在边上,点在边上,要求
若,判断是否符合要求,并说明理由;
设,写出面积的关于的表达式,并求的最小值.
答案和解析
1.【答案】D;
【解析】解:由题意可知,,,
当时,,于是,
得,
,则,
故选:
将,,,代入公式,计算可知的值,
此题主要考查函数模型的选择与应用,考查指数方程的解法,考查运算求解能力,是中档题.
2.【答案】B;
【解析】解:设陈先生的行程为,
根据题意可得,陈先生要付的车费为,
,故实际行程应属于区间
故选:
设陈先生的行程为,根据题意列车费关于行程的关系式,求解即可.
此题主要考查分段函数在实际问题中的应用,解决本题的关键是要根据实际问题抽象出函数表达式,是基础题.
3.【答案】A;
【解析】解:设仓库与车站距离为,土地费用为,运输费用为,
于是,,
,解得,.
设总费用为,则.
当且仅当即时取等号.
故选:.
求出总费用与距离的函数解析式,利用基本不等式得出费用最小时对应的即可.
该题考查了函数模型的应用,函数最值的计算,属于中档题.
4.【答案】D;
【解析】解:设二次函数为,
将点代入,得,
故二次函数为,
则年平均利润为
当且仅当,即时,取等号,
每辆客车营运年,年平均利润最大,最大值为万元.
故选:
先根据图象求出二次函数解析式,欲使营运年平均利润最大,即求的最大值,故先表示出此式,再结合基本不等式即可求其最大值.
此题主要考查了二次函数的性质、基本不等式在最值问题中的应用、基本不等式等基础知识,考查运算求解能力、化归与转化思想,属于中档题
5.【答案】A;
【解析】解:因为直线:与圆:相切,
所以,
所以,
把直线方程代入抛物线方程并整理得:,
由得或,
实数的取值范围是为
故选:
由直线与圆相切可得,把直线方程代入抛物线方程并整理,由求得的范围.
此题主要考查直线和圆、抛物线的位置关系,考查化简整理的运算能力,属于中档题.
6.【答案】③;
【解析】
此题主要考查的知识点是函数图象的识别,熟练掌握分段函数解析式的求法及图象的画法是解答的关键.
解:当直线的与四边形的交点在,边上,即,直线左侧图形为三角形,
此时,此时函数的开口向上,为增函数,
当直线与四边形的交点在,上,即时,,
直线左侧图形为四边形,此时,函数的开口向下,函数为增函数,当直线的与四边形无交点,即时,函数的值成为定值,故只有③符合,
故答案为③.
7.【答案】
;
【解析】
此题主要考查函数的最值,根据题意可得,进而利用二次函数的性质即可求得结果
解:根据题目条件,即,
所以
故当时,取得最大值
故答案为,
8.【答案】;
【解析】解:设圆柱的底面半径,高,容积为,
则,即有,
用料为
,
当且仅当,即时最小即用料最省.
故答案为:.
设圆柱的底面半径,高容积为,则,,要求用料最省即圆柱的表面积最小,由题意可得,配凑基本不等式的形式,从而求最小值,从而可求高与底面半径之比,再由体积,即可得到所求.
这道题主要考查了基本不等式在最值求解中的应用,利用基本不等式的关键是要符合其形式,并且要注意验证等号成立的条件.
9.【答案】解:根据题干可以得到:.
代入对应公式可得:,解得h=10.
则得到.
可以解得t≈21.;
【解析】
由已知条件代入所给的式子可求出,再计算所求结果.
此题主要考查选择选择合适函数模型解决实际问题,属于中档题.
10.【答案】解:(1)由题意可知,过点F作FO⊥AB,垂足为O,则∠FPB=θ,
所以,.…(2)
…(4)
=()…(6)
(2)…(8)
即2coθ+7cosθ-4=0,或cosθ=-4(舍)…(10)
θ
y' - 0 +
y 最小
…(12)
所以时,y最小,即当时,观光道路的总造价最小.…(14);
【解析】
由题意可知,过点作,垂足为,则,求出,,即可求与的函数关系式:;
求导数,确定函数的单调性,即可得出当为何值时,观光道路的总造价最小.
此题主要考查三角函数知识,考查导数知识的运用,考查学生的计算能力,确定函数的解析式是关键.
11.【答案】解:(1)由题意知:抢修n天时,维修工人抢修的面积之和为4nx,而渗水的面积为400+4n,
所以有4nx=400+4n,可得(x≥2且x∈N+).
(2)设总损失为y,
则=,
当且仅当时,即x=21时,等号成立,
所以应派21名工人去抢修,总损失最小.;
【解析】
根据抢修的面积等于渗水的面积列出方程,求出且;
求出总损失关于的关系式,再利用基本不等式求出最小值,得到答案.
此题主要考查函数的实际应用,掌握基本不等式是解本题的关键,属于中档题.
12.【答案】解:(1)根据题意建立平面直角坐标系,如图所示:
则Q(100,0),P(400,200),D(0,300),
所以=(-400,100),=(-300,-200),
=120000-20000=100000,
||==100,||==100,
所以cos∠DPQ===≠,
所以∠DPQ≠,△DPQ不符合要求.
(2)解:因为∠CDP=θ且,可得,所以,
所以△DPQ的面积为:,
又因为=.
所以,即S的最小值平方米.;
【解析】
由,得到,,求得,,,在中,由余弦定理求得的值,即可求解.
因为,得到,进而得出的面积,结合三角函数的性质,即可求解.
此题主要考查函数的实际应用,考查学生的运算能力,属于中档题.
一 、单选题(本大题共5小题,共25分)
1.(5分)英国物理学家和数学家牛顿提出了物体在常温环境下温度变化的冷却模型,设物体的初始温度为,环境温度为,其中,经过后物体温度满足其中为正常数,与物体和空气的接触状况有关现有一个的物体,放在的空气中冷却,后物体的温度是,则参考数据:,
A. B. C. D.
2.(5分)某城市出租汽车的收费标准是:起步价为元,行程不超过千米者均按此价收费;行程超过千米,超过部分按元千米收费不足千米按千米计价;另外,遇到堵车或等候时,汽车虽没有行驶,但仍按分钟折算千米计算不足千米按千米计价陈先生坐了趟这种出租车,车费元,车上仪表显示等候时间为分秒,那么陈先生此趟行程的取值范围是
A. B. C. D.
3.(5分)某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站处建仓库,则土地费用和运输费用分别为万元和万元,那么要使两项费用之和最小,仓库应建在离车站
A. 处 B. 处 C. 处 D. 处
4.(5分)如图,某汽车运输公司刚买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润单位:万元与营运年数为二次函数关系,若使营运的年平均利润最大,则每辆客车应营运
A. 年 B. 年 C. 年 D. 年
5.(5分)已知直线与圆相切且与抛物线:交于不同的两点,,则实数的取值范围是
A. B.
C. D.
二 、填空题(本大题共3小题,共15分)
6.(5分)如图,在平面直角坐标系中,平行于轴,四边形是边长为的正方形,记四边形位于直线左侧图形的面积为,则的大致图象是________.
7.(5分)长为,宽为的矩形,当长增加,且宽减少时面积最大,此时__________,最大面积__________.
8.(5分)某种圆柱形的饮料罐的容积为,为了使得它的制作用料最省即表面积最小,则饮料罐的底面半径为用含的代数式表示______
三 、解答题(本大题共4小题,共48分)
9.(12分)物体在常温下的温度单位:变化满足一定的规律:设物体的初始温度是,经过一定时间单位:后的温度是,则,其中表示环境温度,为正常数.现有一杯的热水放在的房间中,如果热水降温到需要,那么降温到时,需要多长时间.结果精确到,参考数据:,?
10.(12分)如城某观光区的平面示意图如图所示,其中矩形的长千米,宽千米,半圆的圆心为中点,为了便于游客观光休闲,在观光区铺设一条由圆弧、线段、组成的观光道路,其中线段经过圆心,且点在线段上不含线段端点,,已知道路,的造价为元每千米,道路造价为元每千米,设,观光道路的总造价为.
试求与的函数关系式:;
当为何值时,观光道路的总造价最小.
11.(12分)某水库堤坝因年久失修,发生了渗水现象,当发现时已有的坝面渗水,经测算知渗水现象正在以每天的速度扩散,当地政府积极组织工人进行抢修,已知每个工人平均每天可抢修渗水面积,每人每天所消耗的维修材料费元,劳务费元,另外给每人发放元的服装补贴,每渗水的损失为元.现在共派去名工人,抢修完成共用天.
写出关于的函数关系式;
要使总损失最小,应派多少名工人去抢修总损失渗水损失政府支出
12.(12分)为迎接冬奥会,石家庄准备进行城市绿化升级,在矩形街心广场中,如图,其中,,现将在其内部挖掘一个三角形空地进行盆景造型设计,其中点在边上,点在边上,要求
若,判断是否符合要求,并说明理由;
设,写出面积的关于的表达式,并求的最小值.
答案和解析
1.【答案】D;
【解析】解:由题意可知,,,
当时,,于是,
得,
,则,
故选:
将,,,代入公式,计算可知的值,
此题主要考查函数模型的选择与应用,考查指数方程的解法,考查运算求解能力,是中档题.
2.【答案】B;
【解析】解:设陈先生的行程为,
根据题意可得,陈先生要付的车费为,
,故实际行程应属于区间
故选:
设陈先生的行程为,根据题意列车费关于行程的关系式,求解即可.
此题主要考查分段函数在实际问题中的应用,解决本题的关键是要根据实际问题抽象出函数表达式,是基础题.
3.【答案】A;
【解析】解:设仓库与车站距离为,土地费用为,运输费用为,
于是,,
,解得,.
设总费用为,则.
当且仅当即时取等号.
故选:.
求出总费用与距离的函数解析式,利用基本不等式得出费用最小时对应的即可.
该题考查了函数模型的应用,函数最值的计算,属于中档题.
4.【答案】D;
【解析】解:设二次函数为,
将点代入,得,
故二次函数为,
则年平均利润为
当且仅当,即时,取等号,
每辆客车营运年,年平均利润最大,最大值为万元.
故选:
先根据图象求出二次函数解析式,欲使营运年平均利润最大,即求的最大值,故先表示出此式,再结合基本不等式即可求其最大值.
此题主要考查了二次函数的性质、基本不等式在最值问题中的应用、基本不等式等基础知识,考查运算求解能力、化归与转化思想,属于中档题
5.【答案】A;
【解析】解:因为直线:与圆:相切,
所以,
所以,
把直线方程代入抛物线方程并整理得:,
由得或,
实数的取值范围是为
故选:
由直线与圆相切可得,把直线方程代入抛物线方程并整理,由求得的范围.
此题主要考查直线和圆、抛物线的位置关系,考查化简整理的运算能力,属于中档题.
6.【答案】③;
【解析】
此题主要考查的知识点是函数图象的识别,熟练掌握分段函数解析式的求法及图象的画法是解答的关键.
解:当直线的与四边形的交点在,边上,即,直线左侧图形为三角形,
此时,此时函数的开口向上,为增函数,
当直线与四边形的交点在,上,即时,,
直线左侧图形为四边形,此时,函数的开口向下,函数为增函数,当直线的与四边形无交点,即时,函数的值成为定值,故只有③符合,
故答案为③.
7.【答案】
;
【解析】
此题主要考查函数的最值,根据题意可得,进而利用二次函数的性质即可求得结果
解:根据题目条件,即,
所以
故当时,取得最大值
故答案为,
8.【答案】;
【解析】解:设圆柱的底面半径,高,容积为,
则,即有,
用料为
,
当且仅当,即时最小即用料最省.
故答案为:.
设圆柱的底面半径,高容积为,则,,要求用料最省即圆柱的表面积最小,由题意可得,配凑基本不等式的形式,从而求最小值,从而可求高与底面半径之比,再由体积,即可得到所求.
这道题主要考查了基本不等式在最值求解中的应用,利用基本不等式的关键是要符合其形式,并且要注意验证等号成立的条件.
9.【答案】解:根据题干可以得到:.
代入对应公式可得:,解得h=10.
则得到.
可以解得t≈21.;
【解析】
由已知条件代入所给的式子可求出,再计算所求结果.
此题主要考查选择选择合适函数模型解决实际问题,属于中档题.
10.【答案】解:(1)由题意可知,过点F作FO⊥AB,垂足为O,则∠FPB=θ,
所以,.…(2)
…(4)
=()…(6)
(2)…(8)
即2coθ+7cosθ-4=0,或cosθ=-4(舍)…(10)
θ
y' - 0 +
y 最小
…(12)
所以时,y最小,即当时,观光道路的总造价最小.…(14);
【解析】
由题意可知,过点作,垂足为,则,求出,,即可求与的函数关系式:;
求导数,确定函数的单调性,即可得出当为何值时,观光道路的总造价最小.
此题主要考查三角函数知识,考查导数知识的运用,考查学生的计算能力,确定函数的解析式是关键.
11.【答案】解:(1)由题意知:抢修n天时,维修工人抢修的面积之和为4nx,而渗水的面积为400+4n,
所以有4nx=400+4n,可得(x≥2且x∈N+).
(2)设总损失为y,
则=,
当且仅当时,即x=21时,等号成立,
所以应派21名工人去抢修,总损失最小.;
【解析】
根据抢修的面积等于渗水的面积列出方程,求出且;
求出总损失关于的关系式,再利用基本不等式求出最小值,得到答案.
此题主要考查函数的实际应用,掌握基本不等式是解本题的关键,属于中档题.
12.【答案】解:(1)根据题意建立平面直角坐标系,如图所示:
则Q(100,0),P(400,200),D(0,300),
所以=(-400,100),=(-300,-200),
=120000-20000=100000,
||==100,||==100,
所以cos∠DPQ===≠,
所以∠DPQ≠,△DPQ不符合要求.
(2)解:因为∠CDP=θ且,可得,所以,
所以△DPQ的面积为:,
又因为=.
所以,即S的最小值平方米.;
【解析】
由,得到,,求得,,,在中,由余弦定理求得的值,即可求解.
因为,得到,进而得出的面积,结合三角函数的性质,即可求解.
此题主要考查函数的实际应用,考查学生的运算能力,属于中档题.
