16.1.1从分数到分式[下学期]
文档属性
| 名称 | 16.1.1从分数到分式[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-10 00:00:00 | ||
图片预览








文档简介
课件26张PPT。16.1分式1、下列两个整数相除如何表示成分数的形式:
3÷4= , 10 ÷ 3= ,
12 ÷11= , -7 ÷2= .
2、在代数式中,整式的除法也可以类似地表示。
试用类似分数的形式表示下列整式的除法:
⑴ 90÷x 可以用式子 来表示。
60÷(x-6)可以用式子 来表示。
(2) n公顷麦田共收小麦m吨,
平均每公顷产量可以用式子 吨来表示. 知识回顾像10a+2b、 、 、2a2这样含有
字母的数学表达式称为代数式.
整式单项式:数与字母或字母与字母的积多项式:几个单项式的和注意:代数式包括整式,也就是说整式是代数式但代数
式就不一定是整式了.有了这些预备知识,这节课我们将要学习另外一种
代数式! 一起努力!16.1.1从分数到分式 为了调查珍稀动物资源,动物专家在p平方米的保护区内找到7只灰熊,那么该保护区
每平方米有____只灰熊.
解:根据题意可知,
该保护区每平方米内灰熊的只数是:7÷p=
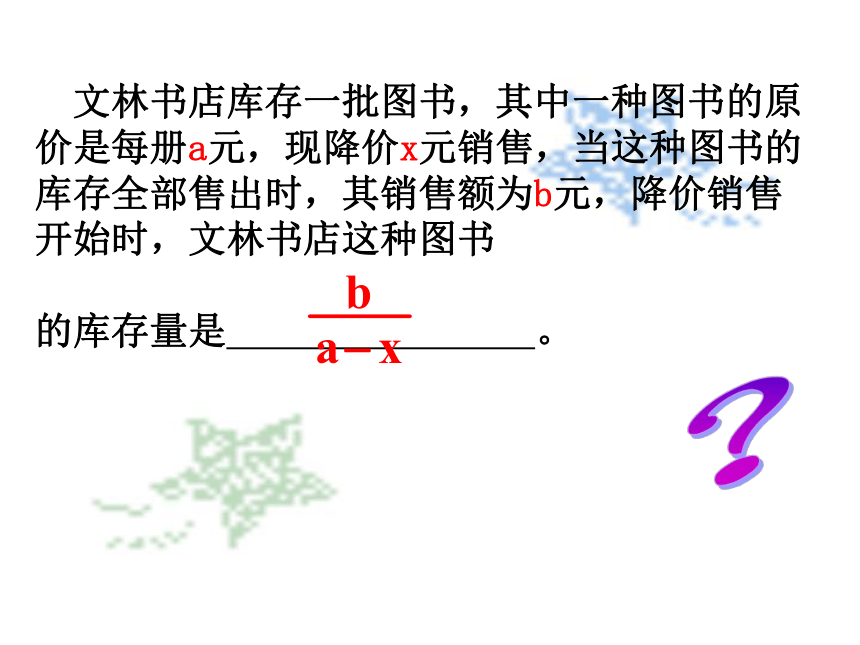
? 文林书店库存一批图书,其中一种图书的原价是每册a元,现降价x元销售,当这种图书的库存全部售出时,其销售额为b元,降价销售开始时,文林书店这种图书
的库存量是 。
甲种糖果每千克价格a元,乙种糖果价格b元,取甲种糖果m㎏,乙种糖果n㎏,混合后,平均
每千克价格 元。 轮船在静水中每小时走a千米,水流速度为每小时b千米,轮船在逆流中航行s千米,然后又返回出发地,那么轮船需要的
时间是 小时。 一件商品售价x元,利润率为a%
(a>0),则这种商品每件的成
本是 元。议一议上面题中出现了代数式 它们有什么共同特征?它们与整式有什么不同? 这些代数式都
表示两个整式相除,并且除式中含有字母.像这样的代数式就叫做分式 注解:
(1)分式也是代数式;
(2)分式是两个整式的商,它的形式是 (其中A,B都是
整式并且还要求B是含有字母的整式)
(3)A称为分式的分子,B为分式的分母。 注意:分式中字母的取值不能使分母为零.因为当分母的值为零时,分式就没有意义.关于分式的几点说明分数线有除号和括号的作用,如:分式是两个整式相除的商式。
对于任意一个分式,分母都不为零。1 2你真的清楚了吗?下列各式中,谁是整式?谁是分式?分式整
式想一想下列各式中,哪些是整式?哪些是分式?5x-7, 3x2-1, -5,试着自己举出分式的例子
练一练 课本:1,2(1)当a=1,2时,分别求分式 的值。做一做(2)当a取何值时,分式 无意义?(4)当a取何值时,分式 值为零?
(3)当a取何值时,分式 有意义? 例1 对于分式
(1)当x取什么数时,分式有意义?(2)当x取什么数时,分式的值是零?(3)当x=1时,分式的值是多少?例1 当x取什么值时,下列分式有意义?⑴ , ⑵ , ⑶解⑴:由分母 x-2=0,得 x=2。所以当 x≠2时,解⑵ :解 ⑶ : 由分母|x|-3=0,得 x=±3 。所以当x≠ ±3时,例2、当 x 取什么值时,下列分式的值为零 :补充例题解⑴:由分子x+2=0,得 x=-2。而当 x=-2时,分母 2x-5=-4-5≠0。(1)(2)解⑵ :由分子|x|-2=0,得 x=±2。当x=2时,分母 2x+4=4+4≠0。当x=-2时,分母 2x+4=-4+4=0。 例2 甲﹑乙两人从一条公路的某处出发,同向而行.已知甲 每时行a千米,乙每时行b千米,a>b.如果乙提前1时出发,那么甲追上乙需要多少时间?当a=6,b=5时,求甲追上乙所需要的时间? 答:甲追上乙需要 时.当a=6,b=5时,甲追上乙需要
5时.1、当x取什么值时,下列分式有意义?(1) (2) 2、把甲、乙两种饮料按质量比 x∶y 混在一起 , 可以
调制成一种混合饮料. 调制 1kg这种混合饮料需要
多少甲种饮料 ? 解⑴:由分母x-1=0,得 x=1.(2):由分母 x2-9=0,得 x=±3。小测试CB=-10 =2思维园地当x为任意实数时,下列分式一定有意义的是 ( )B归纳小结代数式整式分式分母中必含有字母分母不能为零当分子为零,分母不为零时,
分式值为零。 1、这节课你有哪些收获?
2、目前 ,你学到了哪些式子?能举几个例子吗?
3、区分整式与分式的依据?分式成立有条件吗?1、2 、3。P10分 式 (1)作业同学们再见
3÷4= , 10 ÷ 3= ,
12 ÷11= , -7 ÷2= .
2、在代数式中,整式的除法也可以类似地表示。
试用类似分数的形式表示下列整式的除法:
⑴ 90÷x 可以用式子 来表示。
60÷(x-6)可以用式子 来表示。
(2) n公顷麦田共收小麦m吨,
平均每公顷产量可以用式子 吨来表示. 知识回顾像10a+2b、 、 、2a2这样含有
字母的数学表达式称为代数式.
整式单项式:数与字母或字母与字母的积多项式:几个单项式的和注意:代数式包括整式,也就是说整式是代数式但代数
式就不一定是整式了.有了这些预备知识,这节课我们将要学习另外一种
代数式! 一起努力!16.1.1从分数到分式 为了调查珍稀动物资源,动物专家在p平方米的保护区内找到7只灰熊,那么该保护区
每平方米有____只灰熊.
解:根据题意可知,
该保护区每平方米内灰熊的只数是:7÷p=
? 文林书店库存一批图书,其中一种图书的原价是每册a元,现降价x元销售,当这种图书的库存全部售出时,其销售额为b元,降价销售开始时,文林书店这种图书
的库存量是 。
甲种糖果每千克价格a元,乙种糖果价格b元,取甲种糖果m㎏,乙种糖果n㎏,混合后,平均
每千克价格 元。 轮船在静水中每小时走a千米,水流速度为每小时b千米,轮船在逆流中航行s千米,然后又返回出发地,那么轮船需要的
时间是 小时。 一件商品售价x元,利润率为a%
(a>0),则这种商品每件的成
本是 元。议一议上面题中出现了代数式 它们有什么共同特征?它们与整式有什么不同? 这些代数式都
表示两个整式相除,并且除式中含有字母.像这样的代数式就叫做分式 注解:
(1)分式也是代数式;
(2)分式是两个整式的商,它的形式是 (其中A,B都是
整式并且还要求B是含有字母的整式)
(3)A称为分式的分子,B为分式的分母。 注意:分式中字母的取值不能使分母为零.因为当分母的值为零时,分式就没有意义.关于分式的几点说明分数线有除号和括号的作用,如:分式是两个整式相除的商式。
对于任意一个分式,分母都不为零。1 2你真的清楚了吗?下列各式中,谁是整式?谁是分式?分式整
式想一想下列各式中,哪些是整式?哪些是分式?5x-7, 3x2-1, -5,试着自己举出分式的例子
练一练 课本:1,2(1)当a=1,2时,分别求分式 的值。做一做(2)当a取何值时,分式 无意义?(4)当a取何值时,分式 值为零?
(3)当a取何值时,分式 有意义? 例1 对于分式
(1)当x取什么数时,分式有意义?(2)当x取什么数时,分式的值是零?(3)当x=1时,分式的值是多少?例1 当x取什么值时,下列分式有意义?⑴ , ⑵ , ⑶解⑴:由分母 x-2=0,得 x=2。所以当 x≠2时,解⑵ :解 ⑶ : 由分母|x|-3=0,得 x=±3 。所以当x≠ ±3时,例2、当 x 取什么值时,下列分式的值为零 :补充例题解⑴:由分子x+2=0,得 x=-2。而当 x=-2时,分母 2x-5=-4-5≠0。(1)(2)解⑵ :由分子|x|-2=0,得 x=±2。当x=2时,分母 2x+4=4+4≠0。当x=-2时,分母 2x+4=-4+4=0。 例2 甲﹑乙两人从一条公路的某处出发,同向而行.已知甲 每时行a千米,乙每时行b千米,a>b.如果乙提前1时出发,那么甲追上乙需要多少时间?当a=6,b=5时,求甲追上乙所需要的时间? 答:甲追上乙需要 时.当a=6,b=5时,甲追上乙需要
5时.1、当x取什么值时,下列分式有意义?(1) (2) 2、把甲、乙两种饮料按质量比 x∶y 混在一起 , 可以
调制成一种混合饮料. 调制 1kg这种混合饮料需要
多少甲种饮料 ? 解⑴:由分母x-1=0,得 x=1.(2):由分母 x2-9=0,得 x=±3。小测试CB=-10 =2思维园地当x为任意实数时,下列分式一定有意义的是 ( )B归纳小结代数式整式分式分母中必含有字母分母不能为零当分子为零,分母不为零时,
分式值为零。 1、这节课你有哪些收获?
2、目前 ,你学到了哪些式子?能举几个例子吗?
3、区分整式与分式的依据?分式成立有条件吗?1、2 、3。P10分 式 (1)作业同学们再见
