山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷3(含解析)
文档属性
| 名称 | 山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷3(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 674.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 08:35:42 | ||
图片预览



文档简介
山东省2022年冬季普通高中学业水平合格考试
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.复数的虚部是( )
A. B. C. D.1
2.已知集合,,则( )
A. B. C. D.
3.函数的定义域为
A. B. C. D.
4.命题“,”的否定是( ).
A.,或 B.,或
C., D.,
5.设,则“”是“”的( )
A.充分不必要条件 B.充要不充分条件
C.充分必要条件 D.既不充分 不必要条件
6.( )
A. B. C. D.
7.已知,,且,的夹角为,则( )
A.1 B. C.2 D.
8.已知,给出下列四个不等式:①;②;③;④其中不正确的不等式个数是( )
A.0 B.1 C.2 D.3
9.函数的图象如图所示,则函数的解析式为( )
A. B.
C. D.
10.函数的零点所在的区间为( )
A. B. C. D.
11.已知角A为△ABC的内角,cos A=-,则sin 2A=( )
A.- B.-
C. D.
12.如图,在多面体中,已知是边长为1的正方形,且均为正三角形,,则该多面体的表面积为( )
A. B. C. D.
13.下列函数中,既是偶函数,又在区间上单调递增的函数是( )
A. B. C. D.
14.化简的结果是( )
A. B. C. D.
15.某大学数学系的一 二 三 四年级的人数比为4:3:2:1,要用分层抽样的方法从中抽取一个容量为200的样本,则应抽取的三年级学生的人数为( )
A.80 B.40 C.60 D.20
16.函数是( )
A.周期为的奇函数 B.周期为的奇函数
C.周期为的偶函数 D.周期为的偶函数
17.将一颗质地均匀的骰子先后抛掷两次,观察向上的点数,则点数和为6的概率为( )
A. B. C. D.
18.坛子中放有3个白球、2个黑球,从中不放回地取球2次,每次取1个球,用表示“第一次取得白球”,表示“第二次取得白球”,则和是( )
A.互斥的事件 B.相互独立的事件
C.对立的事件 D.不相互独立的事件
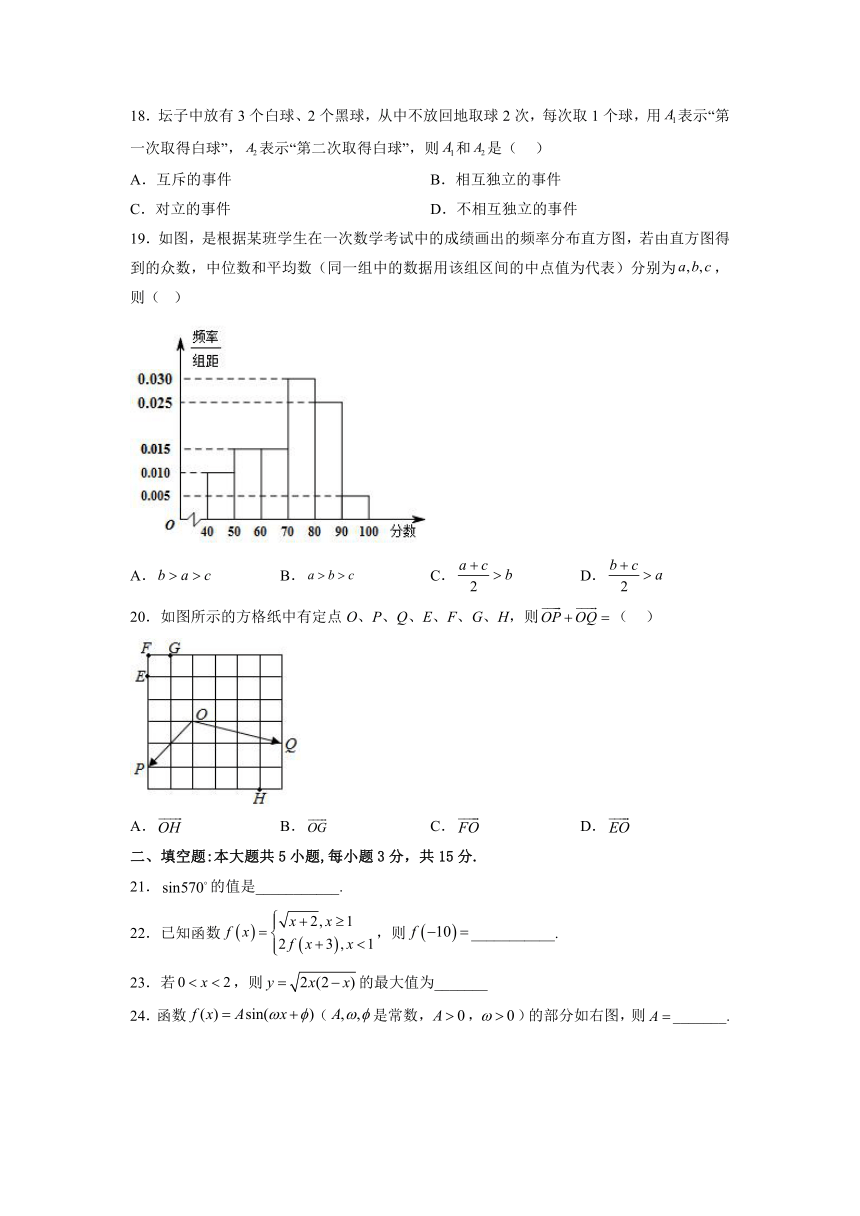
19.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
20.如图所示的方格纸中有定点O、P、Q、E、F、G、H,则( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
21.的值是___________.
22.已知函数,则___________.
23.若,则的最大值为_______
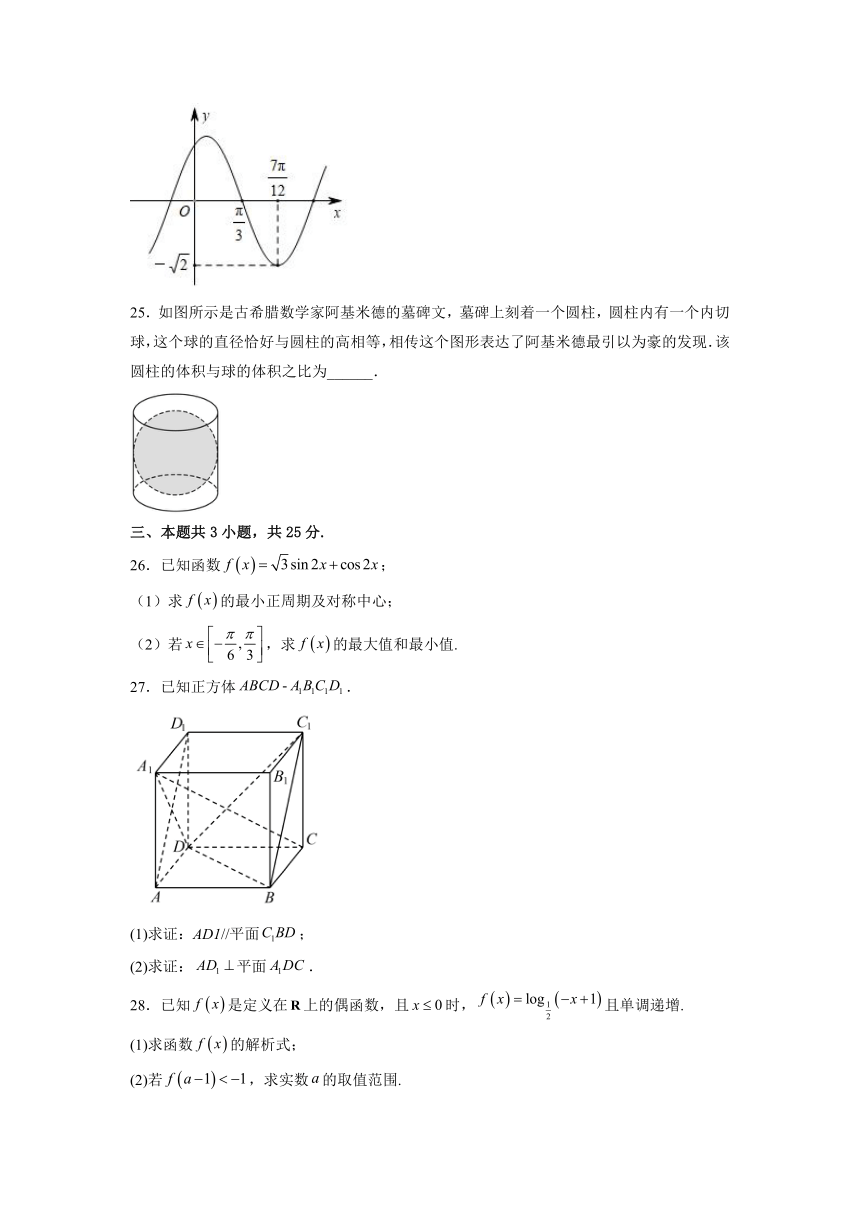
24.函数(是常数,,)的部分如右图,则_______.
25.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为豪的发现.该圆柱的体积与球的体积之比为______.
三、本题共3小题,共25分.
26.已知函数;
(1)求的最小正周期及对称中心;
(2)若,求的最大值和最小值.
27.已知正方体.
(1)求证:AD1//平面;
(2)求证:平面.
28.已知是定义在上的偶函数,且时,且单调递增.
(1)求函数的解析式;
(2)若,求实数的取值范围.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
答案与解析
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.复数的虚部是( )
A. B. C. D.1
【答案】A
【解析】复数的虚部是-1.
故选: A.
2.已知集合,,则( )
A. B. C. D.
【答案】B
【解析】,,则.
故选:B
3.函数的定义域为
A. B. C. D.
【答案】B
【解析】由,得选B
4.命题“,”的否定是( ).
A.,或 B.,或
C., D.,
【答案】B
【解析】根据存在性命题的否定是全称命题可知,
,的否定是,或.
故选:B
5.设,则“”是“”的( )
A.充分不必要条件 B.充要不充分条件
C.充分必要条件 D.既不充分 不必要条件
【答案】A
【解析】由可得,或,
“”能推出“,或”,反之不成立,
所以“”是“”的充分不必要条件,
故选:A
6.( )
A. B. C. D.
【答案】A
【解析】,
故选:A.
7.已知,,且,的夹角为,则( )
A.1 B. C.2 D.
【答案】A
【解析】.
故选:A
8.已知,给出下列四个不等式:①;②;③;④其中不正确的不等式个数是( )
A.0 B.1 C.2 D.3
【答案】C
【解析】因为,所以,
对于①:若,则,故①不正确;
对于②:由可得,所以②不正确;
对于③:,,所以,所以③正确;
对于④:在上单调递增,,所以,故④正确,
所以③④正确,正确的有个,
故选:C
9.函数的图象如图所示,则函数的解析式为( )
A. B.
C. D.
【答案】A
【解析】由图象知,当时,,故排除B,C;又当时,,故排除D.
故选:A.
10.函数的零点所在的区间为( )
A. B. C. D.
【答案】D
【解析】,,,
所以零点在上.
故选:D.
11.已知角A为△ABC的内角,cos A=-,则sin 2A=( )
A.- B.-
C. D.
【答案】A
【解析】∵角A为△ABC的内角,∴0<A<π,
∴sin A= =,
∴sin 2A=2sin Acos A=2××=-.
故选:.
12.如图,在多面体中,已知是边长为1的正方形,且均为正三角形,,则该多面体的表面积为( )
A. B. C. D.
【答案】A
【解析】由于,所以.
依题意,均为正三角形,
所以四边形和四边形是等腰梯形,
两个等腰梯形的高为.
所以多面体的表面积为:.
故选:A
13.下列函数中,既是偶函数,又在区间上单调递增的函数是( )
A. B. C. D.
【答案】D
【解析】是奇函数,不满足题意;
的定义域为,是非奇非偶函数,不满足题意;
是非奇非偶函数,不满足题意;
是偶函数,且在区间上单调递增,满足题意;
故选:D
14.化简的结果是( )
A. B. C. D.
【答案】D
【解析】.
故选:D
15.某大学数学系的一 二 三 四年级的人数比为4:3:2:1,要用分层抽样的方法从中抽取一个容量为200的样本,则应抽取的三年级学生的人数为( )
A.80 B.40 C.60 D.20
【答案】B
【解析】应抽取的三年级学生的人数是,
故选:B.
16.函数是( )
A.周期为的奇函数 B.周期为的奇函数
C.周期为的偶函数 D.周期为的偶函数
【答案】B
【解析】由正切函数性质知:的最小正周期为,
定义域关于原点对称且,即为奇函数.
所以是周期为的奇函数.
故选:B
17.将一颗质地均匀的骰子先后抛掷两次,观察向上的点数,则点数和为6的概率为( )
A. B. C. D.
【答案】B
【解析】一颗质地均匀的正方体骰子先后抛掷2次,可得基本事件的总数为种,
而点数和为的事件为,,,,共5种,
则点数和为的概率为.
故选:B.
18.坛子中放有3个白球、2个黑球,从中不放回地取球2次,每次取1个球,用表示“第一次取得白球”,表示“第二次取得白球”,则和是( )
A.互斥的事件 B.相互独立的事件
C.对立的事件 D.不相互独立的事件
【答案】D
【解析】设白球编号为,黑球的编号为,
从坛子中不放回地取球2次,基本事件有,
,,
,所以和是不相互独立的事件.
基本事件包括“第次取到白球,第次取到白球”,即和可以同时发生,
所以和不是互斥,也不是对立事件.
故选:D
19.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
【答案】B
【解析】由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
20.如图所示的方格纸中有定点O、P、Q、E、F、G、H,则( )
A. B. C. D.
【答案】C
【解析】如图建立平面直角坐标系,则,,,,,,所以,,,,,
所以,所以;
故选:C
二、填空题:本大题共5小题,每小题3分,共15分.
21.的值是___________.
【答案】
【解析】
故答案为:
22.已知函数,则___________.
【答案】32
【解析】
.
故答案为:32
23.若,则的最大值为_______
【答案】
【解析】∵,∴,∴,
当且仅当即时取等号,∴当时,有最大值.
故答案为:.
24.函数(是常数,,)的部分如右图,则_______.
【答案】
【解析】
由图像可知,周期为
所以
将 代入可解得
所以 ,代入 ,可得
化简得 ,所以
25.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为豪的发现.该圆柱的体积与球的体积之比为______.
【答案】
【解析】设球的半径为,则圆柱的底面半径为,高为,,,
故答案为:
三、本题共3小题,共25分.
26.已知函数;
(1)求的最小正周期及对称中心;
(2)若,求的最大值和最小值.
【答案】(1)最小正周期为;对称中心为;(2)最小值为;最大值为2.
【解析】(1)
∴的最小正周期为
令,则
∴的对称中心为
(2),
∴当,即时,的最小值为;
当,即时,的最大值为2.
27.已知正方体.
(1)求证:AD1//平面;
(2)求证:平面.
【答案】(1)证明见解析;
(2)证明见解析.
【解析】(1)在正方体中,,,
则有四边形是平行四边形,有,而平面,平面,
所以平面.
(2)在正方体中,平面,平面,则,
在正方形中,,又,平而,
所以平而.
28.已知是定义在上的偶函数,且时,且单调递增.
(1)求函数的解析式;
(2)若,求实数的取值范围.
【答案】(1)
(2)
【解析】(1)当时,,,
又为上的偶函数,;
.
(2)在上单调递增,又为偶函数,
关于轴对称,且在上单调递减;
又,则由得:,解得:或,
即实数的取值范围为.
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.复数的虚部是( )
A. B. C. D.1
2.已知集合,,则( )
A. B. C. D.
3.函数的定义域为
A. B. C. D.
4.命题“,”的否定是( ).
A.,或 B.,或
C., D.,
5.设,则“”是“”的( )
A.充分不必要条件 B.充要不充分条件
C.充分必要条件 D.既不充分 不必要条件
6.( )
A. B. C. D.
7.已知,,且,的夹角为,则( )
A.1 B. C.2 D.
8.已知,给出下列四个不等式:①;②;③;④其中不正确的不等式个数是( )
A.0 B.1 C.2 D.3
9.函数的图象如图所示,则函数的解析式为( )
A. B.
C. D.
10.函数的零点所在的区间为( )
A. B. C. D.
11.已知角A为△ABC的内角,cos A=-,则sin 2A=( )
A.- B.-
C. D.
12.如图,在多面体中,已知是边长为1的正方形,且均为正三角形,,则该多面体的表面积为( )
A. B. C. D.
13.下列函数中,既是偶函数,又在区间上单调递增的函数是( )
A. B. C. D.
14.化简的结果是( )
A. B. C. D.
15.某大学数学系的一 二 三 四年级的人数比为4:3:2:1,要用分层抽样的方法从中抽取一个容量为200的样本,则应抽取的三年级学生的人数为( )
A.80 B.40 C.60 D.20
16.函数是( )
A.周期为的奇函数 B.周期为的奇函数
C.周期为的偶函数 D.周期为的偶函数
17.将一颗质地均匀的骰子先后抛掷两次,观察向上的点数,则点数和为6的概率为( )
A. B. C. D.
18.坛子中放有3个白球、2个黑球,从中不放回地取球2次,每次取1个球,用表示“第一次取得白球”,表示“第二次取得白球”,则和是( )
A.互斥的事件 B.相互独立的事件
C.对立的事件 D.不相互独立的事件
19.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
20.如图所示的方格纸中有定点O、P、Q、E、F、G、H,则( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
21.的值是___________.
22.已知函数,则___________.
23.若,则的最大值为_______
24.函数(是常数,,)的部分如右图,则_______.
25.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为豪的发现.该圆柱的体积与球的体积之比为______.
三、本题共3小题,共25分.
26.已知函数;
(1)求的最小正周期及对称中心;
(2)若,求的最大值和最小值.
27.已知正方体.
(1)求证:AD1//平面;
(2)求证:平面.
28.已知是定义在上的偶函数,且时,且单调递增.
(1)求函数的解析式;
(2)若,求实数的取值范围.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
答案与解析
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.复数的虚部是( )
A. B. C. D.1
【答案】A
【解析】复数的虚部是-1.
故选: A.
2.已知集合,,则( )
A. B. C. D.
【答案】B
【解析】,,则.
故选:B
3.函数的定义域为
A. B. C. D.
【答案】B
【解析】由,得选B
4.命题“,”的否定是( ).
A.,或 B.,或
C., D.,
【答案】B
【解析】根据存在性命题的否定是全称命题可知,
,的否定是,或.
故选:B
5.设,则“”是“”的( )
A.充分不必要条件 B.充要不充分条件
C.充分必要条件 D.既不充分 不必要条件
【答案】A
【解析】由可得,或,
“”能推出“,或”,反之不成立,
所以“”是“”的充分不必要条件,
故选:A
6.( )
A. B. C. D.
【答案】A
【解析】,
故选:A.
7.已知,,且,的夹角为,则( )
A.1 B. C.2 D.
【答案】A
【解析】.
故选:A
8.已知,给出下列四个不等式:①;②;③;④其中不正确的不等式个数是( )
A.0 B.1 C.2 D.3
【答案】C
【解析】因为,所以,
对于①:若,则,故①不正确;
对于②:由可得,所以②不正确;
对于③:,,所以,所以③正确;
对于④:在上单调递增,,所以,故④正确,
所以③④正确,正确的有个,
故选:C
9.函数的图象如图所示,则函数的解析式为( )
A. B.
C. D.
【答案】A
【解析】由图象知,当时,,故排除B,C;又当时,,故排除D.
故选:A.
10.函数的零点所在的区间为( )
A. B. C. D.
【答案】D
【解析】,,,
所以零点在上.
故选:D.
11.已知角A为△ABC的内角,cos A=-,则sin 2A=( )
A.- B.-
C. D.
【答案】A
【解析】∵角A为△ABC的内角,∴0<A<π,
∴sin A= =,
∴sin 2A=2sin Acos A=2××=-.
故选:.
12.如图,在多面体中,已知是边长为1的正方形,且均为正三角形,,则该多面体的表面积为( )
A. B. C. D.
【答案】A
【解析】由于,所以.
依题意,均为正三角形,
所以四边形和四边形是等腰梯形,
两个等腰梯形的高为.
所以多面体的表面积为:.
故选:A
13.下列函数中,既是偶函数,又在区间上单调递增的函数是( )
A. B. C. D.
【答案】D
【解析】是奇函数,不满足题意;
的定义域为,是非奇非偶函数,不满足题意;
是非奇非偶函数,不满足题意;
是偶函数,且在区间上单调递增,满足题意;
故选:D
14.化简的结果是( )
A. B. C. D.
【答案】D
【解析】.
故选:D
15.某大学数学系的一 二 三 四年级的人数比为4:3:2:1,要用分层抽样的方法从中抽取一个容量为200的样本,则应抽取的三年级学生的人数为( )
A.80 B.40 C.60 D.20
【答案】B
【解析】应抽取的三年级学生的人数是,
故选:B.
16.函数是( )
A.周期为的奇函数 B.周期为的奇函数
C.周期为的偶函数 D.周期为的偶函数
【答案】B
【解析】由正切函数性质知:的最小正周期为,
定义域关于原点对称且,即为奇函数.
所以是周期为的奇函数.
故选:B
17.将一颗质地均匀的骰子先后抛掷两次,观察向上的点数,则点数和为6的概率为( )
A. B. C. D.
【答案】B
【解析】一颗质地均匀的正方体骰子先后抛掷2次,可得基本事件的总数为种,
而点数和为的事件为,,,,共5种,
则点数和为的概率为.
故选:B.
18.坛子中放有3个白球、2个黑球,从中不放回地取球2次,每次取1个球,用表示“第一次取得白球”,表示“第二次取得白球”,则和是( )
A.互斥的事件 B.相互独立的事件
C.对立的事件 D.不相互独立的事件
【答案】D
【解析】设白球编号为,黑球的编号为,
从坛子中不放回地取球2次,基本事件有,
,,
,所以和是不相互独立的事件.
基本事件包括“第次取到白球,第次取到白球”,即和可以同时发生,
所以和不是互斥,也不是对立事件.
故选:D
19.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
【答案】B
【解析】由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
20.如图所示的方格纸中有定点O、P、Q、E、F、G、H,则( )
A. B. C. D.
【答案】C
【解析】如图建立平面直角坐标系,则,,,,,,所以,,,,,
所以,所以;
故选:C
二、填空题:本大题共5小题,每小题3分,共15分.
21.的值是___________.
【答案】
【解析】
故答案为:
22.已知函数,则___________.
【答案】32
【解析】
.
故答案为:32
23.若,则的最大值为_______
【答案】
【解析】∵,∴,∴,
当且仅当即时取等号,∴当时,有最大值.
故答案为:.
24.函数(是常数,,)的部分如右图,则_______.
【答案】
【解析】
由图像可知,周期为
所以
将 代入可解得
所以 ,代入 ,可得
化简得 ,所以
25.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为豪的发现.该圆柱的体积与球的体积之比为______.
【答案】
【解析】设球的半径为,则圆柱的底面半径为,高为,,,
故答案为:
三、本题共3小题,共25分.
26.已知函数;
(1)求的最小正周期及对称中心;
(2)若,求的最大值和最小值.
【答案】(1)最小正周期为;对称中心为;(2)最小值为;最大值为2.
【解析】(1)
∴的最小正周期为
令,则
∴的对称中心为
(2),
∴当,即时,的最小值为;
当,即时,的最大值为2.
27.已知正方体.
(1)求证:AD1//平面;
(2)求证:平面.
【答案】(1)证明见解析;
(2)证明见解析.
【解析】(1)在正方体中,,,
则有四边形是平行四边形,有,而平面,平面,
所以平面.
(2)在正方体中,平面,平面,则,
在正方形中,,又,平而,
所以平而.
28.已知是定义在上的偶函数,且时,且单调递增.
(1)求函数的解析式;
(2)若,求实数的取值范围.
【答案】(1)
(2)
【解析】(1)当时,,,
又为上的偶函数,;
.
(2)在上单调递增,又为偶函数,
关于轴对称,且在上单调递减;
又,则由得:,解得:或,
即实数的取值范围为.
同课章节目录
