山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷4(含解析)
文档属性
| 名称 | 山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷4(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 198.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 08:36:08 | ||
图片预览




文档简介
山东省2022年冬季普通高中学业水平合格考试
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.复数2﹣i的共轭复数是( )
A.2+i B.2﹣i C.﹣2+i D.﹣2﹣i
2.设命题p: k∈N,k2>2k+3,则p的否定为( )
A. k∈N,k2>2k+3 B. k∈N,k2<2k+3
C. k∈N,k2≤2k+3 D. k∈N,k2≤2k+3
3.若<<0,则下列不等式正确的是( )
A.|a|>|b| B.a<b C.a+b>ab D.a3>b3
4.函数的定义域为( )
A.{x|x>﹣1且x≠0} B.{x|x≥﹣1} C.{x|x≥﹣1且x≠0} D.{x|x>﹣1}
5.sinθcosθ=( )
A. B. C.sin2θ D.cos2θ
6.已知扇形的圆心角为,半径为,则此扇形的面积为( )
A. B.π C. D.
7.在△ABC中,点D是BC的中点,则向量=( )
A. B. C. D.
8.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A. B. C. D.
9.设集合A={x|﹣1≤x≤2},B={x|log4x<1},则A∩B=( )
A.{x|x<4} B.{x|﹣1≤x<4} C.{x|0<x≤2} D.{x|0<x<2}
10.一个正方体的顶点都在同一个球的球面上,该正方体的棱长为a,则球的表面积是( )
A. B. C.πa2 D.3πa2
11.已知6个数据5,7,7,8,10,11,则它的标准差是( )
A.2 B.4 C.6 D.8
12.已知cosα= ,且α 为第四象限角,则sinα= ( )
A. B. C. D.
13.某班有男生20人,女生25人,用分层抽样的方法从该班抽取9人参加志愿者活动,则应抽取的女生人数为( )
A.2 B.3 C.4 D.5
14.已知正方体ABCD﹣A1B1C1D1 中,E,F 分别为BC,C1D1 的中点,则( )
A.AF⊥ED1 B.EF⊥CA1 C.A1F⊥BF D.A1F⊥ED1
15.犇犇同学打靶时连续射击三次,事件“至少有一次中靶”的互斥事件是( )
A.三次都中靶 B.只要两次中靶
C.只有一次中靶 D.三次均未中靶
16.函数f(x)=x2,其中x∈[﹣2,1],则f(x)在该区间上的最小值是( )
A.1 B.4 C.﹣4 D.0
17.函数y=﹣lnx的零点所在区间是( )
A.(3,4) B.(2,3) C.(1,2) D.(0,1)
18.函数的单调增区间为( )
A.(0,+∞) B.(﹣∞,0)
C.(﹣∞,0)∪(0,+∞) D.(﹣∞,0),(0,+∞)
19.要得到函数y=sin(x+)图象,只需要将函数y=sinx图象( )
A.向左平移 B.向右平移 C.向左平移 D.向右平移
20.已知a=20.3,b=23,c=2﹣1,那么a,b,c的大小关系为( )
A.a>b>c B.b>a>c C.c>a>b D.c>b>a
二、填空题:本大题共5小题,每小题3分,共15分.
21.函数f(x)=sin(ωx+φ)的部分图像如图所示,则f(x)的最小正周期为 .
22.已知x>0,y>0,且xy=9,则x+y的最小值为 .
23.已知向量,,,则t= .
24.已知,求f(f(﹣1))= .
25.幂函数f(x)=(m2+2m﹣2)xm在区间(0,+∞)上单调递减,则实数m的值为 .
三、解答题:本题共3小题,共25分.
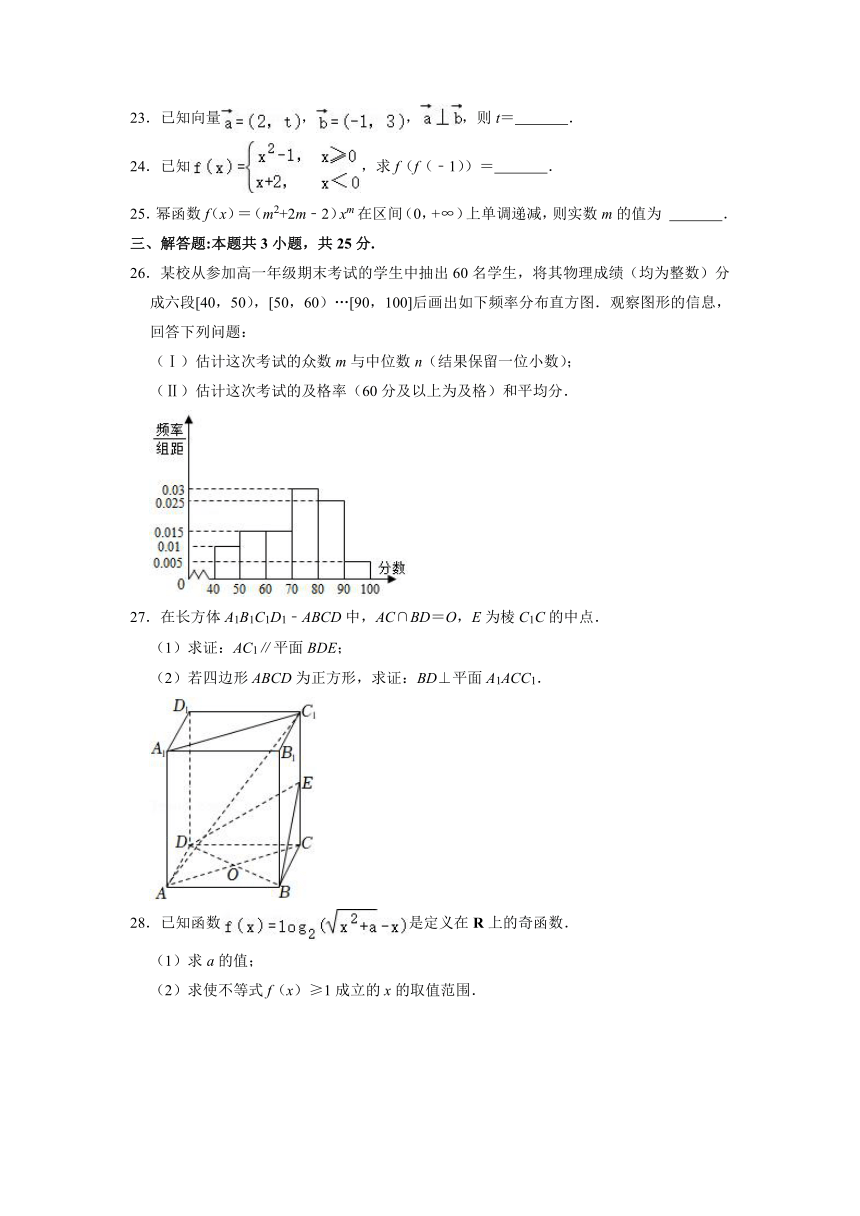
26.某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.
27.在长方体A1B1C1D1﹣ABCD中,AC∩BD=O,E为棱C1C的中点.
(1)求证:AC1∥平面BDE;
(2)若四边形ABCD为正方形,求证:BD⊥平面A1ACC1.
28.已知函数是定义在R上的奇函数.
(1)求a的值;
(2)求使不等式f(x)≥1成立的x的取值范围.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
参考答案与试题解析
一.选择题(共20小题)
1.复数2﹣i的共轭复数是( )
A.2+i B.2﹣i C.﹣2+i D.﹣2﹣i
【解析】复数2﹣i的共轭复数是2+i.
故选:A.
2.设命题p: k∈N,k2>2k+3,则p的否定为( )
A. k∈N,k2>2k+3 B. k∈N,k2<2k+3
C. k∈N,k2≤2k+3 D. k∈N,k2≤2k+3
【解析】命题p: k∈N,k2>2k+3为全称命题,
则p的否定为 k∈N,k2≤2k+3.
故选:D.
3.若<<0,则下列不等式正确的是( )
A.|a|>|b| B.a<b C.a+b>ab D.a3>b3
【解析】因为<<0,所以b<a<0,故B错误,
则﹣b>﹣a>0,所以|﹣b|>|﹣a|,即|b|>|a|,故A错误;
a+b<0,ab>0,所以a+b<ab,故C错误;
因为函数y=x3在R上单调递增,所以a3>b3,故D正确.
故选:D.
4.函数的定义域为( )
A.{x|x>﹣1且x≠0} B.{x|x≥﹣1} C.{x|x≥﹣1且x≠0} D.{x|x>﹣1}
【解析】要使原函数有意义,则:,解得x≥﹣1,且x≠0,
∴原函数的定义域为:{x|x≥﹣1且x≠0}.
故选:C.
5.sinθcosθ=( )
A. B. C.sin2θ D.cos2θ
【解析】sinθcosθ=×2sinθcosθ=sin2θ.
故选:A.
6.已知扇形的圆心角为,半径为,则此扇形的面积为( )
A. B.π C. D.
【解析】因为扇形的圆心角为,半径为,
所以扇形的面积为S==.
故选:B.
7.在△ABC中,点D是BC的中点,则向量=( )
A. B. C. D.
【解析】=.
故选:A.
8.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A. B. C. D.
【解析】甲、乙、丙三名同学站成一排,共有=6种排法,其中甲站在中间的排法有以下两种:乙甲丙、丙甲乙.
因此甲站在中间的概率P=.另解:甲在三个位置是等可能的,所以甲站在中间的概率P=.
故选:C.
9.设集合A={x|﹣1≤x≤2},B={x|log4x<1},则A∩B=( )
A.{x|x<4} B.{x|﹣1≤x<4} C.{x|0<x≤2} D.{x|0<x<2}
【解析】因为B={x|log4x<1}={x|0<x<4},
所以A∩B={x|0<x≤2},
故选:C.
10.一个正方体的顶点都在同一个球的球面上,该正方体的棱长为a,则球的表面积是( )
A. B. C.πa2 D.3πa2
【解析】设球的半径为R,
根据正方体的对角线是球的直径,
可得,所以,
所以球的表面积S=4πR2=3πa2,
故选:D.
11.已知6个数据5,7,7,8,10,11,则它的标准差是( )
A.2 B.4 C.6 D.8
【解析】数据的平均数为,所以标准差为=.
故选:A.
12.已知cosα= ,且α 为第四象限角,则sinα= ( )
A. B. C. D.
【解析】∵α 为第四象限,
∴sinα<0 ,
又∵cosα= ,
∴ .
故选:A.
13.某班有男生20人,女生25人,用分层抽样的方法从该班抽取9人参加志愿者活动,则应抽取的女生人数为( )
A.2 B.3 C.4 D.5
【解析】由题意可得,女生所占的比例为=,
故用分层抽样的方法从该班抽取9人参加志愿者活动,则应抽取的女生人数为9×.
故选:D.
14.已知正方体ABCD﹣A1B1C1D1 中,E,F 分别为BC,C1D1 的中点,则( )
A.AF⊥ED1 B.EF⊥CA1 C.A1F⊥BF D.A1F⊥ED1
【解析】建立如图坐标系,不妨设正方体的棱长为2 .
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
A1(0,0,2),B1(2,0,2),C1(2,2,2),D1(0,2,2),
E(2,1,0),F(1,2,2),
,,,
,
,
,
据此可得只有A1F⊥ED1成立.
故选:D.
15.犇犇同学打靶时连续射击三次,事件“至少有一次中靶”的互斥事件是( )
A.三次都中靶 B.只要两次中靶
C.只有一次中靶 D.三次均未中靶
【解析】事件“至少有一次中靶”包含事件“三次都中靶”,“只要两次中靶”,“只有一次中靶”,
事件“三次均未中靶”与事件“至少有一次中靶”是互斥事件,
故选:D.
16.函数f(x)=x2,其中x∈[﹣2,1],则f(x)在该区间上的最小值是( )
A.1 B.4 C.﹣4 D.0
【解析】函数f(x)=x2是开口向上的抛物线,对称轴为x=0,
∴f(x)=x2在[﹣2,0]上单调递减,在[0,1]单调递增,
∴f(x)min=f(0)=0.
故选:D.
17.函数y=﹣lnx的零点所在区间是( )
A.(3,4) B.(2,3) C.(1,2) D.(0,1)
【解析】函数的定义域为(0,+∞),
∵y′=﹣<0,∴函数y=﹣lnx在(0,+∞)上为减函数,
∵f(2)=1﹣ln2>0,f(3)=,
∴函数y=﹣lnx的零点所在区间是(2,3).
故选:B.
18.函数的单调增区间为( )
A.(0,+∞) B.(﹣∞,0)
C.(﹣∞,0)∪(0,+∞) D.(﹣∞,0),(0,+∞)
【解析】∵函数=1﹣,定义域为{x|x≠0},
且y=的单调递减区间为(﹣∞,0),(0,+∞),
故函数的单调增区间为(﹣∞,0),(0,+∞),
故选:D.
19.要得到函数y=sin(x+)图象,只需要将函数y=sinx图象( )
A.向左平移 B.向右平移 C.向左平移 D.向右平移
【解析】要得到函数y=sin(x+)图象,只需要将函数y=sinx图象向左平移个单位即可,
故选:A.
20.已知a=20.3,b=23,c=2﹣1,那么a,b,c的大小关系为( )
A.a>b>c B.b>a>c C.c>a>b D.c>b>a
【解析】∵函数y=2x在R上单调递增,3>0.3>﹣1,a=20.3 ,b=23 ,c=2﹣1,
∴b>a>c,
故选:B.
二.填空题(共5小题)
21.函数f(x)=sin(ωx+φ)的部分图像如图所示,则f(x)的最小正周期为 2 .
【解析】设函数f(x)=sin(ωx+φ)的最小正周期为T,
由图像可知,,所以T=2.
故答案为:2.
22.已知x>0,y>0,且xy=9,则x+y的最小值为 6 .
【解析】因为x>0,y>0,且xy=9,
所以x+y≥2=6,当且仅当x=y=3时取等号,
所以x+y的最小值为6.
故答案为:6.
23.已知向量,,,则t= .
【解析】根据题意,向量,,
若,则 =﹣2+3t=0,解可得t=,
故答案为:.
24.已知,求f(f(﹣1))= 0 .
【解析】∵,
∴f(﹣1)=﹣1+2=1,
∴f(f(﹣1))=f(1)=12﹣1=0,
故答案为:0.
25.幂函数f(x)=(m2+2m﹣2)xm在区间(0,+∞)上单调递减,则实数m的值为 ﹣3 .
【解析】∵幂函数f(x)=(m2+2m﹣2)xm在区间(0,+∞)上单调递减,
∴,∴m=﹣3,
故答案为:﹣3.
三.解答题(共3小题)
26.某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.
【解析】(Ⅰ)众数是最高小矩形中点的横坐标,所以众数为m=75(分);(3分)
前三个小矩形面积为0.01×10+0.015×10+0.015×10=0.4,
∵中位数要平分直方图的面积,∴(7分)
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 (0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75% (11分)
利用组中值估算抽样学生的平均分45 f1+55 f2+65 f3+75 f4+85 f5+95 f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71分.(14分)
27.在长方体A1B1C1D1﹣ABCD中,AC∩BD=O,E为棱C1C的中点.
(1)求证:AC1∥平面BDE;
(2)若四边形ABCD为正方形,求证:BD⊥平面A1ACC1.
【解答】证明:(1)连结OE,在长方体A1B1C1D1﹣ABCD中,
四边形ABCD为矩形,∴O是AC中点,
∵E为棱C1C的中点,∴OE∥AC1,
∵OE 平面BDE,AC1 平面BDE,
∴AC1∥平面BDE.
(2)解:在长方体A1B1C1D1﹣ABCD中,CC1⊥平面ABCD,
∵BD 平面ABCD,∴CC1⊥BD,
∵四边形ABCD是正方形,∴BD⊥AC,
∵AC 平面ACC1,CC1 平面ACC1,AC∩CC1=C,
∴BD⊥平面A1ACC1.
28.已知函数是定义在R上的奇函数.
(1)求a的值;
(2)求使不等式f(x)≥1成立的x的取值范围.
【解析】(1)根据题意,函数是定义在R上的奇函数,
必有f(0)=log2=0,解可得a=1,
当a=1时,f(x)=log2(﹣x),满足定义域为R,
且f(﹣x)+f(x)=log2(+x)+log2(﹣x)=0,f(x)为奇函数,符合题意,
故a=1;
(2)根据题意,由(1)的结论,f(x)=log2(﹣x),
则f(x)≥1 log2(﹣x)≥log22 ﹣x≥2,
解可得x≤﹣,即x的取值范围为(﹣∞,﹣].
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.复数2﹣i的共轭复数是( )
A.2+i B.2﹣i C.﹣2+i D.﹣2﹣i
2.设命题p: k∈N,k2>2k+3,则p的否定为( )
A. k∈N,k2>2k+3 B. k∈N,k2<2k+3
C. k∈N,k2≤2k+3 D. k∈N,k2≤2k+3
3.若<<0,则下列不等式正确的是( )
A.|a|>|b| B.a<b C.a+b>ab D.a3>b3
4.函数的定义域为( )
A.{x|x>﹣1且x≠0} B.{x|x≥﹣1} C.{x|x≥﹣1且x≠0} D.{x|x>﹣1}
5.sinθcosθ=( )
A. B. C.sin2θ D.cos2θ
6.已知扇形的圆心角为,半径为,则此扇形的面积为( )
A. B.π C. D.
7.在△ABC中,点D是BC的中点,则向量=( )
A. B. C. D.
8.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A. B. C. D.
9.设集合A={x|﹣1≤x≤2},B={x|log4x<1},则A∩B=( )
A.{x|x<4} B.{x|﹣1≤x<4} C.{x|0<x≤2} D.{x|0<x<2}
10.一个正方体的顶点都在同一个球的球面上,该正方体的棱长为a,则球的表面积是( )
A. B. C.πa2 D.3πa2
11.已知6个数据5,7,7,8,10,11,则它的标准差是( )
A.2 B.4 C.6 D.8
12.已知cosα= ,且α 为第四象限角,则sinα= ( )
A. B. C. D.
13.某班有男生20人,女生25人,用分层抽样的方法从该班抽取9人参加志愿者活动,则应抽取的女生人数为( )
A.2 B.3 C.4 D.5
14.已知正方体ABCD﹣A1B1C1D1 中,E,F 分别为BC,C1D1 的中点,则( )
A.AF⊥ED1 B.EF⊥CA1 C.A1F⊥BF D.A1F⊥ED1
15.犇犇同学打靶时连续射击三次,事件“至少有一次中靶”的互斥事件是( )
A.三次都中靶 B.只要两次中靶
C.只有一次中靶 D.三次均未中靶
16.函数f(x)=x2,其中x∈[﹣2,1],则f(x)在该区间上的最小值是( )
A.1 B.4 C.﹣4 D.0
17.函数y=﹣lnx的零点所在区间是( )
A.(3,4) B.(2,3) C.(1,2) D.(0,1)
18.函数的单调增区间为( )
A.(0,+∞) B.(﹣∞,0)
C.(﹣∞,0)∪(0,+∞) D.(﹣∞,0),(0,+∞)
19.要得到函数y=sin(x+)图象,只需要将函数y=sinx图象( )
A.向左平移 B.向右平移 C.向左平移 D.向右平移
20.已知a=20.3,b=23,c=2﹣1,那么a,b,c的大小关系为( )
A.a>b>c B.b>a>c C.c>a>b D.c>b>a
二、填空题:本大题共5小题,每小题3分,共15分.
21.函数f(x)=sin(ωx+φ)的部分图像如图所示,则f(x)的最小正周期为 .
22.已知x>0,y>0,且xy=9,则x+y的最小值为 .
23.已知向量,,,则t= .
24.已知,求f(f(﹣1))= .
25.幂函数f(x)=(m2+2m﹣2)xm在区间(0,+∞)上单调递减,则实数m的值为 .
三、解答题:本题共3小题,共25分.
26.某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.
27.在长方体A1B1C1D1﹣ABCD中,AC∩BD=O,E为棱C1C的中点.
(1)求证:AC1∥平面BDE;
(2)若四边形ABCD为正方形,求证:BD⊥平面A1ACC1.
28.已知函数是定义在R上的奇函数.
(1)求a的值;
(2)求使不等式f(x)≥1成立的x的取值范围.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
参考答案与试题解析
一.选择题(共20小题)
1.复数2﹣i的共轭复数是( )
A.2+i B.2﹣i C.﹣2+i D.﹣2﹣i
【解析】复数2﹣i的共轭复数是2+i.
故选:A.
2.设命题p: k∈N,k2>2k+3,则p的否定为( )
A. k∈N,k2>2k+3 B. k∈N,k2<2k+3
C. k∈N,k2≤2k+3 D. k∈N,k2≤2k+3
【解析】命题p: k∈N,k2>2k+3为全称命题,
则p的否定为 k∈N,k2≤2k+3.
故选:D.
3.若<<0,则下列不等式正确的是( )
A.|a|>|b| B.a<b C.a+b>ab D.a3>b3
【解析】因为<<0,所以b<a<0,故B错误,
则﹣b>﹣a>0,所以|﹣b|>|﹣a|,即|b|>|a|,故A错误;
a+b<0,ab>0,所以a+b<ab,故C错误;
因为函数y=x3在R上单调递增,所以a3>b3,故D正确.
故选:D.
4.函数的定义域为( )
A.{x|x>﹣1且x≠0} B.{x|x≥﹣1} C.{x|x≥﹣1且x≠0} D.{x|x>﹣1}
【解析】要使原函数有意义,则:,解得x≥﹣1,且x≠0,
∴原函数的定义域为:{x|x≥﹣1且x≠0}.
故选:C.
5.sinθcosθ=( )
A. B. C.sin2θ D.cos2θ
【解析】sinθcosθ=×2sinθcosθ=sin2θ.
故选:A.
6.已知扇形的圆心角为,半径为,则此扇形的面积为( )
A. B.π C. D.
【解析】因为扇形的圆心角为,半径为,
所以扇形的面积为S==.
故选:B.
7.在△ABC中,点D是BC的中点,则向量=( )
A. B. C. D.
【解析】=.
故选:A.
8.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A. B. C. D.
【解析】甲、乙、丙三名同学站成一排,共有=6种排法,其中甲站在中间的排法有以下两种:乙甲丙、丙甲乙.
因此甲站在中间的概率P=.另解:甲在三个位置是等可能的,所以甲站在中间的概率P=.
故选:C.
9.设集合A={x|﹣1≤x≤2},B={x|log4x<1},则A∩B=( )
A.{x|x<4} B.{x|﹣1≤x<4} C.{x|0<x≤2} D.{x|0<x<2}
【解析】因为B={x|log4x<1}={x|0<x<4},
所以A∩B={x|0<x≤2},
故选:C.
10.一个正方体的顶点都在同一个球的球面上,该正方体的棱长为a,则球的表面积是( )
A. B. C.πa2 D.3πa2
【解析】设球的半径为R,
根据正方体的对角线是球的直径,
可得,所以,
所以球的表面积S=4πR2=3πa2,
故选:D.
11.已知6个数据5,7,7,8,10,11,则它的标准差是( )
A.2 B.4 C.6 D.8
【解析】数据的平均数为,所以标准差为=.
故选:A.
12.已知cosα= ,且α 为第四象限角,则sinα= ( )
A. B. C. D.
【解析】∵α 为第四象限,
∴sinα<0 ,
又∵cosα= ,
∴ .
故选:A.
13.某班有男生20人,女生25人,用分层抽样的方法从该班抽取9人参加志愿者活动,则应抽取的女生人数为( )
A.2 B.3 C.4 D.5
【解析】由题意可得,女生所占的比例为=,
故用分层抽样的方法从该班抽取9人参加志愿者活动,则应抽取的女生人数为9×.
故选:D.
14.已知正方体ABCD﹣A1B1C1D1 中,E,F 分别为BC,C1D1 的中点,则( )
A.AF⊥ED1 B.EF⊥CA1 C.A1F⊥BF D.A1F⊥ED1
【解析】建立如图坐标系,不妨设正方体的棱长为2 .
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
A1(0,0,2),B1(2,0,2),C1(2,2,2),D1(0,2,2),
E(2,1,0),F(1,2,2),
,,,
,
,
,
据此可得只有A1F⊥ED1成立.
故选:D.
15.犇犇同学打靶时连续射击三次,事件“至少有一次中靶”的互斥事件是( )
A.三次都中靶 B.只要两次中靶
C.只有一次中靶 D.三次均未中靶
【解析】事件“至少有一次中靶”包含事件“三次都中靶”,“只要两次中靶”,“只有一次中靶”,
事件“三次均未中靶”与事件“至少有一次中靶”是互斥事件,
故选:D.
16.函数f(x)=x2,其中x∈[﹣2,1],则f(x)在该区间上的最小值是( )
A.1 B.4 C.﹣4 D.0
【解析】函数f(x)=x2是开口向上的抛物线,对称轴为x=0,
∴f(x)=x2在[﹣2,0]上单调递减,在[0,1]单调递增,
∴f(x)min=f(0)=0.
故选:D.
17.函数y=﹣lnx的零点所在区间是( )
A.(3,4) B.(2,3) C.(1,2) D.(0,1)
【解析】函数的定义域为(0,+∞),
∵y′=﹣<0,∴函数y=﹣lnx在(0,+∞)上为减函数,
∵f(2)=1﹣ln2>0,f(3)=,
∴函数y=﹣lnx的零点所在区间是(2,3).
故选:B.
18.函数的单调增区间为( )
A.(0,+∞) B.(﹣∞,0)
C.(﹣∞,0)∪(0,+∞) D.(﹣∞,0),(0,+∞)
【解析】∵函数=1﹣,定义域为{x|x≠0},
且y=的单调递减区间为(﹣∞,0),(0,+∞),
故函数的单调增区间为(﹣∞,0),(0,+∞),
故选:D.
19.要得到函数y=sin(x+)图象,只需要将函数y=sinx图象( )
A.向左平移 B.向右平移 C.向左平移 D.向右平移
【解析】要得到函数y=sin(x+)图象,只需要将函数y=sinx图象向左平移个单位即可,
故选:A.
20.已知a=20.3,b=23,c=2﹣1,那么a,b,c的大小关系为( )
A.a>b>c B.b>a>c C.c>a>b D.c>b>a
【解析】∵函数y=2x在R上单调递增,3>0.3>﹣1,a=20.3 ,b=23 ,c=2﹣1,
∴b>a>c,
故选:B.
二.填空题(共5小题)
21.函数f(x)=sin(ωx+φ)的部分图像如图所示,则f(x)的最小正周期为 2 .
【解析】设函数f(x)=sin(ωx+φ)的最小正周期为T,
由图像可知,,所以T=2.
故答案为:2.
22.已知x>0,y>0,且xy=9,则x+y的最小值为 6 .
【解析】因为x>0,y>0,且xy=9,
所以x+y≥2=6,当且仅当x=y=3时取等号,
所以x+y的最小值为6.
故答案为:6.
23.已知向量,,,则t= .
【解析】根据题意,向量,,
若,则 =﹣2+3t=0,解可得t=,
故答案为:.
24.已知,求f(f(﹣1))= 0 .
【解析】∵,
∴f(﹣1)=﹣1+2=1,
∴f(f(﹣1))=f(1)=12﹣1=0,
故答案为:0.
25.幂函数f(x)=(m2+2m﹣2)xm在区间(0,+∞)上单调递减,则实数m的值为 ﹣3 .
【解析】∵幂函数f(x)=(m2+2m﹣2)xm在区间(0,+∞)上单调递减,
∴,∴m=﹣3,
故答案为:﹣3.
三.解答题(共3小题)
26.某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.
【解析】(Ⅰ)众数是最高小矩形中点的横坐标,所以众数为m=75(分);(3分)
前三个小矩形面积为0.01×10+0.015×10+0.015×10=0.4,
∵中位数要平分直方图的面积,∴(7分)
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 (0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75% (11分)
利用组中值估算抽样学生的平均分45 f1+55 f2+65 f3+75 f4+85 f5+95 f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71分.(14分)
27.在长方体A1B1C1D1﹣ABCD中,AC∩BD=O,E为棱C1C的中点.
(1)求证:AC1∥平面BDE;
(2)若四边形ABCD为正方形,求证:BD⊥平面A1ACC1.
【解答】证明:(1)连结OE,在长方体A1B1C1D1﹣ABCD中,
四边形ABCD为矩形,∴O是AC中点,
∵E为棱C1C的中点,∴OE∥AC1,
∵OE 平面BDE,AC1 平面BDE,
∴AC1∥平面BDE.
(2)解:在长方体A1B1C1D1﹣ABCD中,CC1⊥平面ABCD,
∵BD 平面ABCD,∴CC1⊥BD,
∵四边形ABCD是正方形,∴BD⊥AC,
∵AC 平面ACC1,CC1 平面ACC1,AC∩CC1=C,
∴BD⊥平面A1ACC1.
28.已知函数是定义在R上的奇函数.
(1)求a的值;
(2)求使不等式f(x)≥1成立的x的取值范围.
【解析】(1)根据题意,函数是定义在R上的奇函数,
必有f(0)=log2=0,解可得a=1,
当a=1时,f(x)=log2(﹣x),满足定义域为R,
且f(﹣x)+f(x)=log2(+x)+log2(﹣x)=0,f(x)为奇函数,符合题意,
故a=1;
(2)根据题意,由(1)的结论,f(x)=log2(﹣x),
则f(x)≥1 log2(﹣x)≥log22 ﹣x≥2,
解可得x≤﹣,即x的取值范围为(﹣∞,﹣].
同课章节目录
