山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷2(含解析)
文档属性
| 名称 | 山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷2(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 08:37:07 | ||
图片预览



文档简介
山东省2022年冬季普通高中学业水平合格考试
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,,则( )
A. B. C. D.
2.己知命题p:,.则命题p的否定是( )
A., B.,
C., D.,
3.口袋中共有2个白球2个黑球,从中随机取出两个球,则两个球颜色不同的概率为( )
A. B. C. D.
4.“且”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.( )
A.1 B. C. D.
6.若一个正方体的体对角线长为a,则这个正方体的全面积为( )
A. B. C. D.
7.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法抽取一个容量为n的样本,已知从女学生中抽取的人数为80,则n为( )
A.16 B.96 C.192 D.112
8.已知 ,且 为第四象限角,则 ( )
A. B.
C. D.
9.已知向量,若,则( )
A. B. C. D.
10.函数的图象的一个对称轴方程是( )
A. B. C. D.
11.在中,若,则-定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
12.设a、b、c表示三条直线,,表示两个平面,下面命题中不正确的是( )
A. B.
C. D.
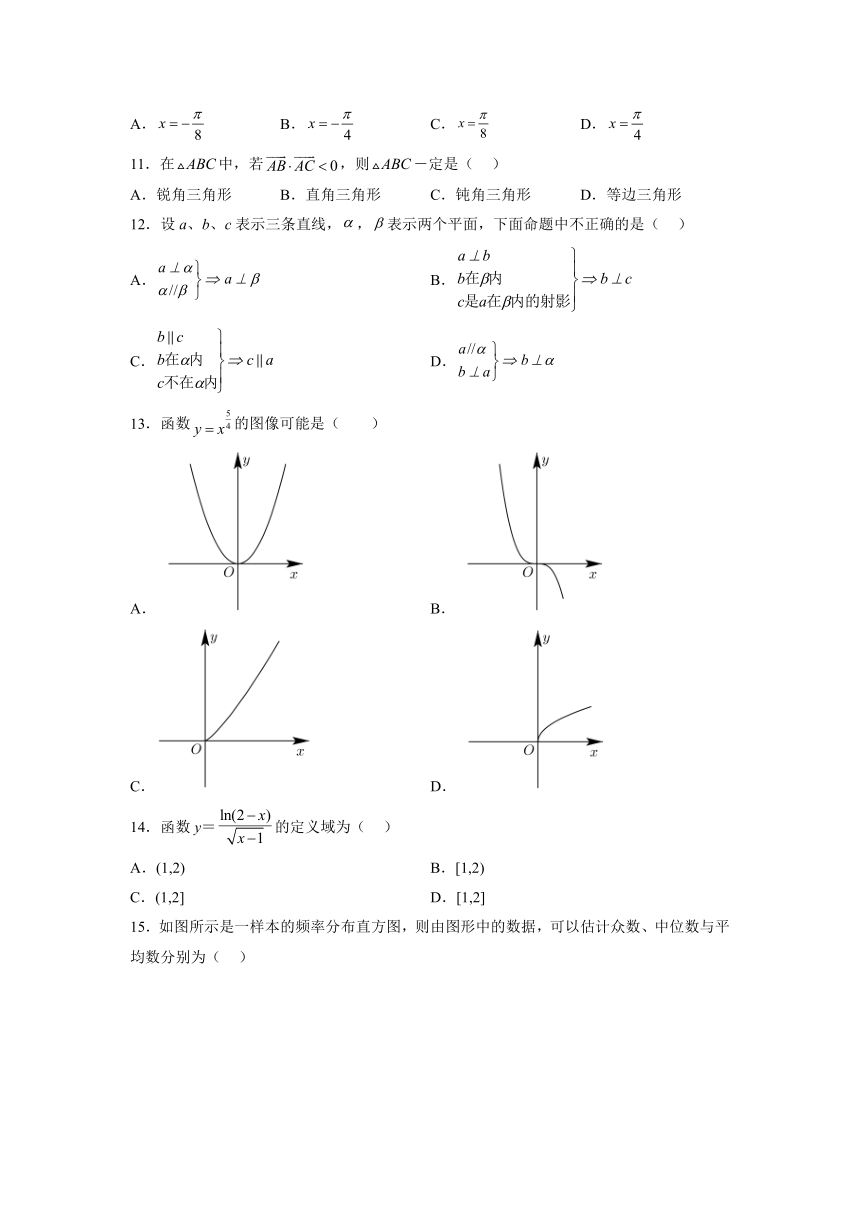
13.函数的图像可能是( )
A. B.
C. D.
14.函数y=的定义域为( )
A.(1,2) B.[1,2)
C.(1,2] D.[1,2]
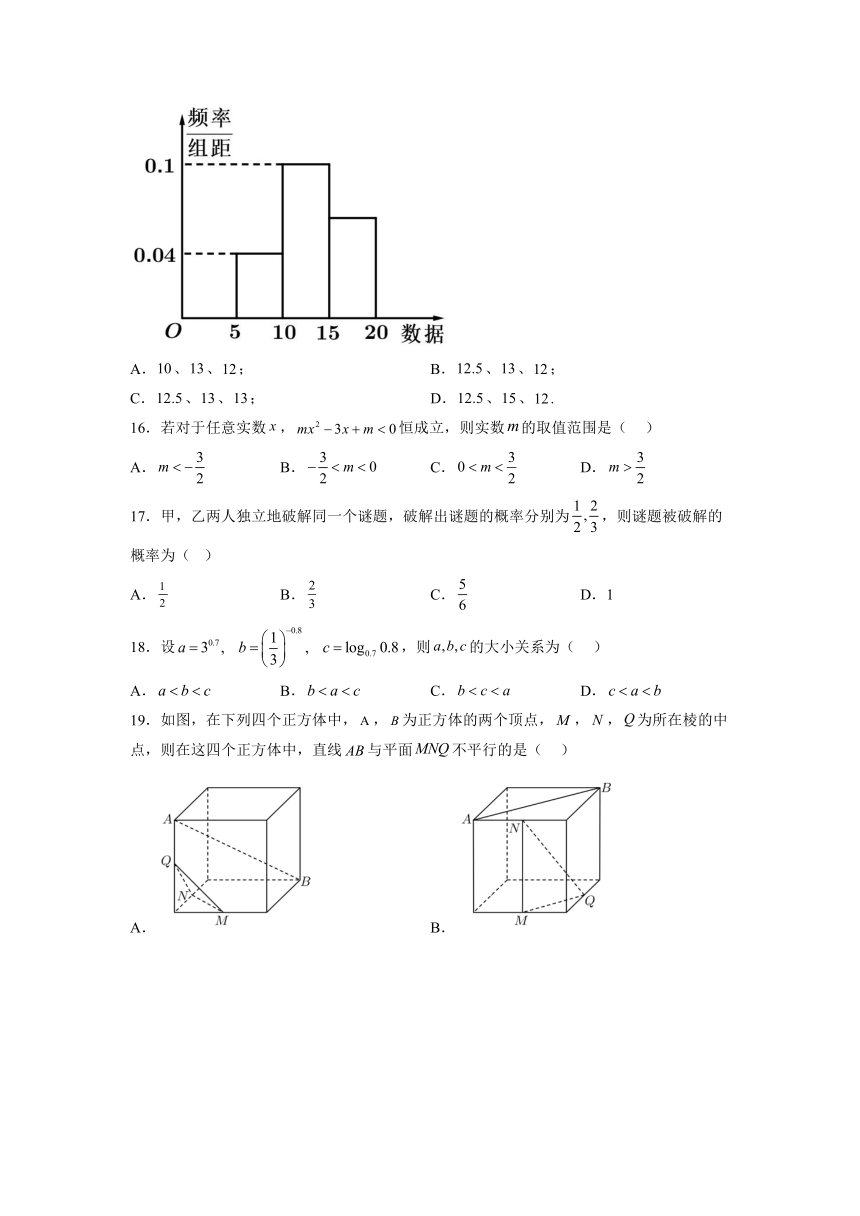
15.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数、中位数与平均数分别为( )
A.、、; B.、、;
C.、、; D.、、.
16.若对于任意实数,恒成立,则实数的取值范围是( )
A. B. C. D.
17.甲,乙两人独立地破解同一个谜题,破解出谜题的概率分别为,则谜题被破解的概率为( )
A. B. C. D.1
18.设,则的大小关系为( )
A. B. C. D.
19.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是( )
A. B.
C. D.
20.若函数是定义在上的偶函数,且在上是增函数,,则不等式的解集为( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
21.已知z=2+i(其中i为虚数单位),则=______.
22.已知函数,则__________.
23.__________.
24.已知,且,则xy的最大值是___________.
25.用一个平面去截直三棱柱,交分别于点. 若,则截面的形状可以为________.(把你认为可能的结果的序号填在横线上)
①一般的平行四边形;②矩形;③菱形;④正方形;⑤梯形
三、解答题:本题共3小题,共25分.
26.已知函数.
(1)求函数的单调递减区间及其图象的对称中心;
(2)已知函数的图象经过先平移后伸缩得到的图象,试写出其变换过程.
27.A B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
B同学的成绩不慎被墨迹污染(,分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差s2=19,求m,n.
28.设函数且是定义域为的奇函数;
(1)若,判断的单调性并求不等式的解集;
(2)若,且,求在上的最小值.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
答案与解析
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,,则( )
A. B. C. D.
【答案】D
【解析】由已知可得.
故选:D.
2.己知命题p:,.则命题p的否定是( )
A., B.,
C., D.,
【答案】A
【解析】特称命题的否定是全称命题.
原命题的否定是:,.
故选:A.
3.口袋中共有2个白球2个黑球,从中随机取出两个球,则两个球颜色不同的概率为( )
A. B. C. D.
【答案】A
【解析】设2个白球分别为,2个黑球为,从中随机取出两个球,则所有可能的情况有,,,,,共6种情况,
其中两个球颜色不同的情况有,,,共4种情况,故两个球颜色不同的概率为
故选:A
4.“且”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【解析】充分性: 且,则,充分性成立;必要性: 若,则且,或且,必要性不成立.故“且”是“”的充分而不必要条件.
故选:A.
5.( )
A.1 B. C. D.
【答案】A
【解析】。
故选;A。
6.若一个正方体的体对角线长为a,则这个正方体的全面积为( )
A. B. C. D.
【答案】A
【解析】设正方体的棱长为x,则,即,
所以正方体的全面积为.
故选:A
7.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法抽取一个容量为n的样本,已知从女学生中抽取的人数为80,则n为( )
A.16 B.96 C.192 D.112
【答案】C
【解析】由于采用分层抽样,
每种样本类型中抽取的人数比例为
则
故选:C.
8.已知 ,且 为第四象限角,则 ( )
A. B.
C. D.
【答案】A
【解析】 为第四象限,
,
故选:A
9.已知向量,若,则( )
A. B. C. D.
【答案】D
【解析】因为,,
所以,解得.
故选:D.
10.函数的图象的一个对称轴方程是( )
A. B. C. D.
【答案】C
【解析】对于函数,令,
解得,故函数的对称轴方程为,
令,可知函数的一条对称轴为.
故选:C
11.在中,若,则-定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
【答案】C
【解析】由向量的数量积的运算公式,可得,即,
因为,所以为钝角,所以-定是钝角三角形.
故选:C.
12.设a、b、c表示三条直线,,表示两个平面,下面命题中不正确的是( )
A. B.
C. D.
【答案】D
【解析】A选项:因为,所以垂直平面内的所有直线,又∥,所以平面内的任意直线在平面内都存在直线与之平行,所以垂直平面内的任意直线,,A正确;
B选项:
如图,为直线,为斜足,过作,所以为在平面内的投影,因为,,所以,又,,平面,平面,所以平面,又平面,所以,B正确;
C选项:根据线面平行的判定定理可得C正确;
D选项:不能说明和平面内的直线都垂直,所以D错.
故选;D.
13.函数的图像可能是( )
A. B.
C. D.
【答案】C
14.函数y=的定义域为( )
A.(1,2) B.[1,2)
C.(1,2] D.[1,2]
【答案】A
【解析】由题意得,解得1故选:A.
15.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数、中位数与平均数分别为( )
A.、、; B.、、;
C.、、; D.、、.
【答案】C
【解析】众数是频率分布直方图中最高矩形的底边中点的横坐标,则众数是,
中位数是把频率分布直方图分成两个面积相等部分的平行于轴的直线的横坐标,
第一个矩形的面积是,第三个矩形的面积是,
故将第二个矩形分成即可,中位数是,
平均数为,
故选:C.
16.若对于任意实数,恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】A
【解析】对于任意实数,不等式恒成立,
当时,,不恒成立,不符合题意;
当时,应满足,即,解得;
综上,实数的取值范围是.
故选:A.
17.甲,乙两人独立地破解同一个谜题,破解出谜题的概率分别为,则谜题被破解的概率为( )
A. B. C. D.1
【答案】C
【解析】设甲,乙两人破解出谜题分别为事件,
则有,则,
谜题被破解的对立事件是甲乙都没有破解谜题,
则.
故选:C.
18.设,则的大小关系为( )
A. B. C. D.
【答案】D
【解析】因为,
,
,
所以.
故选:D.
19.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是( )
A. B.
C. D.
【答案】A
【解析】对A,如图,易得平面平面,但平面与相交,故直线与平面不平行;
对B,如图,为所在棱的中点,根据中位线的性质有,且,,故平行四边形,故,故,故直线与平面平行.
对C,根据中位线与平行四边形的性质,同理可得,直线与平面平行;
对D,根据中位线与平行四边形的性质,同理可得,直线与平面平行;
故选:A
20.若函数是定义在上的偶函数,且在上是增函数,,则不等式的解集为( )
A. B. C. D.
【答案】A
【解析】函数是定义在上的偶函数,可得,
由在,上是增函数,可得在,是减函数,
又(2),可得不等式即为
即有,即,解得,所以解集为.
故:A.
二、填空题:本大题共5小题,每小题3分,共15分.
21.已知z=2+i(其中i为虚数单位),则=______.
【答案】
【解析】因,所以.
故答案为:
22.已知函数,则__________.
【答案】32
【解析】由题意可得:,则
故答案为:32.
23.__________.
【答案】
【解析】.
故答案为:.
24.已知,且,则xy的最大值是___________.
【答案】4
【解析】x>0,y>0,且,则,
解得,当且仅当时取等号,
所以xy的最大值是.
故答案为:4
25.用一个平面去截直三棱柱,交分别于点. 若,则截面的形状可以为________.(把你认为可能的结果的序号填在横线上)
①一般的平行四边形;②矩形;③菱形;④正方形;⑤梯形
【答案】②④⑤
【解析】为直三棱柱,则面面,截面过面、面,则交线,
当不与平行时,此时截得的EH不平行于FG,四边形为梯形;
当时,此时截得的,,
当时,四边形为矩形;当时,四边形为正方形;
故答案为:②④⑤
三、解答题:本题共3小题,共25分.
26.已知函数.
(1)求函数的单调递减区间及其图象的对称中心;
(2)已知函数的图象经过先平移后伸缩得到的图象,试写出其变换过程.
【答案】(1)单调递减区间为,,对称中心为,.
(2)答案见解析
【解析】(1)令,,得,,
因此函数的单调递减区间是,.
令,,得,,因此函数图象的对称中心是,.
(2)
,先将函数的图象向右平移个单位长度,得到的图象,
接着把图象上所有点的纵坐标不变,横坐标伸长为原来的2倍,得到的图象,
最后把图象上所有点的横坐标不变,纵坐标伸长为原来的2倍,得到的图象.
27.A B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
B同学的成绩不慎被墨迹污染(,分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差s2=19,求m,n.
【答案】(1)茎叶图答案见解析,选派B同学参加数学竞赛更好,理由见解析;(2)m=8,n=0.
【解析】(1)A,B两同学参加了8次测验,成绩(单位:分)茎叶图如下:
由茎叶图可知,B同学的平均成绩高于A同学的平均成绩,
所以选派B同学参加数学竞赛更好;
(2)因为,
所以①,
因为,
所以②,
联立①②解得,.
28.设函数且是定义域为的奇函数;
(1)若,判断的单调性并求不等式的解集;
(2)若,且,求在上的最小值.
【答案】(1)增函数,;(2).
【解析】(1)因为函数且是定义域为的奇函数,
可得,从而得,即
当时,函数,
满足,所以,
由,可得且,解得,所以是增函数,
又由,可得,
所以,解得,即不等式的解集是.
(2)由(1)知,,
因为,即,解得,
故,
令,则在上是增函数,故,
即,
此时函数的对称轴为,且开口向上,
所以当,函数取得最小值,最小值为,
即函数的最小值为.
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,,则( )
A. B. C. D.
2.己知命题p:,.则命题p的否定是( )
A., B.,
C., D.,
3.口袋中共有2个白球2个黑球,从中随机取出两个球,则两个球颜色不同的概率为( )
A. B. C. D.
4.“且”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.( )
A.1 B. C. D.
6.若一个正方体的体对角线长为a,则这个正方体的全面积为( )
A. B. C. D.
7.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法抽取一个容量为n的样本,已知从女学生中抽取的人数为80,则n为( )
A.16 B.96 C.192 D.112
8.已知 ,且 为第四象限角,则 ( )
A. B.
C. D.
9.已知向量,若,则( )
A. B. C. D.
10.函数的图象的一个对称轴方程是( )
A. B. C. D.
11.在中,若,则-定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
12.设a、b、c表示三条直线,,表示两个平面,下面命题中不正确的是( )
A. B.
C. D.
13.函数的图像可能是( )
A. B.
C. D.
14.函数y=的定义域为( )
A.(1,2) B.[1,2)
C.(1,2] D.[1,2]
15.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数、中位数与平均数分别为( )
A.、、; B.、、;
C.、、; D.、、.
16.若对于任意实数,恒成立,则实数的取值范围是( )
A. B. C. D.
17.甲,乙两人独立地破解同一个谜题,破解出谜题的概率分别为,则谜题被破解的概率为( )
A. B. C. D.1
18.设,则的大小关系为( )
A. B. C. D.
19.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是( )
A. B.
C. D.
20.若函数是定义在上的偶函数,且在上是增函数,,则不等式的解集为( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
21.已知z=2+i(其中i为虚数单位),则=______.
22.已知函数,则__________.
23.__________.
24.已知,且,则xy的最大值是___________.
25.用一个平面去截直三棱柱,交分别于点. 若,则截面的形状可以为________.(把你认为可能的结果的序号填在横线上)
①一般的平行四边形;②矩形;③菱形;④正方形;⑤梯形
三、解答题:本题共3小题,共25分.
26.已知函数.
(1)求函数的单调递减区间及其图象的对称中心;
(2)已知函数的图象经过先平移后伸缩得到的图象,试写出其变换过程.
27.A B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
B同学的成绩不慎被墨迹污染(,分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差s2=19,求m,n.
28.设函数且是定义域为的奇函数;
(1)若,判断的单调性并求不等式的解集;
(2)若,且,求在上的最小值.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
答案与解析
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.已知集合,,则( )
A. B. C. D.
【答案】D
【解析】由已知可得.
故选:D.
2.己知命题p:,.则命题p的否定是( )
A., B.,
C., D.,
【答案】A
【解析】特称命题的否定是全称命题.
原命题的否定是:,.
故选:A.
3.口袋中共有2个白球2个黑球,从中随机取出两个球,则两个球颜色不同的概率为( )
A. B. C. D.
【答案】A
【解析】设2个白球分别为,2个黑球为,从中随机取出两个球,则所有可能的情况有,,,,,共6种情况,
其中两个球颜色不同的情况有,,,共4种情况,故两个球颜色不同的概率为
故选:A
4.“且”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【解析】充分性: 且,则,充分性成立;必要性: 若,则且,或且,必要性不成立.故“且”是“”的充分而不必要条件.
故选:A.
5.( )
A.1 B. C. D.
【答案】A
【解析】。
故选;A。
6.若一个正方体的体对角线长为a,则这个正方体的全面积为( )
A. B. C. D.
【答案】A
【解析】设正方体的棱长为x,则,即,
所以正方体的全面积为.
故选:A
7.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法抽取一个容量为n的样本,已知从女学生中抽取的人数为80,则n为( )
A.16 B.96 C.192 D.112
【答案】C
【解析】由于采用分层抽样,
每种样本类型中抽取的人数比例为
则
故选:C.
8.已知 ,且 为第四象限角,则 ( )
A. B.
C. D.
【答案】A
【解析】 为第四象限,
,
故选:A
9.已知向量,若,则( )
A. B. C. D.
【答案】D
【解析】因为,,
所以,解得.
故选:D.
10.函数的图象的一个对称轴方程是( )
A. B. C. D.
【答案】C
【解析】对于函数,令,
解得,故函数的对称轴方程为,
令,可知函数的一条对称轴为.
故选:C
11.在中,若,则-定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
【答案】C
【解析】由向量的数量积的运算公式,可得,即,
因为,所以为钝角,所以-定是钝角三角形.
故选:C.
12.设a、b、c表示三条直线,,表示两个平面,下面命题中不正确的是( )
A. B.
C. D.
【答案】D
【解析】A选项:因为,所以垂直平面内的所有直线,又∥,所以平面内的任意直线在平面内都存在直线与之平行,所以垂直平面内的任意直线,,A正确;
B选项:
如图,为直线,为斜足,过作,所以为在平面内的投影,因为,,所以,又,,平面,平面,所以平面,又平面,所以,B正确;
C选项:根据线面平行的判定定理可得C正确;
D选项:不能说明和平面内的直线都垂直,所以D错.
故选;D.
13.函数的图像可能是( )
A. B.
C. D.
【答案】C
14.函数y=的定义域为( )
A.(1,2) B.[1,2)
C.(1,2] D.[1,2]
【答案】A
【解析】由题意得,解得1
15.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数、中位数与平均数分别为( )
A.、、; B.、、;
C.、、; D.、、.
【答案】C
【解析】众数是频率分布直方图中最高矩形的底边中点的横坐标,则众数是,
中位数是把频率分布直方图分成两个面积相等部分的平行于轴的直线的横坐标,
第一个矩形的面积是,第三个矩形的面积是,
故将第二个矩形分成即可,中位数是,
平均数为,
故选:C.
16.若对于任意实数,恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】A
【解析】对于任意实数,不等式恒成立,
当时,,不恒成立,不符合题意;
当时,应满足,即,解得;
综上,实数的取值范围是.
故选:A.
17.甲,乙两人独立地破解同一个谜题,破解出谜题的概率分别为,则谜题被破解的概率为( )
A. B. C. D.1
【答案】C
【解析】设甲,乙两人破解出谜题分别为事件,
则有,则,
谜题被破解的对立事件是甲乙都没有破解谜题,
则.
故选:C.
18.设,则的大小关系为( )
A. B. C. D.
【答案】D
【解析】因为,
,
,
所以.
故选:D.
19.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是( )
A. B.
C. D.
【答案】A
【解析】对A,如图,易得平面平面,但平面与相交,故直线与平面不平行;
对B,如图,为所在棱的中点,根据中位线的性质有,且,,故平行四边形,故,故,故直线与平面平行.
对C,根据中位线与平行四边形的性质,同理可得,直线与平面平行;
对D,根据中位线与平行四边形的性质,同理可得,直线与平面平行;
故选:A
20.若函数是定义在上的偶函数,且在上是增函数,,则不等式的解集为( )
A. B. C. D.
【答案】A
【解析】函数是定义在上的偶函数,可得,
由在,上是增函数,可得在,是减函数,
又(2),可得不等式即为
即有,即,解得,所以解集为.
故:A.
二、填空题:本大题共5小题,每小题3分,共15分.
21.已知z=2+i(其中i为虚数单位),则=______.
【答案】
【解析】因,所以.
故答案为:
22.已知函数,则__________.
【答案】32
【解析】由题意可得:,则
故答案为:32.
23.__________.
【答案】
【解析】.
故答案为:.
24.已知,且,则xy的最大值是___________.
【答案】4
【解析】x>0,y>0,且,则,
解得,当且仅当时取等号,
所以xy的最大值是.
故答案为:4
25.用一个平面去截直三棱柱,交分别于点. 若,则截面的形状可以为________.(把你认为可能的结果的序号填在横线上)
①一般的平行四边形;②矩形;③菱形;④正方形;⑤梯形
【答案】②④⑤
【解析】为直三棱柱,则面面,截面过面、面,则交线,
当不与平行时,此时截得的EH不平行于FG,四边形为梯形;
当时,此时截得的,,
当时,四边形为矩形;当时,四边形为正方形;
故答案为:②④⑤
三、解答题:本题共3小题,共25分.
26.已知函数.
(1)求函数的单调递减区间及其图象的对称中心;
(2)已知函数的图象经过先平移后伸缩得到的图象,试写出其变换过程.
【答案】(1)单调递减区间为,,对称中心为,.
(2)答案见解析
【解析】(1)令,,得,,
因此函数的单调递减区间是,.
令,,得,,因此函数图象的对称中心是,.
(2)
,先将函数的图象向右平移个单位长度,得到的图象,
接着把图象上所有点的纵坐标不变,横坐标伸长为原来的2倍,得到的图象,
最后把图象上所有点的横坐标不变,纵坐标伸长为原来的2倍,得到的图象.
27.A B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
B同学的成绩不慎被墨迹污染(,分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差s2=19,求m,n.
【答案】(1)茎叶图答案见解析,选派B同学参加数学竞赛更好,理由见解析;(2)m=8,n=0.
【解析】(1)A,B两同学参加了8次测验,成绩(单位:分)茎叶图如下:
由茎叶图可知,B同学的平均成绩高于A同学的平均成绩,
所以选派B同学参加数学竞赛更好;
(2)因为,
所以①,
因为,
所以②,
联立①②解得,.
28.设函数且是定义域为的奇函数;
(1)若,判断的单调性并求不等式的解集;
(2)若,且,求在上的最小值.
【答案】(1)增函数,;(2).
【解析】(1)因为函数且是定义域为的奇函数,
可得,从而得,即
当时,函数,
满足,所以,
由,可得且,解得,所以是增函数,
又由,可得,
所以,解得,即不等式的解集是.
(2)由(1)知,,
因为,即,解得,
故,
令,则在上是增函数,故,
即,
此时函数的对称轴为,且开口向上,
所以当,函数取得最小值,最小值为,
即函数的最小值为.
同课章节目录
