山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷5(含答案)
文档属性
| 名称 | 山东省2022年冬季普通高中学业水平合格考试数学预测压轴试卷5(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 08:37:31 | ||
图片预览




文档简介
山东省2022年冬季普通高中学业水平合格考试
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.
A. B. C. D.
2.函数的最小正周期为
A. B. C. D.
3.设集合,集合,3,,则
A., B.,2,3, C.,1,2,3, D.,1,
4.“(2x﹣1)x=0”是“x=0”的( )
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.既不是充分条件,也不是必要条件
D.既是充分条件,也是必要条件
5.已知袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,则下列判断不正确的是
A.事件“都是红色卡片”是随机事件
B.事件“都是蓝色卡片”是不可能事件
C.事件“至少有一张蓝色卡片”是必然事件
D.事件“有1张红色卡片和2张蓝色卡片”是随机事件
6.在平行四边形中,
A. B. C. D.
7.函数的定义域是
A., B.,,
C. D.,
8.若,,,且,则下列不等式一定成立的是
A. B. C. D.
9.已知幂函数的图象过点,则(3)
A.9 B.3 C. D.
10.一个盒子中装有3个红球和1个白球(这些球除颜色外其余均相同),从中任取2个球,设事件 “恰有一个红球”,则(A)
A. B. C. D.
11.如果,那么等于
A. B. C. D.
12.设函数,则(3)等于
A. B.1 C.2 D.0
13.已知直线,,平面满足,,则直线与直线的位置关系是
A.平行 B.相交或异面 C.异面 D.平行或异面
14.下列图形是函数的图象的是
A. B.
C. D.
15.射击运动员甲、乙分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9.两人中恰有一人射中目标的概率是
A.0.06 B.0.16 C.0.26 D.0.72
16.已知向量,不共线,若,,,则
A.,,三点共线 B.,,三点共线
C.,,三点共线 D.,,三点共线
17.若函数f(x)=(m﹣1)x+1在R上是增函数,则f(m)与f(1)的大小关系是( )
A.f(m)<f(1) B.f(m)>f(1) C.f(m)≤f(1) D.f(m)≥f(1)
18.若命题“,”是假命题,则实数的取值范围为
A.,, B.,
C., D.,,
19.将函数的图象上所有的点的横坐标缩短到原来的(纵坐标不变),再将得到的图象向右平移个单位,得到的图象对应的函数解析式为
A. B.
C. D.
20.圆柱内有一个球,该球与圆柱的上、下底面及母线均相切,已知圆柱的体积为,则球的体积为
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
21.(A),(B),且,则 .
22.已知圆锥底面半径为1,高为,则该圆锥的侧面积为 .
23.已知向量=(0,﹣1),||=4,=2,则与的夹角为 .
24.某单位有老年人28人,中年人52人,青年人80人,为调查身体健康状况,需要从中抽取一个容量为40的样本,用分层抽样方法应分别从老年人、中年人、青年人中各抽取 人、 人、 人.
25.已知函数在内有零点,则实数的取值范围是
三、解答题:本题共3小题,共25分.
26.已知某校高一年级全体学生的期末数学成绩全部介于65分到145分之间(满分150分),为了解该年级学生的数学成绩情况,现从该年级的1000名学生中随机抽取50名学生的数学成绩,并分成八组:第一组,,第二组,,第八组,,得到如图所示的频率分布直方图.
(1)求第七组的频率,并补全频率分布直方图;
(2)求这50名学生数学成绩的平均分;
(3)记数学成绩在120分以上为“优秀”,试估计该年级数学成绩为“优秀”的学生的人数.
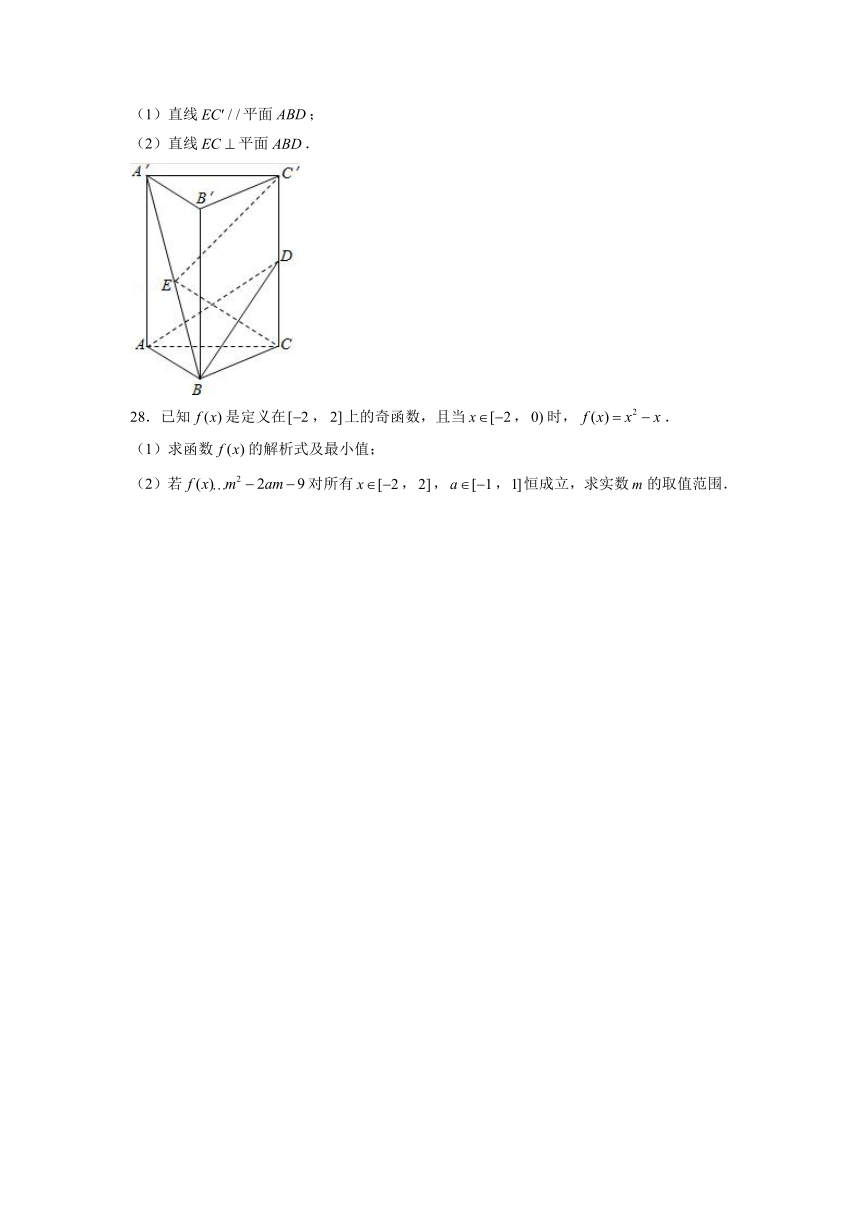
27.如图,在正三棱柱中,、分别为,中点,.求证:
(1)直线平面;
(2)直线平面.
28.已知是定义在,上的奇函数,且当,时,.
(1)求函数的解析式及最小值;
(2)若对所有,,,恒成立,求实数的取值范围.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
参考答案与试题解析
一.选择题(共20小题)
1.
A. B. C. D.
【解析】.
故选:.
2.函数的最小正周期为
A. B. C. D.
【解析】由三角函数的周期公式得,
故选:.
3.设集合,集合,3,,则
A., B.,2,3, C.,1,2,3, D.,1,
【解析】,2,,,3,,
,2,3,.
故选:.
4.“(2x﹣1)x=0”是“x=0”的( )
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.既不是充分条件,也不是必要条件
D.既是充分条件,也是必要条件
【解析】(2x﹣1)x=0等价于x=或x=0,
所以“(2x﹣1)x=0”是“x=0”的必要不充分条件.
故选:B.
5.已知袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,则下列判断不正确的是
A.事件“都是红色卡片”是随机事件
B.事件“都是蓝色卡片”是不可能事件
C.事件“至少有一张蓝色卡片”是必然事件
D.事件“有1张红色卡片和2张蓝色卡片”是随机事件
【解析】袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,
在中,事件“都是红色卡片”是随机事件,故正确;
在中,事件“都是蓝色卡片”是不可能事件,故正确;
在中,事件“至少有一张蓝色卡片”是随机事件,故错误;
在中,事件“有1张红色卡片和2张蓝色卡片”是随机事件,故正确.
故选:.
6.在平行四边形中,
A. B. C. D.
【解析】在平行四边形中,
.
故选:.
7.函数的定义域是
A., B.,,
C. D.,
【解析】由题意可得,
解得或.
即函数的定义域为,,,
故选:.
8.若,,,且,则下列不等式一定成立的是
A. B. C. D.
【解析】由,不一定成立;对于,时不成立;取,时,不成立.
由函数在上单调递增,可知:正确.
故选:.
9.已知幂函数的图象过点,则(3)
A.9 B.3 C. D.
【解析】设,
幂函数的图象过点,
,,
,
则(3),
故选:.
10.一个盒子中装有3个红球和1个白球(这些球除颜色外其余均相同),从中任取2个球,设事件 “恰有一个红球”,则(A)
A. B. C. D.
【解析】一个盒子中装有3个红球和1个白球(这些球除颜色外其余均相同),从中任取2个球,共有种取法,
事件 “恰有一个红球”的方法数为种,
因此(A),
故选:.
11.如果,那么等于
A. B. C. D.
【解析】因为,
所以.
故选:.
12.设函数,则(3)等于
A. B.1 C.2 D.0
【解析】函数,
(3),
(3)(2),
故选:.
13.已知直线,,平面满足,,则直线与直线的位置关系是
A.平行 B.相交或异面 C.异面 D.平行或异面
【解析】直线,,平面满足,,
直线与直线的位置关系可能异面,可能平行,不能相交,
故选:.
14.下列图形是函数的图象的是
A. B.
C. D.
【解析】令,则,函数是奇函数
时,,
函数的图象在第一、三象限,且为单调增函数
故选:.
15.射击运动员甲、乙分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9.两人中恰有一人射中目标的概率是
A.0.06 B.0.16 C.0.26 D.0.72
【解析】由题意甲中乙不中情况的概率为;
乙中甲不中情况的概率为,
所以两人中恰有一人射中目标的概率是:,
故选:.
16.已知向量,不共线,若,,,则
A.,,三点共线 B.,,三点共线
C.,,三点共线 D.,,三点共线
【解析】向量,不共线,
,,,
,
,
,,三点共线.
故选:.
17.若函数f(x)=(m﹣1)x+1在R上是增函数,则f(m)与f(1)的大小关系是( )
A.f(m)<f(1) B.f(m)>f(1) C.f(m)≤f(1) D.f(m)≥f(1)
【解析】∵函数f(x)=(m﹣1)x+1在R上是增函数,
∴m﹣1>0,解得m>1,
∴f(m)>f(1).
故选:B.
18.若命题“,”是假命题,则实数的取值范围为
A.,, B.,
C., D.,,
【解析】,是假命题,
△
或,
实数的取值范围为,,,
故选:.
19.将函数的图象上所有的点的横坐标缩短到原来的(纵坐标不变),再将得到的图象向右平移个单位,得到的图象对应的函数解析式为
A. B.
C. D.
【解析】将函数的图象上所有的点的横坐标缩短到原来的(纵坐标不变),可得的图象;
再将得到的图象向右平移个单位,得到的图象对应的函数解析式为,
故选:.
20.圆柱内有一个球,该球与圆柱的上、下底面及母线均相切,已知圆柱的体积为,则球的体积为
A. B. C. D.
【解析】设圆柱的内切球的半径为,则圆柱的底面圆的半径为,高为,
圆柱的体积为,,
圆柱的内切球的体积为,
故选:.
二.填空题(共5小题)
21.(A),(B),且,则 0.3 .
【解析】根据题意,因为,
所以,(B).
22.已知圆锥底面半径为1,高为,则该圆锥的侧面积为 .
【解析】由已知可得,,则圆锥的母线长.
圆锥的侧面积.
故答案为:.
23.已知向量=(0,﹣1),||=4,=2,则与的夹角为 .
【解析】根据题意,设与的夹角为θ,
向量=(0,﹣1),则||=1,
故cosθ===,
又由0≤θ≤π,则θ=,
故答案为:.
24.某单位有老年人28人,中年人52人,青年人80人,为调查身体健康状况,需要从中抽取一个容量为40的样本,用分层抽样方法应分别从老年人、中年人、青年人中各抽取 7 人、 人、 人.
【解析】由题意知:
老年人数为:;
中年人数为:,
青年人数为:.
故答案为:7;13;20.
25.已知函数在内有零点,则实数的取值范围是
【解析】分类讨论:
①当在内有一个零点时,
由△,得或,此时函数的零点为或1,不合题意,
由零点存在性定理可得(1),即,解得,
②当在内有两个零点时,则,解得,
综上,,即实数的取值范围为,
故答案为:.
三.解答题(共3小题)
26.已知某校高一年级全体学生的期末数学成绩全部介于65分到145分之间(满分150分),为了解该年级学生的数学成绩情况,现从该年级的1000名学生中随机抽取50名学生的数学成绩,并分成八组:第一组,,第二组,,第八组,,得到如图所示的频率分布直方图.
(1)求第七组的频率,并补全频率分布直方图;
(2)求这50名学生数学成绩的平均分;
(3)记数学成绩在120分以上为“优秀”,试估计该年级数学成绩为“优秀”的学生的人数.
【解析】由题意得,
.
所以第七组的频率是0.08.
补全图形得如图:
(2).
所以这50名学生的数学成绩的平均分为102.
(3)由频率分布直方图可知数学成绩为“优秀”的频率为
,由样本估计总体:.
所以得该年级“优秀”的学生大约有150人.
27.如图,在正三棱柱中,、分别为,中点,.求证:
(1)直线平面;
(2)直线平面.
【解答】证明:(1)取中点,连接、.
、为,中点,平行且等于
又平行且等于
平行且等于,
四边形为平行四边形,
又面,面,
面(6分)
(2)连接、
三棱柱为正三棱柱,
面,
面
,面,
,
,
四边形为正方形,
又,
、是平面内的相交直线,面
面,
、是平面内的相交直线,
直线平面(14分)
28.已知是定义在,上的奇函数,且当,时,.
(1)求函数的解析式及最小值;
(2)若对所有,,,恒成立,求实数的取值范围.
【解析】(1)因为函数为定义域上的奇函数,所以,
当,时,,,所以,
因为是奇函数,所以,
所以,
所以;
作出在区间,上的图象,如图:
可得函数在,上为减函数,所以的最小值为(2),
(2)要使对所有,,,恒成立,
即对所有,恒成立,
令(a)
,,,则,
可得:,,
所以实数的取值范围是,.
数学试卷
一、选择题(本大题共20题,每小题3分,共计60分。每小题列出的四个选项中只有一项是最符合题目要求的)
1.
A. B. C. D.
2.函数的最小正周期为
A. B. C. D.
3.设集合,集合,3,,则
A., B.,2,3, C.,1,2,3, D.,1,
4.“(2x﹣1)x=0”是“x=0”的( )
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.既不是充分条件,也不是必要条件
D.既是充分条件,也是必要条件
5.已知袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,则下列判断不正确的是
A.事件“都是红色卡片”是随机事件
B.事件“都是蓝色卡片”是不可能事件
C.事件“至少有一张蓝色卡片”是必然事件
D.事件“有1张红色卡片和2张蓝色卡片”是随机事件
6.在平行四边形中,
A. B. C. D.
7.函数的定义域是
A., B.,,
C. D.,
8.若,,,且,则下列不等式一定成立的是
A. B. C. D.
9.已知幂函数的图象过点,则(3)
A.9 B.3 C. D.
10.一个盒子中装有3个红球和1个白球(这些球除颜色外其余均相同),从中任取2个球,设事件 “恰有一个红球”,则(A)
A. B. C. D.
11.如果,那么等于
A. B. C. D.
12.设函数,则(3)等于
A. B.1 C.2 D.0
13.已知直线,,平面满足,,则直线与直线的位置关系是
A.平行 B.相交或异面 C.异面 D.平行或异面
14.下列图形是函数的图象的是
A. B.
C. D.
15.射击运动员甲、乙分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9.两人中恰有一人射中目标的概率是
A.0.06 B.0.16 C.0.26 D.0.72
16.已知向量,不共线,若,,,则
A.,,三点共线 B.,,三点共线
C.,,三点共线 D.,,三点共线
17.若函数f(x)=(m﹣1)x+1在R上是增函数,则f(m)与f(1)的大小关系是( )
A.f(m)<f(1) B.f(m)>f(1) C.f(m)≤f(1) D.f(m)≥f(1)
18.若命题“,”是假命题,则实数的取值范围为
A.,, B.,
C., D.,,
19.将函数的图象上所有的点的横坐标缩短到原来的(纵坐标不变),再将得到的图象向右平移个单位,得到的图象对应的函数解析式为
A. B.
C. D.
20.圆柱内有一个球,该球与圆柱的上、下底面及母线均相切,已知圆柱的体积为,则球的体积为
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
21.(A),(B),且,则 .
22.已知圆锥底面半径为1,高为,则该圆锥的侧面积为 .
23.已知向量=(0,﹣1),||=4,=2,则与的夹角为 .
24.某单位有老年人28人,中年人52人,青年人80人,为调查身体健康状况,需要从中抽取一个容量为40的样本,用分层抽样方法应分别从老年人、中年人、青年人中各抽取 人、 人、 人.
25.已知函数在内有零点,则实数的取值范围是
三、解答题:本题共3小题,共25分.
26.已知某校高一年级全体学生的期末数学成绩全部介于65分到145分之间(满分150分),为了解该年级学生的数学成绩情况,现从该年级的1000名学生中随机抽取50名学生的数学成绩,并分成八组:第一组,,第二组,,第八组,,得到如图所示的频率分布直方图.
(1)求第七组的频率,并补全频率分布直方图;
(2)求这50名学生数学成绩的平均分;
(3)记数学成绩在120分以上为“优秀”,试估计该年级数学成绩为“优秀”的学生的人数.
27.如图,在正三棱柱中,、分别为,中点,.求证:
(1)直线平面;
(2)直线平面.
28.已知是定义在,上的奇函数,且当,时,.
(1)求函数的解析式及最小值;
(2)若对所有,,,恒成立,求实数的取值范围.
山东省2022年冬季普通高中学业水平合格考试
数学试卷
参考答案与试题解析
一.选择题(共20小题)
1.
A. B. C. D.
【解析】.
故选:.
2.函数的最小正周期为
A. B. C. D.
【解析】由三角函数的周期公式得,
故选:.
3.设集合,集合,3,,则
A., B.,2,3, C.,1,2,3, D.,1,
【解析】,2,,,3,,
,2,3,.
故选:.
4.“(2x﹣1)x=0”是“x=0”的( )
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.既不是充分条件,也不是必要条件
D.既是充分条件,也是必要条件
【解析】(2x﹣1)x=0等价于x=或x=0,
所以“(2x﹣1)x=0”是“x=0”的必要不充分条件.
故选:B.
5.已知袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,则下列判断不正确的是
A.事件“都是红色卡片”是随机事件
B.事件“都是蓝色卡片”是不可能事件
C.事件“至少有一张蓝色卡片”是必然事件
D.事件“有1张红色卡片和2张蓝色卡片”是随机事件
【解析】袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,
在中,事件“都是红色卡片”是随机事件,故正确;
在中,事件“都是蓝色卡片”是不可能事件,故正确;
在中,事件“至少有一张蓝色卡片”是随机事件,故错误;
在中,事件“有1张红色卡片和2张蓝色卡片”是随机事件,故正确.
故选:.
6.在平行四边形中,
A. B. C. D.
【解析】在平行四边形中,
.
故选:.
7.函数的定义域是
A., B.,,
C. D.,
【解析】由题意可得,
解得或.
即函数的定义域为,,,
故选:.
8.若,,,且,则下列不等式一定成立的是
A. B. C. D.
【解析】由,不一定成立;对于,时不成立;取,时,不成立.
由函数在上单调递增,可知:正确.
故选:.
9.已知幂函数的图象过点,则(3)
A.9 B.3 C. D.
【解析】设,
幂函数的图象过点,
,,
,
则(3),
故选:.
10.一个盒子中装有3个红球和1个白球(这些球除颜色外其余均相同),从中任取2个球,设事件 “恰有一个红球”,则(A)
A. B. C. D.
【解析】一个盒子中装有3个红球和1个白球(这些球除颜色外其余均相同),从中任取2个球,共有种取法,
事件 “恰有一个红球”的方法数为种,
因此(A),
故选:.
11.如果,那么等于
A. B. C. D.
【解析】因为,
所以.
故选:.
12.设函数,则(3)等于
A. B.1 C.2 D.0
【解析】函数,
(3),
(3)(2),
故选:.
13.已知直线,,平面满足,,则直线与直线的位置关系是
A.平行 B.相交或异面 C.异面 D.平行或异面
【解析】直线,,平面满足,,
直线与直线的位置关系可能异面,可能平行,不能相交,
故选:.
14.下列图形是函数的图象的是
A. B.
C. D.
【解析】令,则,函数是奇函数
时,,
函数的图象在第一、三象限,且为单调增函数
故选:.
15.射击运动员甲、乙分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9.两人中恰有一人射中目标的概率是
A.0.06 B.0.16 C.0.26 D.0.72
【解析】由题意甲中乙不中情况的概率为;
乙中甲不中情况的概率为,
所以两人中恰有一人射中目标的概率是:,
故选:.
16.已知向量,不共线,若,,,则
A.,,三点共线 B.,,三点共线
C.,,三点共线 D.,,三点共线
【解析】向量,不共线,
,,,
,
,
,,三点共线.
故选:.
17.若函数f(x)=(m﹣1)x+1在R上是增函数,则f(m)与f(1)的大小关系是( )
A.f(m)<f(1) B.f(m)>f(1) C.f(m)≤f(1) D.f(m)≥f(1)
【解析】∵函数f(x)=(m﹣1)x+1在R上是增函数,
∴m﹣1>0,解得m>1,
∴f(m)>f(1).
故选:B.
18.若命题“,”是假命题,则实数的取值范围为
A.,, B.,
C., D.,,
【解析】,是假命题,
△
或,
实数的取值范围为,,,
故选:.
19.将函数的图象上所有的点的横坐标缩短到原来的(纵坐标不变),再将得到的图象向右平移个单位,得到的图象对应的函数解析式为
A. B.
C. D.
【解析】将函数的图象上所有的点的横坐标缩短到原来的(纵坐标不变),可得的图象;
再将得到的图象向右平移个单位,得到的图象对应的函数解析式为,
故选:.
20.圆柱内有一个球,该球与圆柱的上、下底面及母线均相切,已知圆柱的体积为,则球的体积为
A. B. C. D.
【解析】设圆柱的内切球的半径为,则圆柱的底面圆的半径为,高为,
圆柱的体积为,,
圆柱的内切球的体积为,
故选:.
二.填空题(共5小题)
21.(A),(B),且,则 0.3 .
【解析】根据题意,因为,
所以,(B).
22.已知圆锥底面半径为1,高为,则该圆锥的侧面积为 .
【解析】由已知可得,,则圆锥的母线长.
圆锥的侧面积.
故答案为:.
23.已知向量=(0,﹣1),||=4,=2,则与的夹角为 .
【解析】根据题意,设与的夹角为θ,
向量=(0,﹣1),则||=1,
故cosθ===,
又由0≤θ≤π,则θ=,
故答案为:.
24.某单位有老年人28人,中年人52人,青年人80人,为调查身体健康状况,需要从中抽取一个容量为40的样本,用分层抽样方法应分别从老年人、中年人、青年人中各抽取 7 人、 人、 人.
【解析】由题意知:
老年人数为:;
中年人数为:,
青年人数为:.
故答案为:7;13;20.
25.已知函数在内有零点,则实数的取值范围是
【解析】分类讨论:
①当在内有一个零点时,
由△,得或,此时函数的零点为或1,不合题意,
由零点存在性定理可得(1),即,解得,
②当在内有两个零点时,则,解得,
综上,,即实数的取值范围为,
故答案为:.
三.解答题(共3小题)
26.已知某校高一年级全体学生的期末数学成绩全部介于65分到145分之间(满分150分),为了解该年级学生的数学成绩情况,现从该年级的1000名学生中随机抽取50名学生的数学成绩,并分成八组:第一组,,第二组,,第八组,,得到如图所示的频率分布直方图.
(1)求第七组的频率,并补全频率分布直方图;
(2)求这50名学生数学成绩的平均分;
(3)记数学成绩在120分以上为“优秀”,试估计该年级数学成绩为“优秀”的学生的人数.
【解析】由题意得,
.
所以第七组的频率是0.08.
补全图形得如图:
(2).
所以这50名学生的数学成绩的平均分为102.
(3)由频率分布直方图可知数学成绩为“优秀”的频率为
,由样本估计总体:.
所以得该年级“优秀”的学生大约有150人.
27.如图,在正三棱柱中,、分别为,中点,.求证:
(1)直线平面;
(2)直线平面.
【解答】证明:(1)取中点,连接、.
、为,中点,平行且等于
又平行且等于
平行且等于,
四边形为平行四边形,
又面,面,
面(6分)
(2)连接、
三棱柱为正三棱柱,
面,
面
,面,
,
,
四边形为正方形,
又,
、是平面内的相交直线,面
面,
、是平面内的相交直线,
直线平面(14分)
28.已知是定义在,上的奇函数,且当,时,.
(1)求函数的解析式及最小值;
(2)若对所有,,,恒成立,求实数的取值范围.
【解析】(1)因为函数为定义域上的奇函数,所以,
当,时,,,所以,
因为是奇函数,所以,
所以,
所以;
作出在区间,上的图象,如图:
可得函数在,上为减函数,所以的最小值为(2),
(2)要使对所有,,,恒成立,
即对所有,恒成立,
令(a)
,,,则,
可得:,,
所以实数的取值范围是,.
同课章节目录
