分式基本性质(1、2)
图片预览











文档简介
课件33张PPT。16.1.2 分式基本性质(1)复习回顾1、分式的概念: (1) 下列各式中,属于分式的是( )
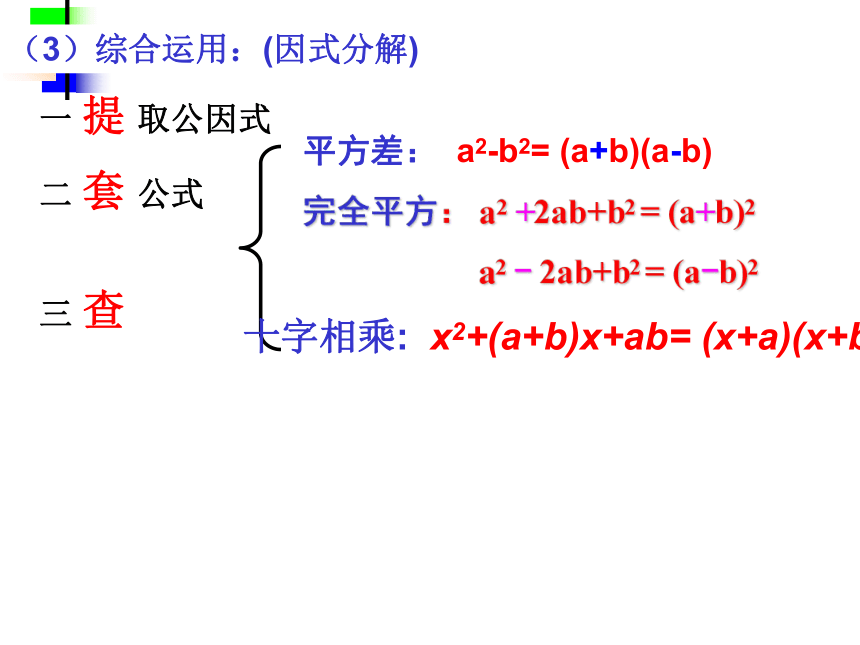
A、 B、 C、 D、B(2)A、B都是整式,则 一定是分式。(3)若B不含字母,则 一定不是分式。×2、分式有意义:3、分式的值为零:(1)x取何值时,分式 有意义;(1)x取何值时,分式 的值为零;(3)综合运用:(因式分解)二 套 公式一 提 取公因式平方差: a2-b2= (a+b)(a-b) 完全平方: a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2 = (a-b)2 十字相乘: x2+(a+b)x+ab= (x+a)(x+b) 三 查新课教学[思考]:下列两式成立吗?为什么?分数的分子与分母同时乘以(或除以)一个不等于0的数,分数的值不变.分数的基本性质:即;对于任意一个分数 有:思考 类比分数的基本性质,你能得到分式的基本性质吗?说说看!类比分数的基本性质,得到:
分式的基本性质:
分式的分子与分母同时乘以(或除以)同一个不等于0的整式 ,分式的值不变.例1? 下列等式的右边是怎样从左边得到的?(1) 由 ,
知 .(2)(2)解: (1)由
知例2:填空:a2+ab2ab-b2x1[小结]:(1)看分母如何变化,想分子如何变化;
(2)看分子如何变化,想分母如何变化; 不改变分式的值,使下列分子与分母都不含“-”号
⑴ ⑵ ⑶例3 [小结]:
分式的符号法则:(1)例4:不改变分式的值,使下列各式的分子与分母中的多项式按x的降幂排列,且首项的系数是正数.当分子或分母是多项式时:先按同一字母次数递减排列,然后,若第一项为负,则多项式添带负号的括号,最后把分子或分母的符号化去。例5:不改变分式的值,把下列各式的分子与分母的各项系数都化为整数。当系数是分数时:分子、分母同乘系数分母的最小公倍数;
当系数是小数时:一般情况下,分子、分母同乘10的倍数。巩固练习1.若把分式 A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍的 和 都扩大两倍,则分式的值( )2.若把分式 中的 和 都扩大3倍,那么分式
的值( ). A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变BA判
断
题:×√×√本节课小结1.分式的基本性质及应用。复习巩固1.若把分式 A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍的 和 都扩大两倍,则分式的值( )2.若把分式 中的 和 都扩大3倍,那么分式
的值( ). A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变BA分数约分把一个分式的分子与分母的公因式约去,叫做分式的约分约分分子、分母系数的最大公约数和分子、分母中相同因式的最低次幂先找出公因式约去公因式化简下列分式 :
(2)(2)例1=ac;=ac , 即分子分母同时约去了整式ab;即分子分母同时约去了整式(x-1) ;= ;把一个分式的分子、分母的公因式约去,这种变形称为分式的约分。约分的依据是什么?分式的基本性质.约简分式(约分)约分的基本步骤:(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.例2分式 化简 的 要求化简下列分式:你对他们两人的做法有何看法? 在小明的化简中,分子和分母已没有公因式,
这样的分式称为最简分式.随堂练习化简下列分式:
(1) (2) 因为分母的最小公倍数是12,所以分数通分1、把分数 通分。解:除12外,以上三个分数还有其它公分母吗?24、48等等也是它们的公分母,但是12是最简公分母! 把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分。 分数通分的方法及步骤是什么?
关键是什么? 先求出几个异分母分数的分母的最小公倍数,作为它们的最简公分母;再把原来的各分数化成用这个公分母做分母的分数。 答:答:关键是找最简公分母2、什么叫分数的通分?
与分数通分类似,
(定义:)把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。 关键是确定几个分式的公分母 通常取各分母所有因式的最高次幂的积作公分母,这样的公分母,叫做最简公分母例1: 求分式的 的最简公分母。 解:公分母是 12系数:对于三个分式的分母中的系数 2,4,6。字母:字母 指数是3,2,1,应取最高次幂 ;字母 应取4次幂;只有第一个分式含有,应取最高次幂1次。关键是字母 ,取出所有出现过的字母,例2 求分式 与 的最简公分母。分析:1、先把这两个分式的分母中的多项式分解因式;解:公分母是2、系数取正数;求几个分式的最简公分母的步骤: (2)取各式的分母中的系数最小公倍数; (3)各分式的分母中所有字母或因式都要取到; (4)相同字母(或因式)的幂取指数最大的; (5)所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母。(1)如果分式的分母能因式分解的,先因式分解; 例3 通分:解:(3)最简公分母是注意书写格式例4 通分 解:所以,最简公分母是故感悟与反思 1、分式的基本性质?
2、分式通分的方法?
3 、分式化简的要求?学习方法指导:
分式化简的目标是“最简”,使用的方法是约分。
为实施约分必须先将分子与分母分解因式。
另外还须注意:
(1)把分子与分母降幂排列;
(2)把最高次方项的负号移到分数线左前方;
(3)把分子与分母的各项系数化为整数。
A、 B、 C、 D、B(2)A、B都是整式,则 一定是分式。(3)若B不含字母,则 一定不是分式。×2、分式有意义:3、分式的值为零:(1)x取何值时,分式 有意义;(1)x取何值时,分式 的值为零;(3)综合运用:(因式分解)二 套 公式一 提 取公因式平方差: a2-b2= (a+b)(a-b) 完全平方: a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2 = (a-b)2 十字相乘: x2+(a+b)x+ab= (x+a)(x+b) 三 查新课教学[思考]:下列两式成立吗?为什么?分数的分子与分母同时乘以(或除以)一个不等于0的数,分数的值不变.分数的基本性质:即;对于任意一个分数 有:思考 类比分数的基本性质,你能得到分式的基本性质吗?说说看!类比分数的基本性质,得到:
分式的基本性质:
分式的分子与分母同时乘以(或除以)同一个不等于0的整式 ,分式的值不变.例1? 下列等式的右边是怎样从左边得到的?(1) 由 ,
知 .(2)(2)解: (1)由
知例2:填空:a2+ab2ab-b2x1[小结]:(1)看分母如何变化,想分子如何变化;
(2)看分子如何变化,想分母如何变化; 不改变分式的值,使下列分子与分母都不含“-”号
⑴ ⑵ ⑶例3 [小结]:
分式的符号法则:(1)例4:不改变分式的值,使下列各式的分子与分母中的多项式按x的降幂排列,且首项的系数是正数.当分子或分母是多项式时:先按同一字母次数递减排列,然后,若第一项为负,则多项式添带负号的括号,最后把分子或分母的符号化去。例5:不改变分式的值,把下列各式的分子与分母的各项系数都化为整数。当系数是分数时:分子、分母同乘系数分母的最小公倍数;
当系数是小数时:一般情况下,分子、分母同乘10的倍数。巩固练习1.若把分式 A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍的 和 都扩大两倍,则分式的值( )2.若把分式 中的 和 都扩大3倍,那么分式
的值( ). A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变BA判
断
题:×√×√本节课小结1.分式的基本性质及应用。复习巩固1.若把分式 A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍的 和 都扩大两倍,则分式的值( )2.若把分式 中的 和 都扩大3倍,那么分式
的值( ). A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变BA分数约分把一个分式的分子与分母的公因式约去,叫做分式的约分约分分子、分母系数的最大公约数和分子、分母中相同因式的最低次幂先找出公因式约去公因式化简下列分式 :
(2)(2)例1=ac;=ac , 即分子分母同时约去了整式ab;即分子分母同时约去了整式(x-1) ;= ;把一个分式的分子、分母的公因式约去,这种变形称为分式的约分。约分的依据是什么?分式的基本性质.约简分式(约分)约分的基本步骤:(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.例2分式 化简 的 要求化简下列分式:你对他们两人的做法有何看法? 在小明的化简中,分子和分母已没有公因式,
这样的分式称为最简分式.随堂练习化简下列分式:
(1) (2) 因为分母的最小公倍数是12,所以分数通分1、把分数 通分。解:除12外,以上三个分数还有其它公分母吗?24、48等等也是它们的公分母,但是12是最简公分母! 把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分。 分数通分的方法及步骤是什么?
关键是什么? 先求出几个异分母分数的分母的最小公倍数,作为它们的最简公分母;再把原来的各分数化成用这个公分母做分母的分数。 答:答:关键是找最简公分母2、什么叫分数的通分?
与分数通分类似,
(定义:)把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。 关键是确定几个分式的公分母 通常取各分母所有因式的最高次幂的积作公分母,这样的公分母,叫做最简公分母例1: 求分式的 的最简公分母。 解:公分母是 12系数:对于三个分式的分母中的系数 2,4,6。字母:字母 指数是3,2,1,应取最高次幂 ;字母 应取4次幂;只有第一个分式含有,应取最高次幂1次。关键是字母 ,取出所有出现过的字母,例2 求分式 与 的最简公分母。分析:1、先把这两个分式的分母中的多项式分解因式;解:公分母是2、系数取正数;求几个分式的最简公分母的步骤: (2)取各式的分母中的系数最小公倍数; (3)各分式的分母中所有字母或因式都要取到; (4)相同字母(或因式)的幂取指数最大的; (5)所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母。(1)如果分式的分母能因式分解的,先因式分解; 例3 通分:解:(3)最简公分母是注意书写格式例4 通分 解:所以,最简公分母是故感悟与反思 1、分式的基本性质?
2、分式通分的方法?
3 、分式化简的要求?学习方法指导:
分式化简的目标是“最简”,使用的方法是约分。
为实施约分必须先将分子与分母分解因式。
另外还须注意:
(1)把分子与分母降幂排列;
(2)把最高次方项的负号移到分数线左前方;
(3)把分子与分母的各项系数化为整数。
