数学人教A版2019必修第一册4.3.1对数的概念(共20张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册4.3.1对数的概念(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 29.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 09:32:30 | ||
图片预览







文档简介
(共20张PPT)
4.3 对数
4.3.1 对数的概念
在4.2.1的问题1中,通过指数幂运算,我们能从y=1.11x中求出经过x年后B地景区的游客人次为2001年的倍数y。反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,...,那么该如何解决?
回顾
?
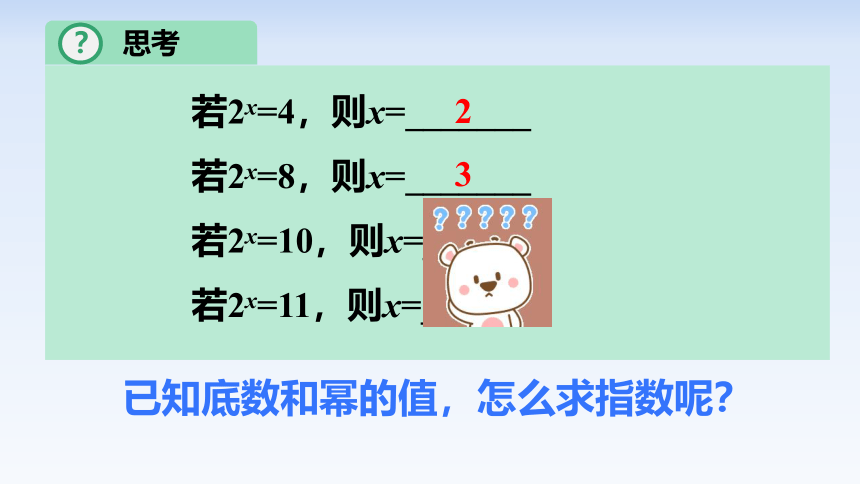
思考
?
若2x=4,则x=_______
若2x=8,则x=_______
若2x=10,则x=_______
若2x=11,则x=_______
2
3
已知底数和幂的值,怎么求指数呢?
PART 1 对数的定义
定义:如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的
对数,记作x=logaN,其中a叫做对数的底数,
N叫做真数
①底数的限制,a>0且a≠1;
②对数的书写格式
注意
定
义
理
解
1.1x=2,那么x可以记作
x=log1.12
读作:以1.1为底2的对数
2x=3,那么x可以记作
x=log23
读作:以2为底3的对数
3x=27,那么x可以记作
x=log327
读作:以3为底27的对数
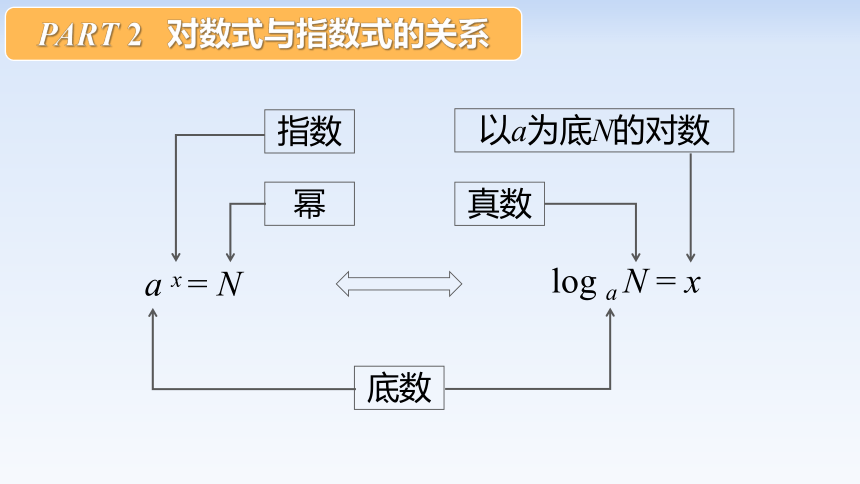
PART 2 对数式与指数式的关系
a x = N
log a N = x
幂
指数
底数
真数
以a为底N的对数
例题探究
例1 把下列指数式化为对数式,对数式化为指数式:
(1)54=625;(2)2-6=;
(3)=5.73;(4)
PART 3 常用对数与自然对数
常用对数:将以10为底的对数叫做常用对数,
并把log10N记做lg N。
自然对数:以无理数e =2.71828…为底的对数,
称为自然对数,并把logeN记做ln N。
例题探究
例1 把下列指数式化为对数式,对数式化为指数式:
(5)lg0.01=-2; (6)ln10=2.303.
解:(5)10-2=0.01; (6)e2.303=10.
例题探究
例2 求下列各式中x的值:
(1)log64x=;(2)logx8=6;
(3)lg100=x; (4)-lne2=x.
指对互化
例题探究
PART 4 对数的基本性质
① 负数和0没有对数
② 1的对数为0 : loga1=0 (a>0,且a≠1)
③ 底数的对数为1 : logaa=1 (a>0,且a≠1)
④ 对数恒等式:
logaax=x (a>0,且a≠1)
(a>0,且a≠1)
题型一 对数的概念判断与求值
例1已知对数式有意义,则a的取值范
围为( )
A.(-1,4) B.(-1,0)∪(0,4)
C.(-4,0)∪(0,1) D.(-4,1)
B
巩固练习1 若log(1+k)(1-k)有意义,则实数k的取值范围是_________
题型一 对数的概念判断与求值
(-1,0)∪(0,1)
题型一 对数的概念判断与求值
例2 求下列各式中的x值:
(1)log5x=3; (2)log2(2x+1)=3;
(3)logx=3; (4)log28x=-3.
题型一 对数的概念判断与求值
例2 求下列各式中的x值:
(1)log5x=3; (2)log2(2x+1)=3;
(3)logx=3; (4)log28x=-3.
题型一 对数的概念判断与求值
巩固练习2求下列各式中x的值:
(1)logx3=; (2)log32x=-;
(3);
(4)log5[log3(log2x)=0.
题型一 对数的概念判断与求值
巩固练习2求下列各式中x的值:
(1)logx3=; (2)log32x=-;
(3);
(4)log5[log3(log2x)]=0.
题型二 指数对数的互化
例3 有以下四个结论,其中正确的是( )
A.lg(lg10)=1 B.lg(lne)=0
C.若e=lnx,则x=e2 D.ln(lg1)=0
B
解析:因为 ln10=lne=1,lg1=0,所以A错误,B正确;
若e=lnx,则x=ee,故C错误;
lg1=0,而ln0没有意义,故D错误.
故选:B
巩固练习2 (多选)下列指数式与对数式互化正确的一组是( )
A.100=1与lg1=0 B.log39=2与=3
C.与log27=- D.log55=1与51=5
题型二 指数对数的互化
ACD
课堂小结
对数的概念
指数与对数的互化
对数的性质
4.3 对数
4.3.1 对数的概念
在4.2.1的问题1中,通过指数幂运算,我们能从y=1.11x中求出经过x年后B地景区的游客人次为2001年的倍数y。反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,...,那么该如何解决?
回顾
?
思考
?
若2x=4,则x=_______
若2x=8,则x=_______
若2x=10,则x=_______
若2x=11,则x=_______
2
3
已知底数和幂的值,怎么求指数呢?
PART 1 对数的定义
定义:如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的
对数,记作x=logaN,其中a叫做对数的底数,
N叫做真数
①底数的限制,a>0且a≠1;
②对数的书写格式
注意
定
义
理
解
1.1x=2,那么x可以记作
x=log1.12
读作:以1.1为底2的对数
2x=3,那么x可以记作
x=log23
读作:以2为底3的对数
3x=27,那么x可以记作
x=log327
读作:以3为底27的对数
PART 2 对数式与指数式的关系
a x = N
log a N = x
幂
指数
底数
真数
以a为底N的对数
例题探究
例1 把下列指数式化为对数式,对数式化为指数式:
(1)54=625;(2)2-6=;
(3)=5.73;(4)
PART 3 常用对数与自然对数
常用对数:将以10为底的对数叫做常用对数,
并把log10N记做lg N。
自然对数:以无理数e =2.71828…为底的对数,
称为自然对数,并把logeN记做ln N。
例题探究
例1 把下列指数式化为对数式,对数式化为指数式:
(5)lg0.01=-2; (6)ln10=2.303.
解:(5)10-2=0.01; (6)e2.303=10.
例题探究
例2 求下列各式中x的值:
(1)log64x=;(2)logx8=6;
(3)lg100=x; (4)-lne2=x.
指对互化
例题探究
PART 4 对数的基本性质
① 负数和0没有对数
② 1的对数为0 : loga1=0 (a>0,且a≠1)
③ 底数的对数为1 : logaa=1 (a>0,且a≠1)
④ 对数恒等式:
logaax=x (a>0,且a≠1)
(a>0,且a≠1)
题型一 对数的概念判断与求值
例1已知对数式有意义,则a的取值范
围为( )
A.(-1,4) B.(-1,0)∪(0,4)
C.(-4,0)∪(0,1) D.(-4,1)
B
巩固练习1 若log(1+k)(1-k)有意义,则实数k的取值范围是_________
题型一 对数的概念判断与求值
(-1,0)∪(0,1)
题型一 对数的概念判断与求值
例2 求下列各式中的x值:
(1)log5x=3; (2)log2(2x+1)=3;
(3)logx=3; (4)log28x=-3.
题型一 对数的概念判断与求值
例2 求下列各式中的x值:
(1)log5x=3; (2)log2(2x+1)=3;
(3)logx=3; (4)log28x=-3.
题型一 对数的概念判断与求值
巩固练习2求下列各式中x的值:
(1)logx3=; (2)log32x=-;
(3);
(4)log5[log3(log2x)=0.
题型一 对数的概念判断与求值
巩固练习2求下列各式中x的值:
(1)logx3=; (2)log32x=-;
(3);
(4)log5[log3(log2x)]=0.
题型二 指数对数的互化
例3 有以下四个结论,其中正确的是( )
A.lg(lg10)=1 B.lg(lne)=0
C.若e=lnx,则x=e2 D.ln(lg1)=0
B
解析:因为 ln10=lne=1,lg1=0,所以A错误,B正确;
若e=lnx,则x=ee,故C错误;
lg1=0,而ln0没有意义,故D错误.
故选:B
巩固练习2 (多选)下列指数式与对数式互化正确的一组是( )
A.100=1与lg1=0 B.log39=2与=3
C.与log27=- D.log55=1与51=5
题型二 指数对数的互化
ACD
课堂小结
对数的概念
指数与对数的互化
对数的性质
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
