分式复习[下学期]
图片预览










文档简介
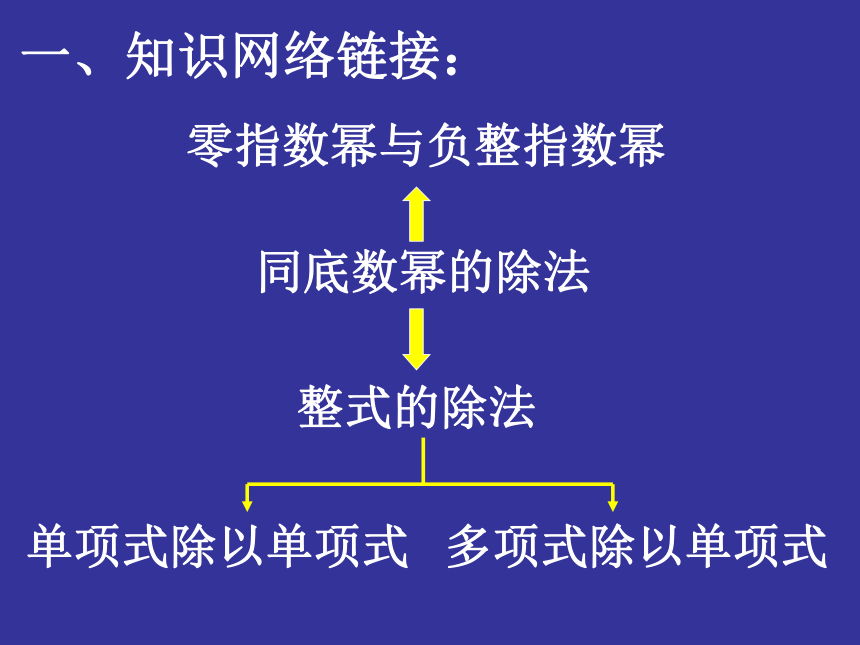
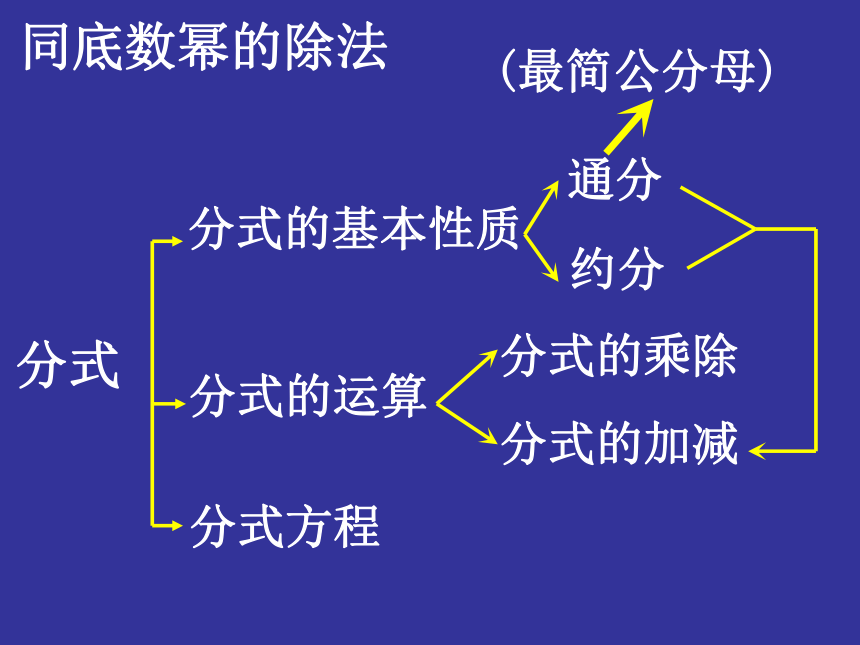
课件33张PPT。分 式一、知识网络链接:零指数幂与负整指数幂同底数幂的除法整式的除法单项式除以单项式 多项式除以单项式同底数幂的除法分式分式的基本性质分式的运算分式方程分式的乘除分式的加减通分约分(最简公分母)二、相关学科链接1、并联电路总电阻R,例1. 已知:两条支路的电阻分别为
欧姆 ,求并联后的总电阻R.解:答:电路中的总电阻为 欧姆.2、杠杆原理例2. 某商店有一架左、右臂长不相等的天平,当顾客欲购质量为2mkg的货物时,营业员先在左盘放上mkg的砝码,右盘放货物,等天平平衡后把货物倒给顾客;然后改为右盘放砝码mkg,左盘放货物,待天平平衡后再倒给顾客,这样,顾客两次共得到货物“2mkg”,你认为这种交易公平吗?试用所学知识加以说明.解:不公平.设左臂长为a,右臂长为b(a≠b)则两次货物实际质量为即这种交易不公平,商店吃亏!三、生活实际链接:例3. 某人以平均每小时2km的速度登山,又以平均每小时6km速度返回,求来回的平均速度.解:设登山的行程为s,则来回总时间为∴平均速度为答:来回的平均速度为3km/t.例4. 某苹果批发商库存有两种苹果,甲种苹果共akg,售价为每千克2元,乙种苹果bkg,售价为每千克4元(a≠b),现在他想把这两种苹果混合在一起卖,你能确定混合的单价是多少吗?若他把定价为每千克3元,你认为合理吗?定价为3元不合理!例5. 甲、乙两人两次同时到同一粮店购买粮食,第一次单价均为x元,第二次单价均为y 元,且x≠y,甲每次购粮100kg,乙每次购粮用去100元.(1)用含x、y的代数式表示:甲两次购粮共需付款___________元,(100x+100y)乙两次共购粮食_______________kg.(2)若甲两次购粮的平均单价为每千克Q1元,乙两次购粮的平均单价为每千克Q2,则Q1=______ ;Q2=______.(3)请你判断甲、乙两人的购粮方式哪一种更合算些?并说明理由.解:∵Q1-Q2=又∵x≠y ∴(x-y)2>0∴ Q1>Q2 ∴乙的购粮方式合算一些.例6. 某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场消费一定金额后,按如下方案获得相应金额的奖券:消费金额a(元)的范围200≤a<400500≤a<700获得奖券的金额(元)400≤a<500700≤a<900…3060100130…根据上述促销方法,顾客在商场内购物可以获得双重优惠则消费金额为450×80%=360元获得的优惠额为450×(1-80%)+30=120元设优惠率=获得的优惠金额÷商品标价如购买标价为450元的商品 (1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?优惠率为330÷1000=33%解:(1)消费金额为1000×80%=800元优惠额为1000×(1-80%)+130=330元①当400≤0.8x<500时,即500≤x<625时解得x=450<500(不合题意,舍去)②当400≤0.8x≤640
时,即500≤x≤800时解得x=750或x=450<500(舍)四、中考预测链接:1、分式的计算与化简求值2、分式有意义与值为零的条件3、科学记数法与零指数幂和负整指数幂4、分式方程及其应用五、试题热身链接:一、选择题1. 下列各式计算中,正确的是( )A、 x10÷(x4÷x2)=x8
B、xn+1÷xn+1=x2
C、 x4n÷x2n×x3n=x3n+2
D、 (xy)5÷xy3=(xy)2ABA、x≠-1
B、x ≠-1且x ≠2
C、x≠2
D、x ≠-1或x ≠2A、扩大2倍B、不变
C、扩大3倍D、扩大4倍ACCAA、-1 B、1
C、-2 D、 37. 下列算式中正确的是( )DCA、m>n
B、m=n
C、 mD、无法确定9. 从一捆粗细均匀的电线上截取1m长的电线,称得它的质量为akg,再称得剩余电线的质量为bkg,则原来这捆电线的总长为( )BDA、2 B、-3
C、 0或-3 D、- 3或3二、填空题11. 用科学记数法表示0.000028为
__________.2.8×10-512. 若93m+1÷32m=27,则m=_____.x≠-2且 x≠-3且x≠-4 5 三、解答题解:原式解:原式=解:将x=2代入方程得解:方程两边同乘以(x-2)得1=x-1-3(x-2)x=2检验得,原方程无解.解:原方程变形为由题设得∴m>1且m≠3时,原方程的解是负数.20.某学校要做一批校服,已知甲做5件与乙做6件所用的时间相同,且两人每天共做55件,求甲、乙两人每天各做多少件?
欧姆 ,求并联后的总电阻R.解:答:电路中的总电阻为 欧姆.2、杠杆原理例2. 某商店有一架左、右臂长不相等的天平,当顾客欲购质量为2mkg的货物时,营业员先在左盘放上mkg的砝码,右盘放货物,等天平平衡后把货物倒给顾客;然后改为右盘放砝码mkg,左盘放货物,待天平平衡后再倒给顾客,这样,顾客两次共得到货物“2mkg”,你认为这种交易公平吗?试用所学知识加以说明.解:不公平.设左臂长为a,右臂长为b(a≠b)则两次货物实际质量为即这种交易不公平,商店吃亏!三、生活实际链接:例3. 某人以平均每小时2km的速度登山,又以平均每小时6km速度返回,求来回的平均速度.解:设登山的行程为s,则来回总时间为∴平均速度为答:来回的平均速度为3km/t.例4. 某苹果批发商库存有两种苹果,甲种苹果共akg,售价为每千克2元,乙种苹果bkg,售价为每千克4元(a≠b),现在他想把这两种苹果混合在一起卖,你能确定混合的单价是多少吗?若他把定价为每千克3元,你认为合理吗?定价为3元不合理!例5. 甲、乙两人两次同时到同一粮店购买粮食,第一次单价均为x元,第二次单价均为y 元,且x≠y,甲每次购粮100kg,乙每次购粮用去100元.(1)用含x、y的代数式表示:甲两次购粮共需付款___________元,(100x+100y)乙两次共购粮食_______________kg.(2)若甲两次购粮的平均单价为每千克Q1元,乙两次购粮的平均单价为每千克Q2,则Q1=______ ;Q2=______.(3)请你判断甲、乙两人的购粮方式哪一种更合算些?并说明理由.解:∵Q1-Q2=又∵x≠y ∴(x-y)2>0∴ Q1>Q2 ∴乙的购粮方式合算一些.例6. 某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场消费一定金额后,按如下方案获得相应金额的奖券:消费金额a(元)的范围200≤a<400500≤a<700获得奖券的金额(元)400≤a<500700≤a<900…3060100130…根据上述促销方法,顾客在商场内购物可以获得双重优惠则消费金额为450×80%=360元获得的优惠额为450×(1-80%)+30=120元设优惠率=获得的优惠金额÷商品标价如购买标价为450元的商品 (1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?优惠率为330÷1000=33%解:(1)消费金额为1000×80%=800元优惠额为1000×(1-80%)+130=330元①当400≤0.8x<500时,即500≤x<625时解得x=450<500(不合题意,舍去)②当400≤0.8x≤640
时,即500≤x≤800时解得x=750或x=450<500(舍)四、中考预测链接:1、分式的计算与化简求值2、分式有意义与值为零的条件3、科学记数法与零指数幂和负整指数幂4、分式方程及其应用五、试题热身链接:一、选择题1. 下列各式计算中,正确的是( )A、 x10÷(x4÷x2)=x8
B、xn+1÷xn+1=x2
C、 x4n÷x2n×x3n=x3n+2
D、 (xy)5÷xy3=(xy)2ABA、x≠-1
B、x ≠-1且x ≠2
C、x≠2
D、x ≠-1或x ≠2A、扩大2倍B、不变
C、扩大3倍D、扩大4倍ACCAA、-1 B、1
C、-2 D、 37. 下列算式中正确的是( )DCA、m>n
B、m=n
C、 m
C、 0或-3 D、- 3或3二、填空题11. 用科学记数法表示0.000028为
__________.2.8×10-512. 若93m+1÷32m=27,则m=_____.x≠-2且 x≠-3且x≠-4 5 三、解答题解:原式解:原式=解:将x=2代入方程得解:方程两边同乘以(x-2)得1=x-1-3(x-2)x=2检验得,原方程无解.解:原方程变形为由题设得∴m>1且m≠3时,原方程的解是负数.20.某学校要做一批校服,已知甲做5件与乙做6件所用的时间相同,且两人每天共做55件,求甲、乙两人每天各做多少件?
