14.1.2 幂的乘方课件

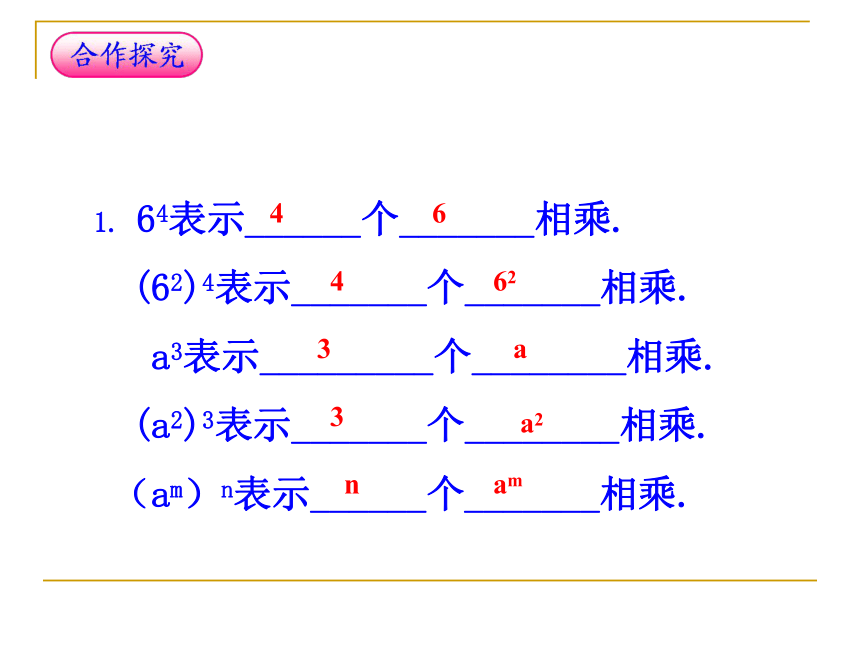
课件17张PPT。14.1.2 幂的乘方（1）（3）（5）（6） （2）（4）1.口述同底数幂的乘法法则am · an = am+n (m、n都是正整数).同底数幂相乘，底数不变，指数相加.2.计算：一个正方体的棱长是10,它的体积是多少?如果它的棱长是102,它的体积又是多少?如果是104呢?103=10 ×10×10(102)3(104)3=106=1012=102×102×102=104×104×104怎样计算?1. 64表示______个_______相乘.
(62)4表示_______个_______相乘.
a3表示_________个________相乘.
(a2)3表示_______个________相乘.
（am）n表示______个_______相乘. 464623a3a2nam(1)(32)3=( )×( )×( )=3( )
(2)(a2)3=( )×( )×( )=a( )
(3)(am)3=( )×( )×( )=a( ) (m为正整数）
根据乘方的意义与同底数幂的乘法填空，看看计算的结果有什么规律？32323266a2a2a2amamam3m(32)3=32 ×3 =36(a2)3=a2 ×3 =a6(am)3=am ×3 =a3m对于任意底数a与任意正整数m,n,（m，n都是正整数）幂的乘方，底数 ，指数 ．不变相乘幂的乘方的运算公式n个am例1:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.解: (1) (103)5=103Χ5 = 1015 ; (2) (a4)4=a4Χ4=a16;
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .例2下面计算是否正确？如有错误请改正。
(1)X3·X3=2X3
(2) X2+X2=X4
(3) a4·a2=a6
(4) (a3)7=a10
(5) (X5)3=X15
(6)-(a3)4=a12√√××××X3·X3=X6X2+X2=2X2
(a3)7=a21-(a3)4=-a12练习
计算：
(103)3; (2) (x3)2;
(3) - ( xm )5 ; (4) (a2 )3? a5;解：例4 计算:
(1) (X2)m+1 (2)[ (X-Y)5]2
(3) –(a2)3·(a4)3 (4)(X2)2·X4+(X2)4
(1) (X2)m+1=X2 (m+1)=X2m+2(2)[ (X-Y)5]2=(X-Y)5×2=(X-Y)10(3) –(a2)3·(a4)3=–a6·a12=–a18(4)(X2)2·X4+(X2)4=X4·X4+X8=X8+X8=2X8
解:想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？乘法乘方不变不变指数
相加指数
相乘幂的乘方的逆运算：
(1)x13·x7=x（ ）=( )5=( )4=( )10；

(2)a2m =( )2 =( )m （m为正整数）.
20x4x5 x2 ama2幂的乘方法则的逆用1.试比较3555,4444,5333的大小.实践与创新解：综合拓展通过计算比较下列各组中两个数的大小:
A 12____21; B 23_____32; C 34_____43;
D 45_____54; E 56_____65;……;
(2) 由题(1)的结果归纳猜想出n n+1和(n+1)n的大小关系是________ ;
(3) 根据上面的结论比较20042005和20052004大小关系是________.
<<>>>再见