华师大版数学八年级上册 13.2 三角形全等的判定(第4课时 A.S.A.)课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级上册 13.2 三角形全等的判定(第4课时 A.S.A.)课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 638.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 12:10:07 | ||
图片预览



文档简介
(共16张PPT)
13.2三角形全等的判定
2.定理:当两个三角形的两条边及其夹角分别对应相等时,两个三角形全等.(S.A.S.)
注意:当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形不一定全等。
两角一边呢
你已经知道的判定三角形全等的方法有几种?
回顾与思考
1.根据三角形全等的定义;
3.定理:当两个三角形的两角及其边分别对应相等时,两个三角形全等.(A.S.A)
4.定理:当两个三角形的两角和其中一角的对边分别对应相等时,两个三角形全等.(A.A.S)
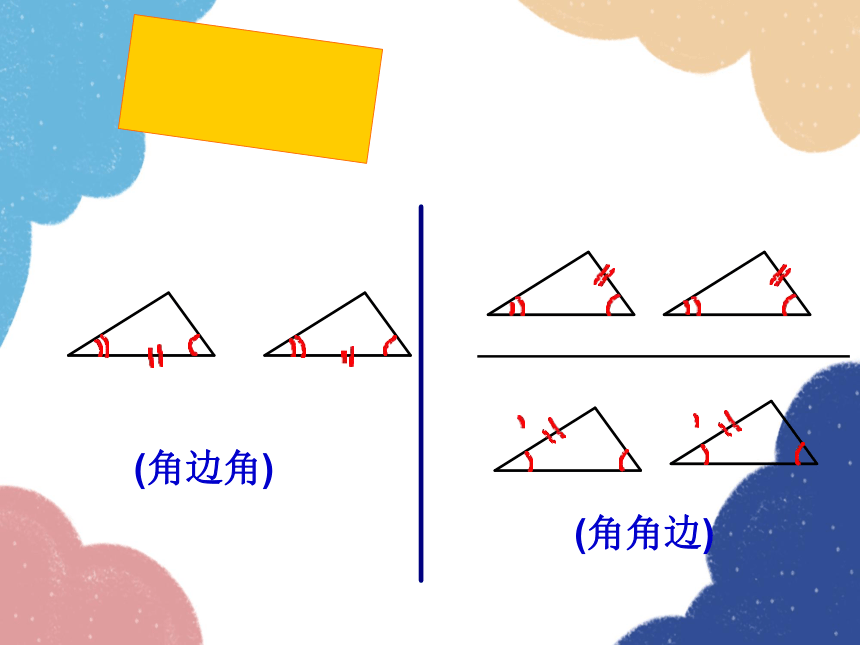
(角边角)
(角角边)
两角一边
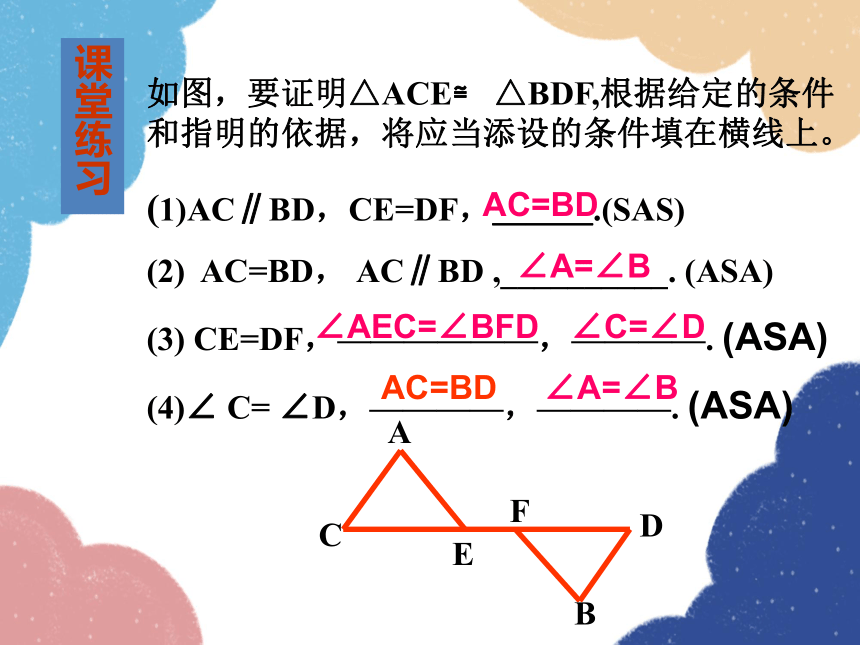
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
(1)AC∥BD,CE=DF,___.(SAS)
(2) AC=BD, AC∥BD ,__________. (ASA)
(3) CE=DF,——————,————. (ASA)
(4)∠ C= ∠D,————,————. (ASA)
C
B
A
E
F
D
课堂练习
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
AC=BD
∠A=∠B
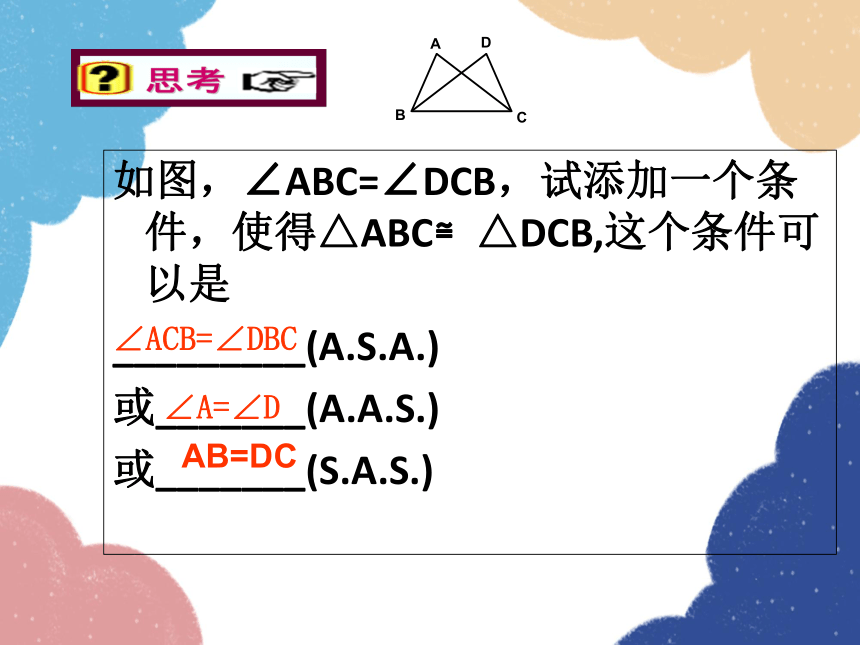
如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
_________(A.S.A.)
或_______(A.A.S.)
或_______(S.A.S.)
∠ACB=∠DBC
∠A=∠D
AB=DC
A
B
C
A′
B′
C′
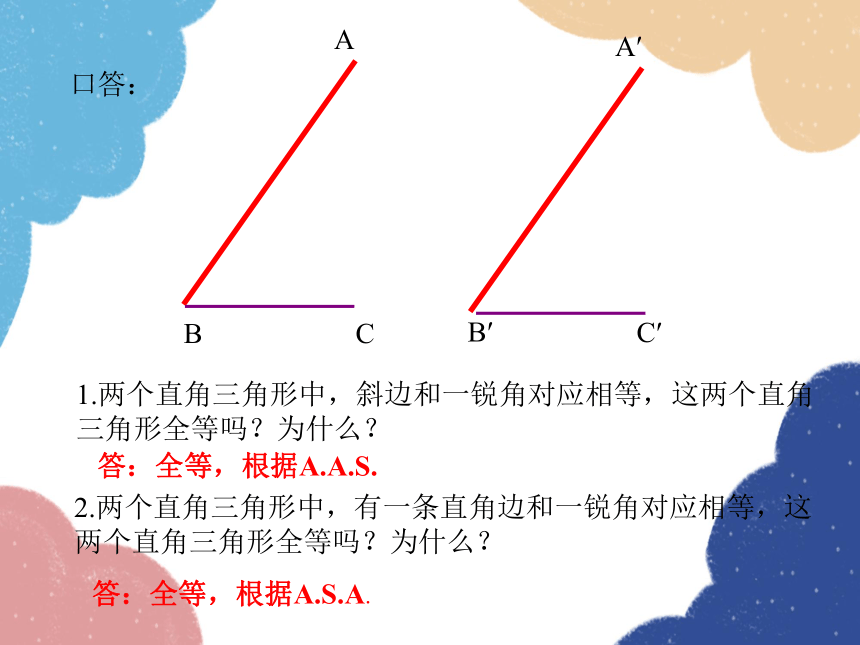
口答:
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?
答:全等,根据A.A.S.
答:全等,根据A.S.A.
根据题目条件,判别下面的两个三角形是否全等,并说明理由.
练一练
例题讲解:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证: △ABE≌△ACD
证明:在△ABE和△ACD中,
∵ ∠B=∠C ,
AB=AC,
∠A=∠A,
∴ △ABE≌△ACD(A.S.A.)
考考你自己
如图,AB⊥BC, AD⊥DC, ∠1=∠2.
求证:AB=AD .
证明:∵ AB⊥BC,AD⊥DC,
∴∠B=∠D=900.
在⊿ABC和⊿ADC中,
∵ ∠B=∠D,
∠1=∠2 ,
AC=AC,
∴ ⊿ABC≌⊿ADC(A.A.S.)
∴AB=AD
如图,填空:
在△AOC和 △BOD中,
∵∠A=∠B(已知)
(已知)
∠C=∠D (已知)
∴△AOC≌△BOD( )
如图,AB//DC,AD//BC,BE⊥AC,DF ⊥ AC垂足为E、F。试说明:BE=DF
探索继续
A
B
C
D
E
F
变形,如图,将上题中的条件“BE⊥AC,DF ⊥ AC”变为“BE //DF”,结论还成立吗?请说明你的理由。
A
B
C
D
E
F
如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.
你也试一试:
若改为:AD、BE分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由.
若改为:AD、BE分别是两腰上的高,△ABD和△BAE全等吗?试说明理由.
已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD。
证明:在△ABD和△ABC中
∵∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
1
2
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复原来三角形的原貌吗?
联系生活
课堂小结
1、通过本节课的学习,你又知道了哪些判定三角形全等的方法?
2、我们已经掌握了哪些判定三角形全等的方法?
13.2三角形全等的判定
2.定理:当两个三角形的两条边及其夹角分别对应相等时,两个三角形全等.(S.A.S.)
注意:当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形不一定全等。
两角一边呢
你已经知道的判定三角形全等的方法有几种?
回顾与思考
1.根据三角形全等的定义;
3.定理:当两个三角形的两角及其边分别对应相等时,两个三角形全等.(A.S.A)
4.定理:当两个三角形的两角和其中一角的对边分别对应相等时,两个三角形全等.(A.A.S)
(角边角)
(角角边)
两角一边
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
(1)AC∥BD,CE=DF,___.(SAS)
(2) AC=BD, AC∥BD ,__________. (ASA)
(3) CE=DF,——————,————. (ASA)
(4)∠ C= ∠D,————,————. (ASA)
C
B
A
E
F
D
课堂练习
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
AC=BD
∠A=∠B
如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
_________(A.S.A.)
或_______(A.A.S.)
或_______(S.A.S.)
∠ACB=∠DBC
∠A=∠D
AB=DC
A
B
C
A′
B′
C′
口答:
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?
答:全等,根据A.A.S.
答:全等,根据A.S.A.
根据题目条件,判别下面的两个三角形是否全等,并说明理由.
练一练
例题讲解:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证: △ABE≌△ACD
证明:在△ABE和△ACD中,
∵ ∠B=∠C ,
AB=AC,
∠A=∠A,
∴ △ABE≌△ACD(A.S.A.)
考考你自己
如图,AB⊥BC, AD⊥DC, ∠1=∠2.
求证:AB=AD .
证明:∵ AB⊥BC,AD⊥DC,
∴∠B=∠D=900.
在⊿ABC和⊿ADC中,
∵ ∠B=∠D,
∠1=∠2 ,
AC=AC,
∴ ⊿ABC≌⊿ADC(A.A.S.)
∴AB=AD
如图,填空:
在△AOC和 △BOD中,
∵∠A=∠B(已知)
(已知)
∠C=∠D (已知)
∴△AOC≌△BOD( )
如图,AB//DC,AD//BC,BE⊥AC,DF ⊥ AC垂足为E、F。试说明:BE=DF
探索继续
A
B
C
D
E
F
变形,如图,将上题中的条件“BE⊥AC,DF ⊥ AC”变为“BE //DF”,结论还成立吗?请说明你的理由。
A
B
C
D
E
F
如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.
你也试一试:
若改为:AD、BE分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由.
若改为:AD、BE分别是两腰上的高,△ABD和△BAE全等吗?试说明理由.
已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD。
证明:在△ABD和△ABC中
∵∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
1
2
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复原来三角形的原貌吗?
联系生活
课堂小结
1、通过本节课的学习,你又知道了哪些判定三角形全等的方法?
2、我们已经掌握了哪些判定三角形全等的方法?
