华师大版数学八年级上册 12.3.2两数和(差)的平方 课件(共19张PPT)
文档属性
| 名称 | 华师大版数学八年级上册 12.3.2两数和(差)的平方 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 655.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
两数和(差)的平方
学习目标
能根据两数和平方公式的特点,正确运用
两数和的平方公式进行计算;通过两数和
的平方公式的推导,来初步体验数学中相互转
化、数形结合的思维方法,了解公式的几何背
景。
公式的结构特征:
左边是
a2 b2;
两个二项式的乘积,
平方差公式
回顾 & 思考
(a+b)(a b)=
即两数和与这两数差的积.
右边是
这两数的平方差.
(a+b) 与(a+2b)2等于多少,而且要用拼图来说明。我到现在还没有结果呢,唉!今天上课又要挨批评了, 怎么办呢 同学们,你们能帮帮我吗
2
昨天,我们数学老师布置了这样一
道题目:
引入
a
2
b
2
ab
ab
a
b
a+b
a+b
a
b
a
2
ab
ab
b
2
(a+b)
2
=
a
2
+
2ab
+
b
2
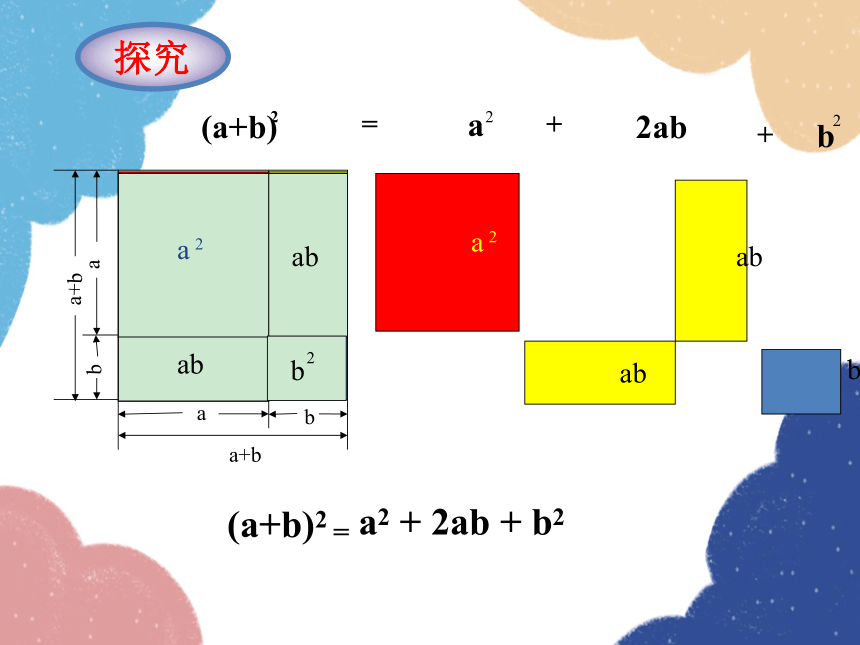
(a+b)2
a2 + 2ab + b2
=
探究
a
a2
b
2
b
ab
ab
b
ab
b
2
b
2
b
2
ab
b
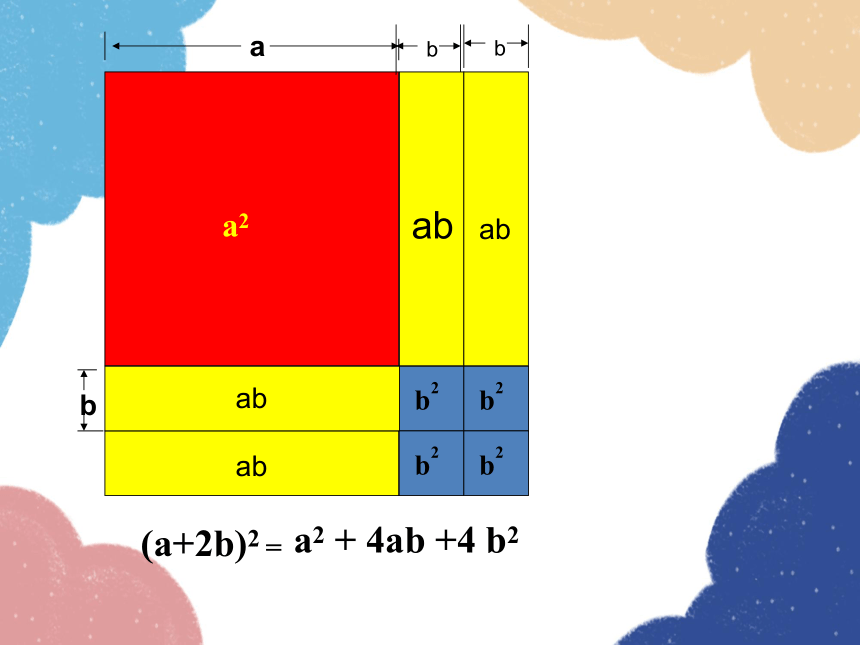
(a+2b)2
a2 + 4ab +4 b2
=
a2
b
2
ab
ab
ab
b
2
b
2
ab
b
2
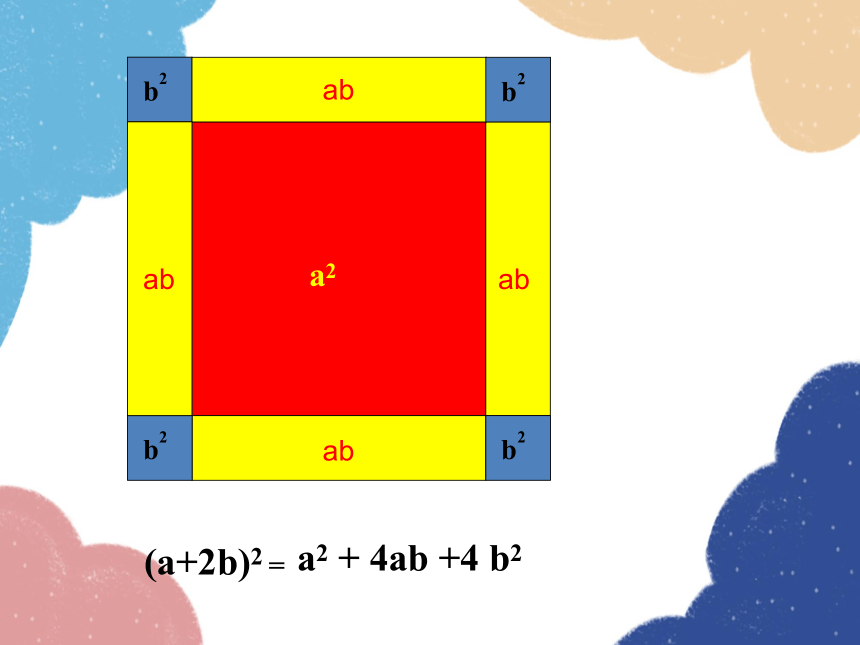
(a+2b)2
a2 + 4ab +4 b2
=
(a+b)2
a2 + 2ab + b2
=
观察公式:它有什么特征呢?
(a+2b)2
a2 + 4ab +4 b2
=
2、我们还可以把公式形象的记为:
这里的“口”和“〇”可以是单项式或多项式。
1、左边是两数和的平方,右边可这样记:
“首平方,尾平方,首尾二倍在中央”
概 括
两数和平方公式的特征:
例题
学一学
例1 利用完全平方公式计算:
(1) (2x+3)2 ; (2) (3m 2n)2
使用完全平方公式与平方差公式的使用一样,
注意
先把要计算的式子与完全平方公式对照,
明确哪个是 a , 哪个是 b.
首项
2x
4x2
2x
的平方,
( )2
加上
2x
第一数
与第二数
+
2x
3
乘积
的2倍,
2
加上
+
尾项
3
的平方.
2
=
+
12x
+
9 ;
解:(1) (2x+3)2
做题时要边念边写:
=
3
(2) (3m 2n)2
=(3m)2 2 (3m) (2n)+(2n)2
=9m2 12mn + 4n2
例2、利用两数和的平方公式
计算:
(1) (a+3b)2 (2) (2x+3y)2
(3) (-2x-y)2 (4) (a-b)2
请说出题中哪部分相当于公式中的 哪部分相当于
解:
(1) (a+3b)2 =
(2) (2x+3y)2
(3) (-2x-y)2
(4) (a-b)2=
研 究 性 学 习
①填空:( )2 =9a2―( )+16b2 ;
②计算:(―a+b)2和(―a―b)2 ;
③与(a+b)2及(a―b)2比较,你发现了什么律?
探索发现:(a+b)2=(―a―b)2 , (a―b)2 = (―a+b)2
解题规律:
当所给的二项式的符号相同时,就用“和”的完全平方式;
当所给的二项式的符号不同时,就用“差”的完全平方式。
做一做
能力提升
1. (1) (2a-5b)2 (2) (2m-n)2
(3) (-3x+y)2
完成后请与同伴交流一下哦!
小组PK现在开始:
能力平台展示
2.请同学们认真学习下面的内容:计算1022
解: 1022
=(100+2)2
=1002+2×100×2+22
=10404
仿照上面的方法计算:
(1)632 (2)99.82
纠 错 练 习
指出下列各式中的错误,并加以改正:
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
解: (1)
第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2 ;
应改为: (2a 1)2= (2a)2 2 2a 1+1;
(2) 少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (2a+1)2= (2a)2+2 2a 1 +1;
(3) 第一数平方未添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: ( a 1)2=( a)2 2 ( a ) 1+12;
你来总结
课堂小结
本题课你有什么收获或感想?你还有什么疑问?
再见
两数和(差)的平方
学习目标
能根据两数和平方公式的特点,正确运用
两数和的平方公式进行计算;通过两数和
的平方公式的推导,来初步体验数学中相互转
化、数形结合的思维方法,了解公式的几何背
景。
公式的结构特征:
左边是
a2 b2;
两个二项式的乘积,
平方差公式
回顾 & 思考
(a+b)(a b)=
即两数和与这两数差的积.
右边是
这两数的平方差.
(a+b) 与(a+2b)2等于多少,而且要用拼图来说明。我到现在还没有结果呢,唉!今天上课又要挨批评了, 怎么办呢 同学们,你们能帮帮我吗
2
昨天,我们数学老师布置了这样一
道题目:
引入
a
2
b
2
ab
ab
a
b
a+b
a+b
a
b
a
2
ab
ab
b
2
(a+b)
2
=
a
2
+
2ab
+
b
2
(a+b)2
a2 + 2ab + b2
=
探究
a
a2
b
2
b
ab
ab
b
ab
b
2
b
2
b
2
ab
b
(a+2b)2
a2 + 4ab +4 b2
=
a2
b
2
ab
ab
ab
b
2
b
2
ab
b
2
(a+2b)2
a2 + 4ab +4 b2
=
(a+b)2
a2 + 2ab + b2
=
观察公式:它有什么特征呢?
(a+2b)2
a2 + 4ab +4 b2
=
2、我们还可以把公式形象的记为:
这里的“口”和“〇”可以是单项式或多项式。
1、左边是两数和的平方,右边可这样记:
“首平方,尾平方,首尾二倍在中央”
概 括
两数和平方公式的特征:
例题
学一学
例1 利用完全平方公式计算:
(1) (2x+3)2 ; (2) (3m 2n)2
使用完全平方公式与平方差公式的使用一样,
注意
先把要计算的式子与完全平方公式对照,
明确哪个是 a , 哪个是 b.
首项
2x
4x2
2x
的平方,
( )2
加上
2x
第一数
与第二数
+
2x
3
乘积
的2倍,
2
加上
+
尾项
3
的平方.
2
=
+
12x
+
9 ;
解:(1) (2x+3)2
做题时要边念边写:
=
3
(2) (3m 2n)2
=(3m)2 2 (3m) (2n)+(2n)2
=9m2 12mn + 4n2
例2、利用两数和的平方公式
计算:
(1) (a+3b)2 (2) (2x+3y)2
(3) (-2x-y)2 (4) (a-b)2
请说出题中哪部分相当于公式中的 哪部分相当于
解:
(1) (a+3b)2 =
(2) (2x+3y)2
(3) (-2x-y)2
(4) (a-b)2=
研 究 性 学 习
①填空:( )2 =9a2―( )+16b2 ;
②计算:(―a+b)2和(―a―b)2 ;
③与(a+b)2及(a―b)2比较,你发现了什么律?
探索发现:(a+b)2=(―a―b)2 , (a―b)2 = (―a+b)2
解题规律:
当所给的二项式的符号相同时,就用“和”的完全平方式;
当所给的二项式的符号不同时,就用“差”的完全平方式。
做一做
能力提升
1. (1) (2a-5b)2 (2) (2m-n)2
(3) (-3x+y)2
完成后请与同伴交流一下哦!
小组PK现在开始:
能力平台展示
2.请同学们认真学习下面的内容:计算1022
解: 1022
=(100+2)2
=1002+2×100×2+22
=10404
仿照上面的方法计算:
(1)632 (2)99.82
纠 错 练 习
指出下列各式中的错误,并加以改正:
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
解: (1)
第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2 ;
应改为: (2a 1)2= (2a)2 2 2a 1+1;
(2) 少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (2a+1)2= (2a)2+2 2a 1 +1;
(3) 第一数平方未添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: ( a 1)2=( a)2 2 ( a ) 1+12;
你来总结
课堂小结
本题课你有什么收获或感想?你还有什么疑问?
再见
