人教版八年级上册 全等三角形 期中复习优质课件(共30张PPT)
文档属性
| 名称 | 人教版八年级上册 全等三角形 期中复习优质课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 587.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 12:27:28 | ||
图片预览



文档简介
(共30张PPT)
《三角形》期中
复习课
一.全等三角形:
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等。
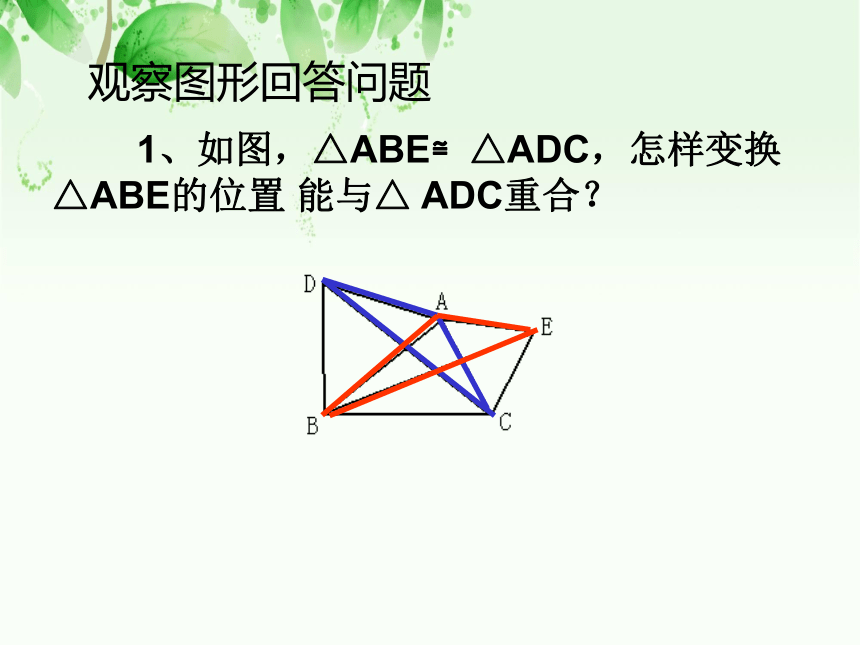
1、如图,△ABE≌△ADC,怎样变换△ABE的位置 能与△ ADC重合?
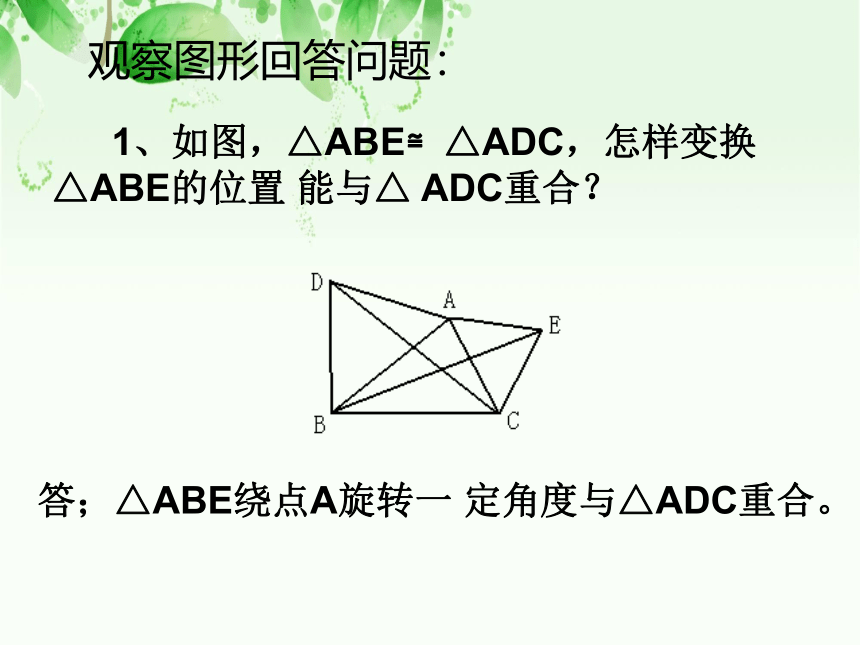
观察图形回答问题
1、如图,△ABE≌△ADC,怎样变换△ABE的位置 能与△ ADC重合?
答;△ABE绕点A旋转一 定角度与△ADC重合。
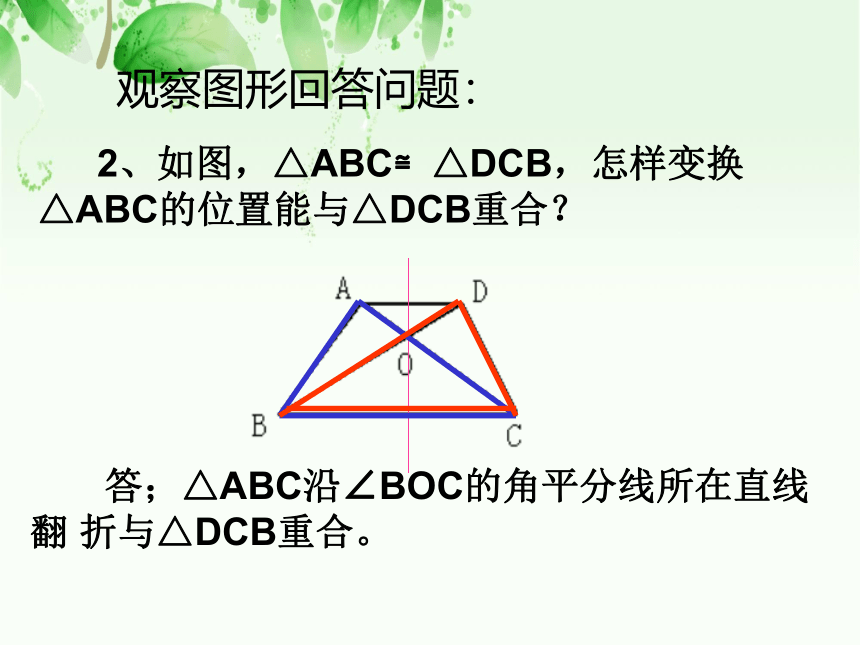
观察图形回答问题:
2、如图,△ABC≌△DCB,怎样变换 △ABC的位置能与△DCB重合?
答;△ABC沿∠BOC的角平分线所在直线翻 折与△DCB重合。
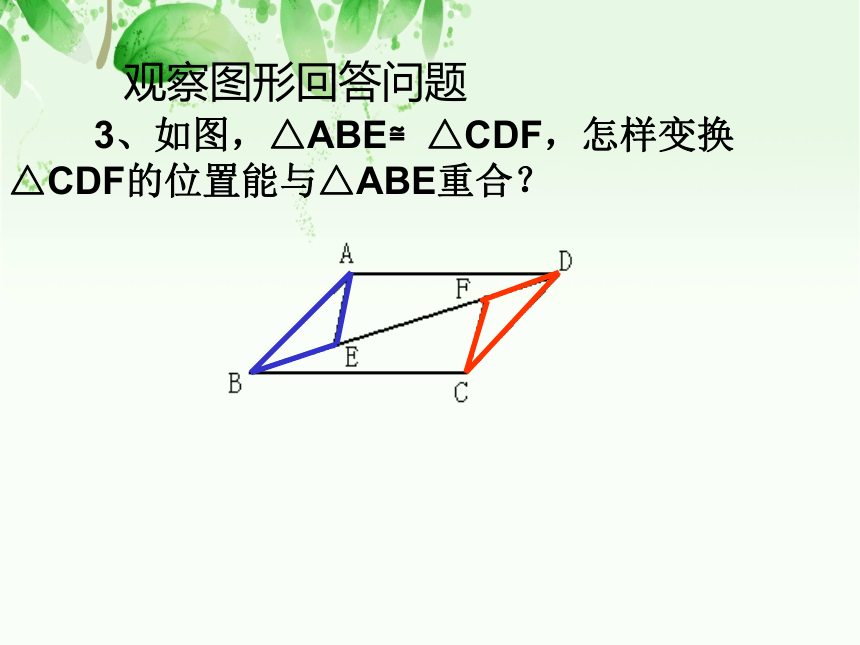
观察图形回答问题:
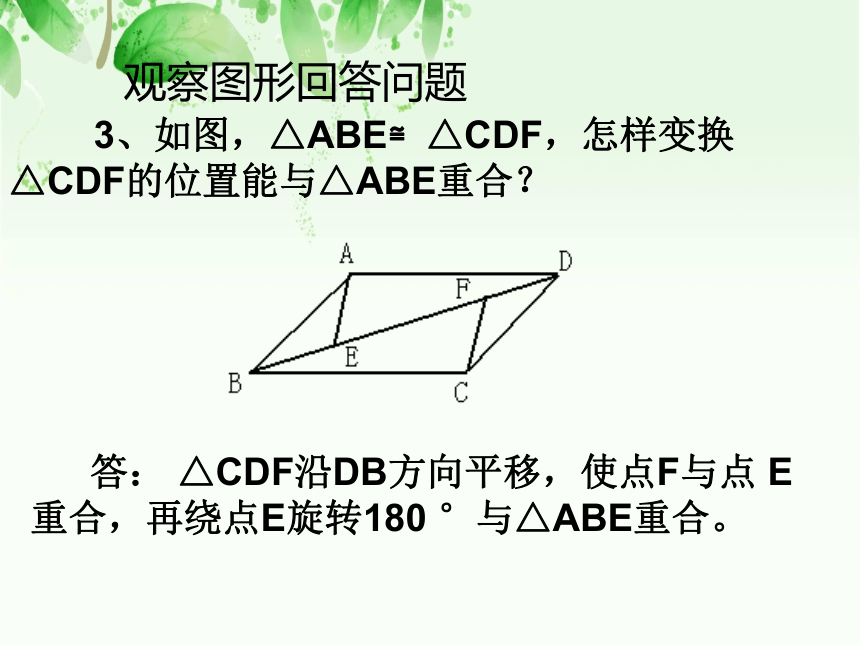
3、如图,△ABE≌△CDF,怎样变换△CDF的位置能与△ABE重合?
观察图形回答问题
3、如图,△ABE≌△CDF,怎样变换△CDF的位置能与△ABE重合?
答: △CDF沿DB方向平移,使点F与点 E重合,再绕点E旋转180 °与△ABE重合。
观察图形回答问题
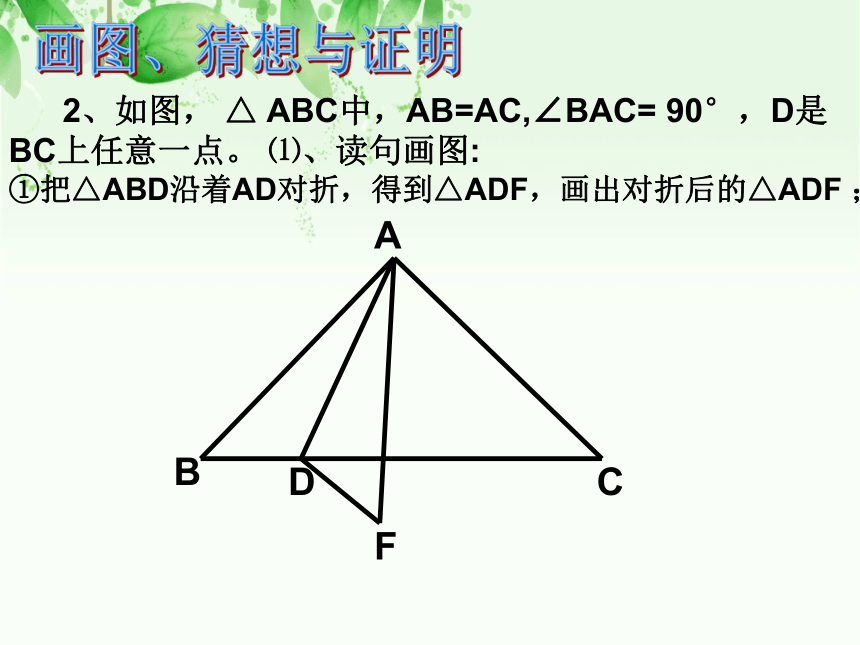
2、△ABC中,AB=AC,∠BAC= 90°,D是BC上任意一点 ⑴、读句画图: ①把△ABD沿着AD对折,得到△ADF,画出对折后的△ADF ;
画图、猜想与证明
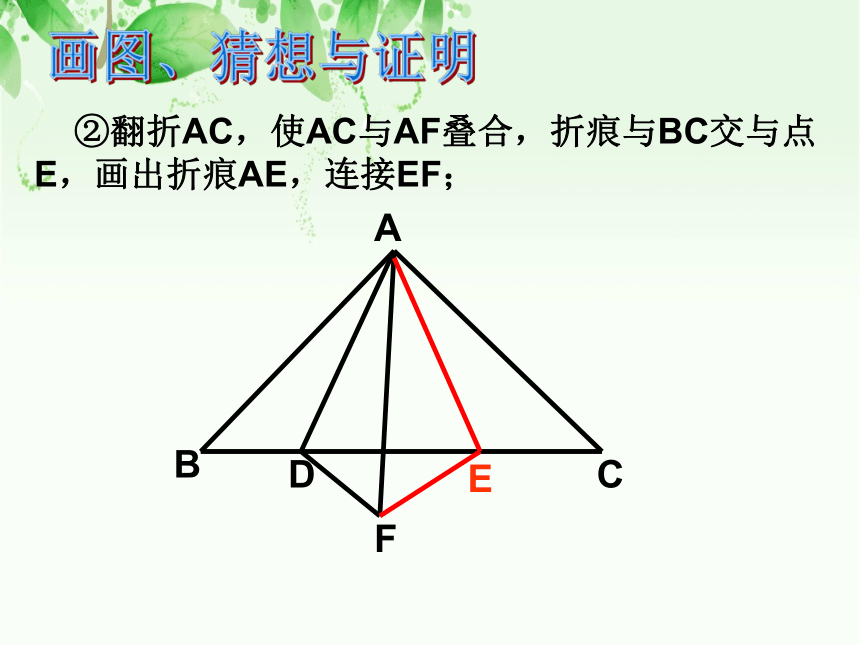
②翻折AC,使AC与AF叠合,折痕与BC交与点E,
画出折痕AE,连接EF;
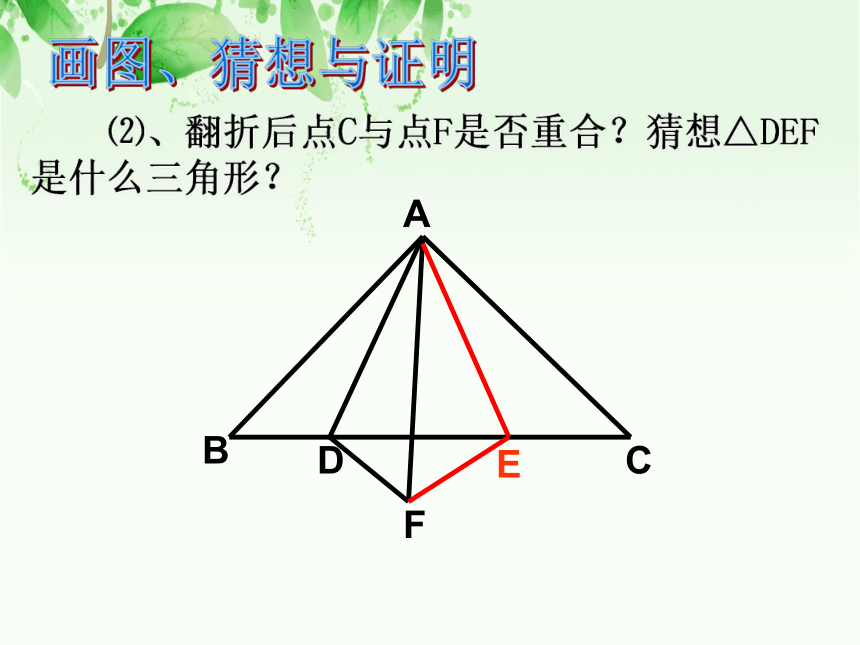
⑵、翻折后点C与点F是否重合?猜想△DEF是什
么三角形?
⑶、证明你的结论。
2、如图, △ ABC中,AB=AC,∠BAC= 90°,D是BC上任意一点。 ⑴、读句画图: ①把△ABD沿着AD对折,得到△ADF,画出对折后的△ADF ;
画图、猜想与证明
A
B
C
D
F
画图、猜想与证明
②翻折AC,使AC与AF叠合,折痕与BC交与点E,画出折痕AE,连接EF;
A
B
C
D
F
E
画图、猜想与证明
⑵、翻折后点C与点F是否重合?猜想△DEF
是什么三角形?
A
B
C
D
F
E
画图、猜想与证明
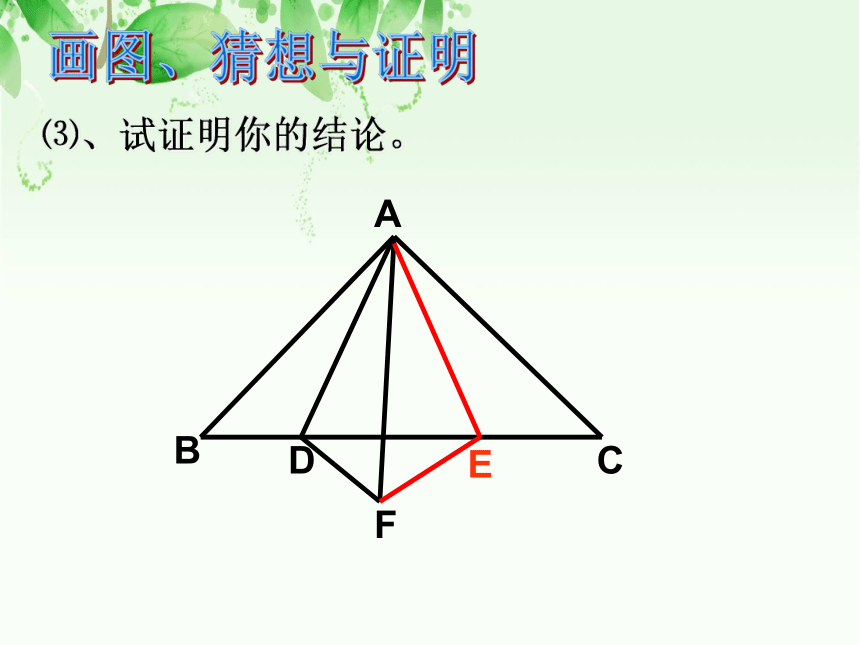
⑶、试证明你的结论。
A
B
C
D
F
E
知识回顾:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
回顾知识点:
边边边:三边对应相等的两个三角形全等(可简写成“SSS”)
边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)
角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)
角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)
斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)
方法指引
证明两个三角形全等的基本思路:
(1):已知两边----
找第三边
(SSS)
找夹角
(SAS)
(2):已知一边一角---
已知一边和它的邻角
找是否有直角
(HL)
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
找一角(AAS)
已知角是直角,找一边(HL)
(3):已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
角的平分线上的点到角的两边的距离相等.
用法:∵ QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上
∴ QD=QE
二.角的平分线:
1.角平分线的性质:
2.角平分线的判定:
1、如图:在△ABC中,∠C =900,AD平分∠ BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE= 。
12
c
A
B
D
E
三.练习:
2.如图, △ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB、BC、CA的距离相等
∵BM是△ABC的角平分线,点P在BM上,
A
B
C
P
M
N
D
E
F
∴PD=PE
(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等
证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
E
D
C
A
B
变式:以上条件不变,将△ABC绕点C旋转一定角度(大于零度而小于六十度),以上的结论海成立吗?
证明:
∵ △ABC和△ECD都是等边三角形
∴ AC=BC DC=EC ∠BCA=∠DCE=60°
∴ ∠BCA+∠ACE=∠DCE+ ∠ACE
即∠BCE=∠DCA
在△ACD和△BCE中
AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
5:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
4
3
2
1
E
D
C
B
A
解:AC=AD
理由:在△EBC和△EBD中
∠1=∠2
∠3=∠4
EB=EB
∴ △EBC≌△EBD (AAS)
∴ BC=BD
在△ABC和△ABD中
AB=AB
∠1=∠2
BC=BD
∴ △ABC≌△ABD (SAS)
∴ AC=AD
练习
6:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
答:
△ABC≌△DEF
证明:
∵ AB∥DE
∴ ∠A=∠D
∵ AF=DC
∴ AF+FC=DC+FC
∴ AC=DF
在△ABC和△DEF中
AC=DF
∠A=∠D
AB=DE
∴ △ABC≌△DEF (SAS)
练习
7:如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知: EG∥AF
求证:
G
F
E
D
C
B
A
高
拓展题
8.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.
求证:BC∥EF
B
C
A
F
E
D
拓展题
9.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由。
A
C
E
B
D
要证明两条线段的和与一条线段相等时常用的两种方法:
1、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
2、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补)
10.如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的延长线于点F,给出下列5个关系式::①AD∥BC,②,DE=EC③∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,另外两个作为结论,构成正确的命题。请用序号写出两个正确的命题:(书写形式:如果……那么……)(1) ;(2) ;
11.如图,在R△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE.
12.已知:如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:△ ADG 为等腰直角三角形。
13.已知:如图21,AD∠BAC,DE⊥AB于E,DF⊥AC于F,DB=DC,
求证:EB=FC
总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
《三角形》期中
复习课
一.全等三角形:
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等。
1、如图,△ABE≌△ADC,怎样变换△ABE的位置 能与△ ADC重合?
观察图形回答问题
1、如图,△ABE≌△ADC,怎样变换△ABE的位置 能与△ ADC重合?
答;△ABE绕点A旋转一 定角度与△ADC重合。
观察图形回答问题:
2、如图,△ABC≌△DCB,怎样变换 △ABC的位置能与△DCB重合?
答;△ABC沿∠BOC的角平分线所在直线翻 折与△DCB重合。
观察图形回答问题:
3、如图,△ABE≌△CDF,怎样变换△CDF的位置能与△ABE重合?
观察图形回答问题
3、如图,△ABE≌△CDF,怎样变换△CDF的位置能与△ABE重合?
答: △CDF沿DB方向平移,使点F与点 E重合,再绕点E旋转180 °与△ABE重合。
观察图形回答问题
2、△ABC中,AB=AC,∠BAC= 90°,D是BC上任意一点 ⑴、读句画图: ①把△ABD沿着AD对折,得到△ADF,画出对折后的△ADF ;
画图、猜想与证明
②翻折AC,使AC与AF叠合,折痕与BC交与点E,
画出折痕AE,连接EF;
⑵、翻折后点C与点F是否重合?猜想△DEF是什
么三角形?
⑶、证明你的结论。
2、如图, △ ABC中,AB=AC,∠BAC= 90°,D是BC上任意一点。 ⑴、读句画图: ①把△ABD沿着AD对折,得到△ADF,画出对折后的△ADF ;
画图、猜想与证明
A
B
C
D
F
画图、猜想与证明
②翻折AC,使AC与AF叠合,折痕与BC交与点E,画出折痕AE,连接EF;
A
B
C
D
F
E
画图、猜想与证明
⑵、翻折后点C与点F是否重合?猜想△DEF
是什么三角形?
A
B
C
D
F
E
画图、猜想与证明
⑶、试证明你的结论。
A
B
C
D
F
E
知识回顾:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
回顾知识点:
边边边:三边对应相等的两个三角形全等(可简写成“SSS”)
边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)
角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)
角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)
斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)
方法指引
证明两个三角形全等的基本思路:
(1):已知两边----
找第三边
(SSS)
找夹角
(SAS)
(2):已知一边一角---
已知一边和它的邻角
找是否有直角
(HL)
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
找一角(AAS)
已知角是直角,找一边(HL)
(3):已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
角的平分线上的点到角的两边的距离相等.
用法:∵ QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上
∴ QD=QE
二.角的平分线:
1.角平分线的性质:
2.角平分线的判定:
1、如图:在△ABC中,∠C =900,AD平分∠ BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE= 。
12
c
A
B
D
E
三.练习:
2.如图, △ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB、BC、CA的距离相等
∵BM是△ABC的角平分线,点P在BM上,
A
B
C
P
M
N
D
E
F
∴PD=PE
(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等
证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
E
D
C
A
B
变式:以上条件不变,将△ABC绕点C旋转一定角度(大于零度而小于六十度),以上的结论海成立吗?
证明:
∵ △ABC和△ECD都是等边三角形
∴ AC=BC DC=EC ∠BCA=∠DCE=60°
∴ ∠BCA+∠ACE=∠DCE+ ∠ACE
即∠BCE=∠DCA
在△ACD和△BCE中
AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
5:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
4
3
2
1
E
D
C
B
A
解:AC=AD
理由:在△EBC和△EBD中
∠1=∠2
∠3=∠4
EB=EB
∴ △EBC≌△EBD (AAS)
∴ BC=BD
在△ABC和△ABD中
AB=AB
∠1=∠2
BC=BD
∴ △ABC≌△ABD (SAS)
∴ AC=AD
练习
6:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
答:
△ABC≌△DEF
证明:
∵ AB∥DE
∴ ∠A=∠D
∵ AF=DC
∴ AF+FC=DC+FC
∴ AC=DF
在△ABC和△DEF中
AC=DF
∠A=∠D
AB=DE
∴ △ABC≌△DEF (SAS)
练习
7:如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知: EG∥AF
求证:
G
F
E
D
C
B
A
高
拓展题
8.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.
求证:BC∥EF
B
C
A
F
E
D
拓展题
9.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由。
A
C
E
B
D
要证明两条线段的和与一条线段相等时常用的两种方法:
1、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
2、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补)
10.如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的延长线于点F,给出下列5个关系式::①AD∥BC,②,DE=EC③∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,另外两个作为结论,构成正确的命题。请用序号写出两个正确的命题:(书写形式:如果……那么……)(1) ;(2) ;
11.如图,在R△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE.
12.已知:如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:△ ADG 为等腰直角三角形。
13.已知:如图21,AD∠BAC,DE⊥AB于E,DF⊥AC于F,DB=DC,
求证:EB=FC
总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
同课章节目录
