人教版数学七年级下册期中复习课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级下册期中复习课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 12:44:26 | ||
图片预览

文档简介
(共16张PPT)
期中复习
人教版 七年级下册
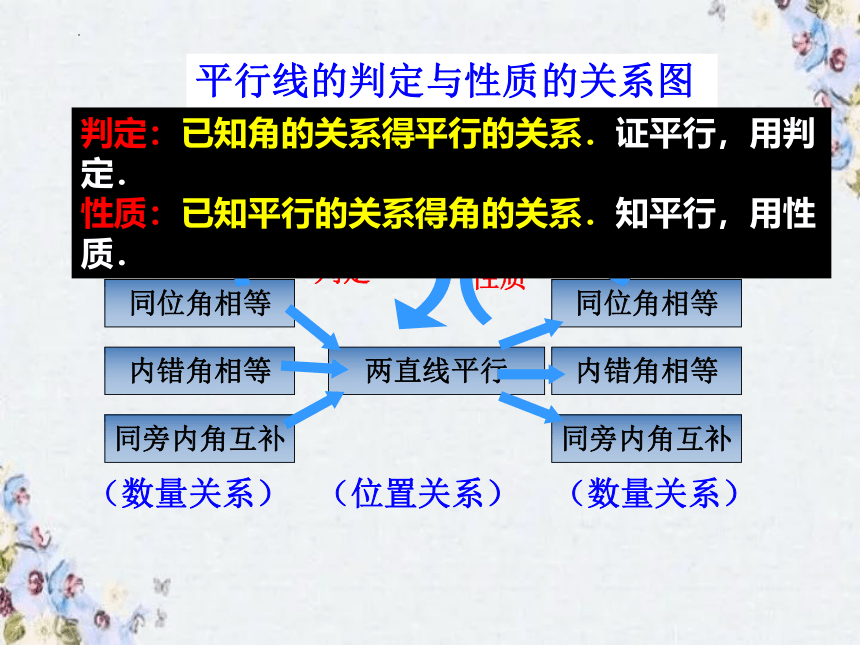
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
(数量关系)
(位置关系)
(数量关系)
平行线的判定与性质的关系图
判定:已知角的关系得平行的关系.证平行,用判定.
性质:已知平行的关系得角的关系.知平行,用性质.
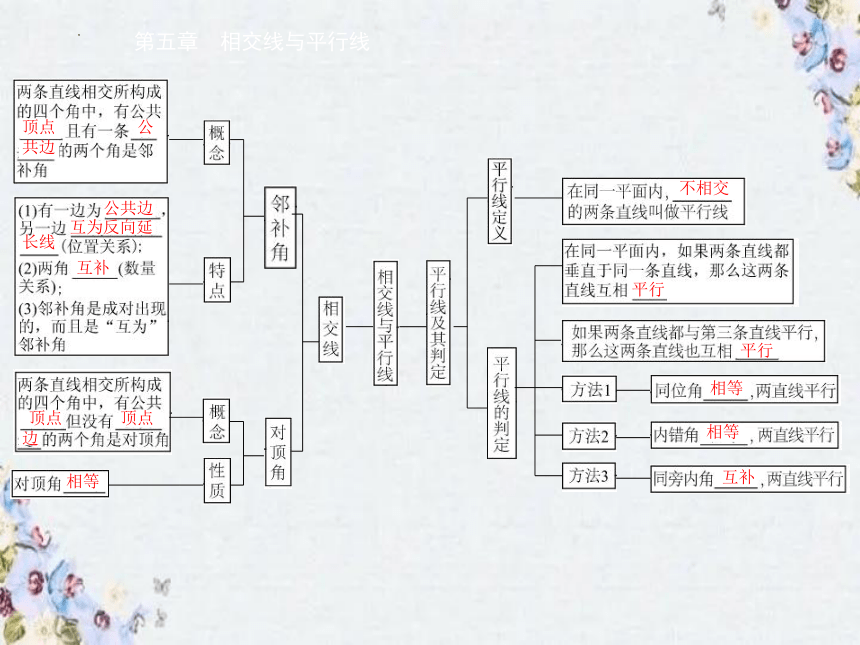
第五章 相交线与平行线
顶点
公
共边
公共边
互为反向延
长线
互补
顶点
顶点
边
相等
不相交
平行
平行
相等
相等
互补
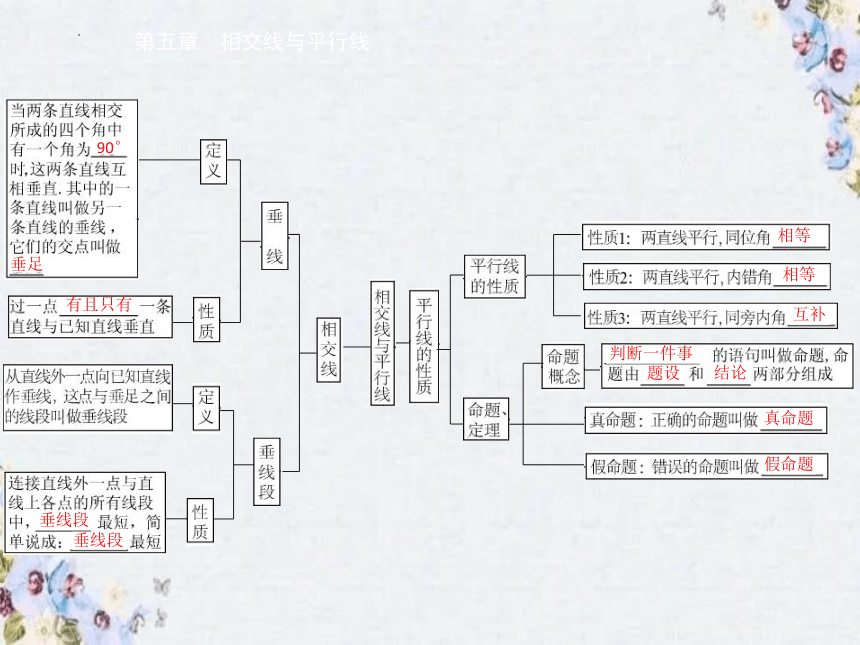
第五章 相交线与平行线
90°
垂足
有且只有
垂线段
垂线段
相等
相等
互补
判断一件事
题设
结论
真命题
假命题
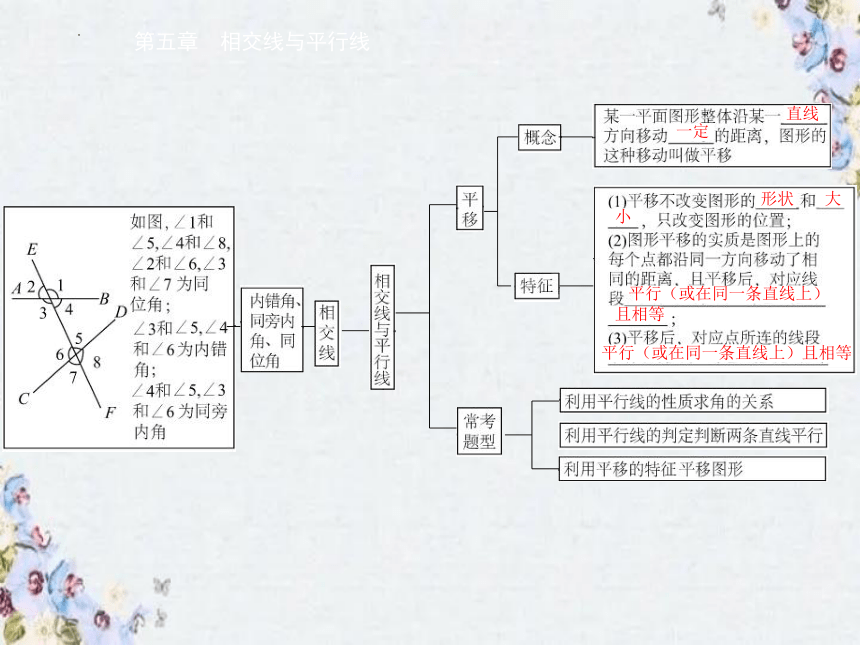
第五章 相交线与平行线
直线
一定
形状
大
小
平行(或在同一条直线上)
且相等
平行(或在同一条直线上)且相等
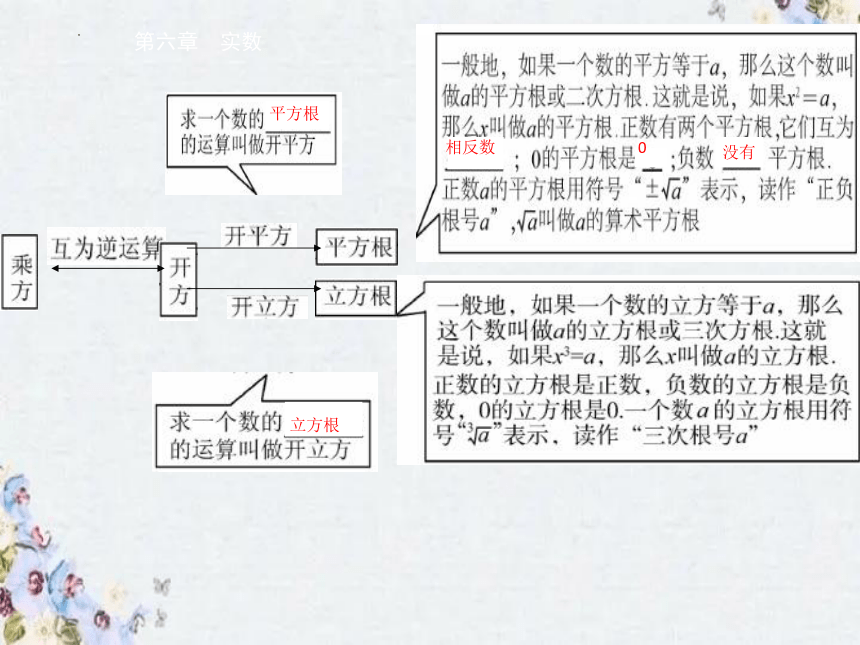
第六章 实数
平方根
相反数
0
没有
立方根
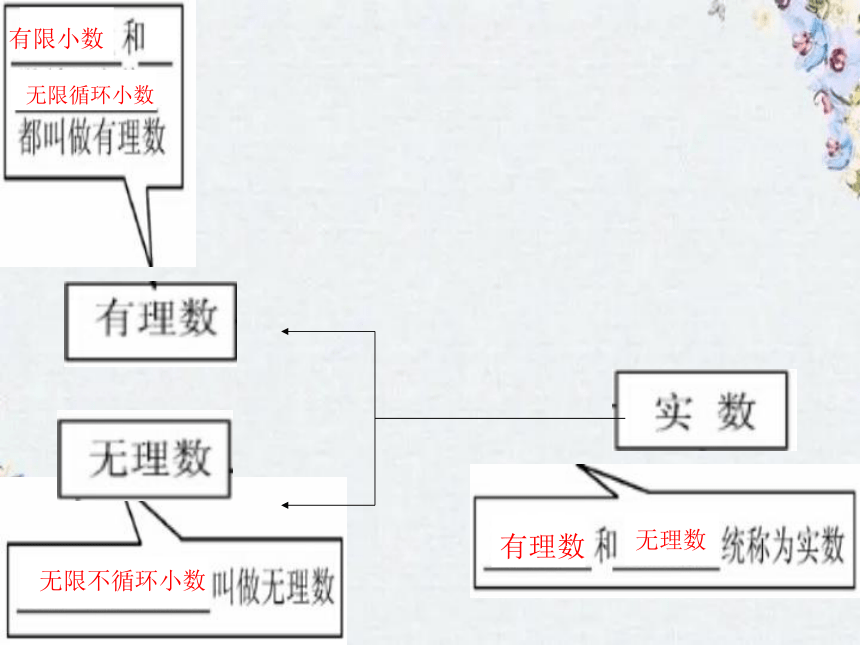
有限小数
无限不循环小数
无限循环小数
有理数
无理数
例1 如果某数的两个平方根分别是2a+3和a-18,那么这个数是( )
A.5 B.-5
C.169 D.±13
C
【针对训练】
1.已知2a-1与a-5是m的平方根,求m的值.
[归纳总结] (1)若a,b互为相反数,则a+b=0,反之亦然;
(2)若a,b互为倒数,则ab=1,反之亦然;
(3)若a,b互为负倒数,则ab=-1,反之亦然;
(4)注意非零实数的绝对值的特点:一个绝对值对应两个互为相反数的数.
第六章 实数
图6-T-1
例3 实数a,b在数轴上对应的点的位置如图6-T-2所示,计算|a-b|的结果为( )
图6-T-2
A.a+b B.a-b
C.b-a D.-a-b
C
【针对训练】
B
第七章 平面直角坐标系
0
0
相等
相等
1、已知点A(-3+a,2a+9)在第二象限的角平分线上,则点a的值是 。
答案:-2
2、点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是 。
3、点P(a-1,a2-9)在x轴负半轴上,则P点坐标是 。
(3 ,-2)
(-4 ,0)
4.点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 。
3个单位
4个单位
(-3 ,-1)
5.直角坐标系中,在y轴上有一点P ,且OP=5,则P的坐标为 。
(0 ,5)或(0 ,-5)
6.已知A(1,4),
B(-4,0),C(2,0). △ABC的面积是____
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
【归纳拓展】一、三象限内点的横、纵坐标同号;二、四象限内点的横、纵坐标异号;平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的距离是它横坐标的绝对值;平行平x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同。
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则点B的坐标是 .
(2,2)或(-2,2)
专题三 求坐标系中的几何图形面积
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个单位
长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A
B
C
A1
B1
C1
A2
B2
C2
A(0,2)
B(4,3)
C(3,0)
5.5
期中复习
人教版 七年级下册
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
(数量关系)
(位置关系)
(数量关系)
平行线的判定与性质的关系图
判定:已知角的关系得平行的关系.证平行,用判定.
性质:已知平行的关系得角的关系.知平行,用性质.
第五章 相交线与平行线
顶点
公
共边
公共边
互为反向延
长线
互补
顶点
顶点
边
相等
不相交
平行
平行
相等
相等
互补
第五章 相交线与平行线
90°
垂足
有且只有
垂线段
垂线段
相等
相等
互补
判断一件事
题设
结论
真命题
假命题
第五章 相交线与平行线
直线
一定
形状
大
小
平行(或在同一条直线上)
且相等
平行(或在同一条直线上)且相等
第六章 实数
平方根
相反数
0
没有
立方根
有限小数
无限不循环小数
无限循环小数
有理数
无理数
例1 如果某数的两个平方根分别是2a+3和a-18,那么这个数是( )
A.5 B.-5
C.169 D.±13
C
【针对训练】
1.已知2a-1与a-5是m的平方根,求m的值.
[归纳总结] (1)若a,b互为相反数,则a+b=0,反之亦然;
(2)若a,b互为倒数,则ab=1,反之亦然;
(3)若a,b互为负倒数,则ab=-1,反之亦然;
(4)注意非零实数的绝对值的特点:一个绝对值对应两个互为相反数的数.
第六章 实数
图6-T-1
例3 实数a,b在数轴上对应的点的位置如图6-T-2所示,计算|a-b|的结果为( )
图6-T-2
A.a+b B.a-b
C.b-a D.-a-b
C
【针对训练】
B
第七章 平面直角坐标系
0
0
相等
相等
1、已知点A(-3+a,2a+9)在第二象限的角平分线上,则点a的值是 。
答案:-2
2、点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是 。
3、点P(a-1,a2-9)在x轴负半轴上,则P点坐标是 。
(3 ,-2)
(-4 ,0)
4.点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 。
3个单位
4个单位
(-3 ,-1)
5.直角坐标系中,在y轴上有一点P ,且OP=5,则P的坐标为 。
(0 ,5)或(0 ,-5)
6.已知A(1,4),
B(-4,0),C(2,0). △ABC的面积是____
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
【归纳拓展】一、三象限内点的横、纵坐标同号;二、四象限内点的横、纵坐标异号;平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的距离是它横坐标的绝对值;平行平x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同。
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则点B的坐标是 .
(2,2)或(-2,2)
专题三 求坐标系中的几何图形面积
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个单位
长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A
B
C
A1
B1
C1
A2
B2
C2
A(0,2)
B(4,3)
C(3,0)
5.5
同课章节目录
