北师大版七年级数学上册 第四章 基本平面图形小结与复习课件(共26张PPT)
文档属性
| 名称 | 北师大版七年级数学上册 第四章 基本平面图形小结与复习课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 920.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第四章 基本平面图形
小结与复习
知识归类
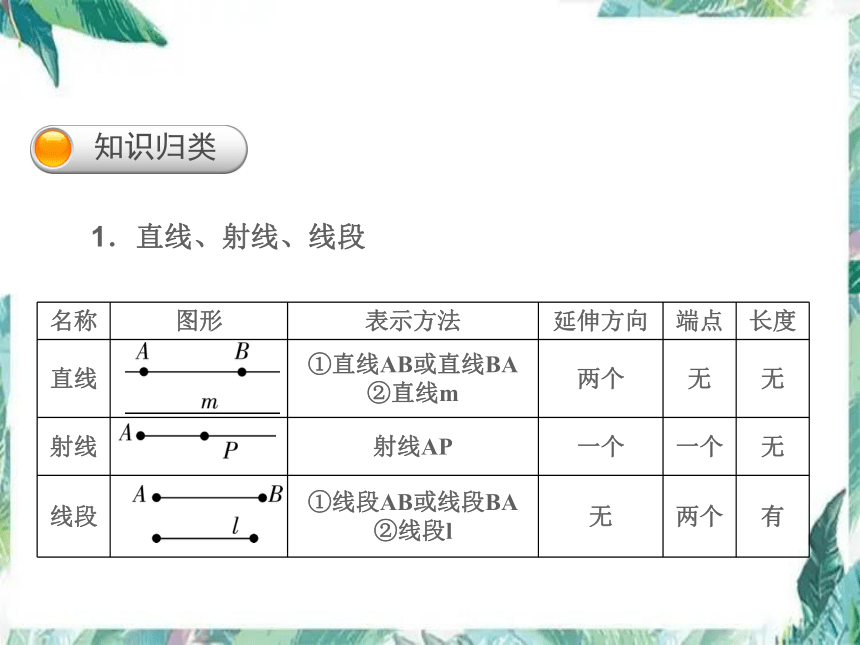
1.直线、射线、线段
名称 图形 表示方法 延伸方向 端点 长度
直线 ①直线AB或直线BA ②直线m 两个 无 无
射线 射线AP 一个 一个 无
线段 ①线段AB或线段BA ②线段l 无 两个 有
2.直线的基本性质
经过两点有且只有____条直线.
3.线段的基本性质
两点之间,____________最短.
4.两点之间的距离
两点之间线段的________,叫做这两点之间的距离.距离是指线段的_______,是一个_______,而不是指线段本身.
5.比较两条线段长短的方法
(1)叠合法:把它们放在同一条_______上比较;
一
线段
长度
长度
数值
直线
第四章 |过关测试
(2)度量法:用刻度尺量出两条线段的长度进行比较.
6.线段的中点
若点M把线段AB分成_______的两条线段AM、BM,则点M叫做线段AB的中点.这时有AM=______=____ ,AB=_______=1/2 ________.
相等
BM
AB
2AM
2BM
第四章 |过关测试
7.角
(1)概念:角由两条具有公共_______的射线组成,两条射线的公共______是这个角的________,这两条射线叫做角的____;从动态观点看,角是一条射线绕_______从起始位置旋转到终止位置所组成的图形.
(2)表示方法:①三个大写英文字母表示,中间的字母表示_______,其他两个字母分别表示两条边上的任意一点;②用一个数字或小写________字母表示;③用一个大写_______字母表示,前提是以这个点为顶点的角只有一个.
端点
端点
顶点
边
端点
顶点
希腊
英文
第四章 |过关测试
(3)单位及换算:把周角平均分成360份,每一份就是1°的角,1°的1/60就是1′,1′的1/60就是1″,即1°= ____,1′=________.
(4)分类:小于平角的角可按大小分成三类:当一个角等于平角的一半时,这个角叫做________;大于0°角小于直角的角叫做________;大于直角而小于平角的角叫做__________.
8.角的平分线
从一个角的_______引出的一条射线,把这个角分成两个_________的角,这条射线叫做这个角的平分线.
60′
60′
直角
锐角
钝角
顶点
相等
考点攻略
考点一 直线、射线、线段
例1 如图4-1,C、D是线段AB上两点,若CB=4 cm,DB=7 cm,且D是AC的中点,则AC的长等于( )
A.3 cm B.6 cm
C.11 cm D.14 cm
[解析] B 先利用线段的和差求出DC的长,再根据线段的中点定义求AC的长.
考点二 角
例2 [2010·呼和浩特] 8点30分时,钟表的时针与分针的夹角为__________°
[答案] 75
[解析] 钟表被分成12格,每格的度数是30°,30°×2.5=75°.
第四章 |过关测试
第四章 |过关测试
考点三 规律探索性问题
例3 [2010·嵊州] 如图4-2,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….则“17”在射线______上;“2007”在射线______上.
[答案] OE OC
第四章 |过关测试
第四章 |过关测试
第四章 |过关测试
试卷讲练
考查 意图 平面图形是七年级数学的重要组成部分,在各类考试中常以填空题、选择题、计算题出现.本卷主要考查了直线、射线、线段、角、角的比较、多边形和圆等,重点考查了线和角. 难易度 易 1,2,3,4,5,6,7,8,9,11,12,13,14,17,18,19,20,23
中 10,15,16,21,22
难 24
第四章 |过关测试
知识 与技能 直线、射线、线段 3,6,7,10,11,12,17,19,20,22
角 1,2,5,18,23
角的比较 4,13,15,16,18,21
多边形和圆的初步认识 8,9,14,24
亮点 第6题方案设计问题,是开发学生智力的好题;21题24题趣味性强,贴近实际,让学生体会数学知识应用的快乐. 第四章 |过关测试
针对第1题训练
1.操场上,小明对小亮说:“你在我的北偏东30°方向上”,那么小亮可以对小明说:“你在我的________方向上”( )
A.南偏西30° B.北偏东30°
C.北偏东60° D.南偏西60°
[答案] A
2.在一次航海中,在一艘货轮的北偏东54°的方向上有一艘渔船,那么货轮在渔船的________方向上.
[答案] 南偏西54°
第四章 |过关测试
针对第10题训练
1.如图4-3所示,A,B,C是一条公路上的三个村庄,A,B间路程为100 km,A,C间路程为40 km,现在A,B之间建一个车站P,设P,C之间的路程为x km.
(1)用含x的代数式表示车站到三个村庄的路程之和;
(2)若路程之和为102 km,则车站应建在何处?
(3)若要使车站到三个村庄的路程总和最小,问车站应建在何处?最小值是多少?
[解析] (1)由图易得AP=AC+PC,BP=100-AP;
(2)让(1)所求得的代数式的值为102,求得x即可;
(3)路程和最小,那么x应最小,此时为0,P与C重合.
解:(1)路程之和为PA+PC+PB=40+x+100-(40+x)+x=(100+x)km;
(2)100+x=102,x=2,车站在C两侧2 km处;
(3)当x=0时,x+100=100,车站建在C处路程和最小,路程和为100 km.
2.(1)如图4-4,A、B、C是三个居住人口数量相同的住宅小区的大门所在位置,且A、B、C三点共线,已知AB=120米,BC=200米,E、F分别是AB、BC的中点,为了方便三个小区的居民出行,公交公司计划在E点或F点设一公交停靠站点,为使从三个小区大门步行到公交停靠点的路程长之和最小,你认为公交车停靠点的位置应设在哪里,为什么?
(2)已知A、B、C三点在一条直线上,如果AB=a,BC=b,且a<b,求线段AB和BC的中点E、F之间的距离.
第四章 |过关测试
[解析] (1)根据图示,先分别计算一下从三个小区大门步行到公交停靠点E、F的路程长之和,然后比较一下大小,路程小的即为所求;
(2)根据题意,画出图示,根据图示找出EF与AB、BC的数量关系.
第四章 |过关测试
解:(1)因为E、F分别是AB、BC的中点,AB=120米,BC=200米,
所以AE=BE=60米,BF=CF=100米;
当公交公司在E点设一公交停靠站点,则从三个小区大门步行到公交停靠点的路程长之和为:
AE+BE+CE=AB+BC+BE=120+200+60=380(米);
当公交公司在F点设一公交停靠站点,则从三个小区大门步行到公交停靠点的路程长之和为:
AF+BF+CF=AB+BF+BC=120+100+200=420(米);
因为380<420,
所以公交车停靠点的位置应该是点E处;
第四章 |过关测试
图4-5
第四章 |过关测试
数学·新课标(BS)
针对第18题训练
计算:
(1)90°-45°32″;
(2)6°32′25″×7.
解:(1)44°28′ (2)45°46′55″
课后练习
见《学练优》本章节“本章热点专练”
第四章 基本平面图形
小结与复习
知识归类
1.直线、射线、线段
名称 图形 表示方法 延伸方向 端点 长度
直线 ①直线AB或直线BA ②直线m 两个 无 无
射线 射线AP 一个 一个 无
线段 ①线段AB或线段BA ②线段l 无 两个 有
2.直线的基本性质
经过两点有且只有____条直线.
3.线段的基本性质
两点之间,____________最短.
4.两点之间的距离
两点之间线段的________,叫做这两点之间的距离.距离是指线段的_______,是一个_______,而不是指线段本身.
5.比较两条线段长短的方法
(1)叠合法:把它们放在同一条_______上比较;
一
线段
长度
长度
数值
直线
第四章 |过关测试
(2)度量法:用刻度尺量出两条线段的长度进行比较.
6.线段的中点
若点M把线段AB分成_______的两条线段AM、BM,则点M叫做线段AB的中点.这时有AM=______=____ ,AB=_______=1/2 ________.
相等
BM
AB
2AM
2BM
第四章 |过关测试
7.角
(1)概念:角由两条具有公共_______的射线组成,两条射线的公共______是这个角的________,这两条射线叫做角的____;从动态观点看,角是一条射线绕_______从起始位置旋转到终止位置所组成的图形.
(2)表示方法:①三个大写英文字母表示,中间的字母表示_______,其他两个字母分别表示两条边上的任意一点;②用一个数字或小写________字母表示;③用一个大写_______字母表示,前提是以这个点为顶点的角只有一个.
端点
端点
顶点
边
端点
顶点
希腊
英文
第四章 |过关测试
(3)单位及换算:把周角平均分成360份,每一份就是1°的角,1°的1/60就是1′,1′的1/60就是1″,即1°= ____,1′=________.
(4)分类:小于平角的角可按大小分成三类:当一个角等于平角的一半时,这个角叫做________;大于0°角小于直角的角叫做________;大于直角而小于平角的角叫做__________.
8.角的平分线
从一个角的_______引出的一条射线,把这个角分成两个_________的角,这条射线叫做这个角的平分线.
60′
60′
直角
锐角
钝角
顶点
相等
考点攻略
考点一 直线、射线、线段
例1 如图4-1,C、D是线段AB上两点,若CB=4 cm,DB=7 cm,且D是AC的中点,则AC的长等于( )
A.3 cm B.6 cm
C.11 cm D.14 cm
[解析] B 先利用线段的和差求出DC的长,再根据线段的中点定义求AC的长.
考点二 角
例2 [2010·呼和浩特] 8点30分时,钟表的时针与分针的夹角为__________°
[答案] 75
[解析] 钟表被分成12格,每格的度数是30°,30°×2.5=75°.
第四章 |过关测试
第四章 |过关测试
考点三 规律探索性问题
例3 [2010·嵊州] 如图4-2,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….则“17”在射线______上;“2007”在射线______上.
[答案] OE OC
第四章 |过关测试
第四章 |过关测试
第四章 |过关测试
试卷讲练
考查 意图 平面图形是七年级数学的重要组成部分,在各类考试中常以填空题、选择题、计算题出现.本卷主要考查了直线、射线、线段、角、角的比较、多边形和圆等,重点考查了线和角. 难易度 易 1,2,3,4,5,6,7,8,9,11,12,13,14,17,18,19,20,23
中 10,15,16,21,22
难 24
第四章 |过关测试
知识 与技能 直线、射线、线段 3,6,7,10,11,12,17,19,20,22
角 1,2,5,18,23
角的比较 4,13,15,16,18,21
多边形和圆的初步认识 8,9,14,24
亮点 第6题方案设计问题,是开发学生智力的好题;21题24题趣味性强,贴近实际,让学生体会数学知识应用的快乐. 第四章 |过关测试
针对第1题训练
1.操场上,小明对小亮说:“你在我的北偏东30°方向上”,那么小亮可以对小明说:“你在我的________方向上”( )
A.南偏西30° B.北偏东30°
C.北偏东60° D.南偏西60°
[答案] A
2.在一次航海中,在一艘货轮的北偏东54°的方向上有一艘渔船,那么货轮在渔船的________方向上.
[答案] 南偏西54°
第四章 |过关测试
针对第10题训练
1.如图4-3所示,A,B,C是一条公路上的三个村庄,A,B间路程为100 km,A,C间路程为40 km,现在A,B之间建一个车站P,设P,C之间的路程为x km.
(1)用含x的代数式表示车站到三个村庄的路程之和;
(2)若路程之和为102 km,则车站应建在何处?
(3)若要使车站到三个村庄的路程总和最小,问车站应建在何处?最小值是多少?
[解析] (1)由图易得AP=AC+PC,BP=100-AP;
(2)让(1)所求得的代数式的值为102,求得x即可;
(3)路程和最小,那么x应最小,此时为0,P与C重合.
解:(1)路程之和为PA+PC+PB=40+x+100-(40+x)+x=(100+x)km;
(2)100+x=102,x=2,车站在C两侧2 km处;
(3)当x=0时,x+100=100,车站建在C处路程和最小,路程和为100 km.
2.(1)如图4-4,A、B、C是三个居住人口数量相同的住宅小区的大门所在位置,且A、B、C三点共线,已知AB=120米,BC=200米,E、F分别是AB、BC的中点,为了方便三个小区的居民出行,公交公司计划在E点或F点设一公交停靠站点,为使从三个小区大门步行到公交停靠点的路程长之和最小,你认为公交车停靠点的位置应设在哪里,为什么?
(2)已知A、B、C三点在一条直线上,如果AB=a,BC=b,且a<b,求线段AB和BC的中点E、F之间的距离.
第四章 |过关测试
[解析] (1)根据图示,先分别计算一下从三个小区大门步行到公交停靠点E、F的路程长之和,然后比较一下大小,路程小的即为所求;
(2)根据题意,画出图示,根据图示找出EF与AB、BC的数量关系.
第四章 |过关测试
解:(1)因为E、F分别是AB、BC的中点,AB=120米,BC=200米,
所以AE=BE=60米,BF=CF=100米;
当公交公司在E点设一公交停靠站点,则从三个小区大门步行到公交停靠点的路程长之和为:
AE+BE+CE=AB+BC+BE=120+200+60=380(米);
当公交公司在F点设一公交停靠站点,则从三个小区大门步行到公交停靠点的路程长之和为:
AF+BF+CF=AB+BF+BC=120+100+200=420(米);
因为380<420,
所以公交车停靠点的位置应该是点E处;
第四章 |过关测试
图4-5
第四章 |过关测试
数学·新课标(BS)
针对第18题训练
计算:
(1)90°-45°32″;
(2)6°32′25″×7.
解:(1)44°28′ (2)45°46′55″
课后练习
见《学练优》本章节“本章热点专练”
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
