北师大版七年级数学上册第五章 一元一次方程 复习课件(共33张PPT)
文档属性
| 名称 | 北师大版七年级数学上册第五章 一元一次方程 复习课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
一元一次方程
复习
一、方程定义:
含有未知数的等式叫做方程。
特征:
(1)含有未知数
(2)等式
判断下列各式哪些是方程,哪些不是?
为什么?
(2)
(4)
(6)
(1)
(3)
(5)
否
是
否
是
是
是
等式的性质是什么?
性质1 等式两边同时加(或减)同一个代数式, 所得结果仍是等式.
性质2 等式两边同时乘同一个数(或除以同一个不为0的数), 所得结果仍是等式.
如果a=b,那么ac=bc;
如果a=b(c≠0的数),那么 =
如果a=b,那么a ± c =b±c
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
练习:判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
使方程左右两边的值相等的未知数的值叫做方程的解.
求方程的解的过程叫解方程。
方程的解
将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项。
关键点:移项一定要变号。
移项
大家判断一下,下列方程的变形是否正确?
为什么?
(1)
(2)
(3)
(4)
(×)
(×)
(×)
(×)
一、一元一次方程定义
(1)只有一个未知数
(2)未知数的次数为1
(3)整式方程
注:三个条件要全部满足
1.判断下列方程是否为一元一次方程?
为什么?
(1)
(5)
(3)
(4)
(2)
(6)
否
是
否
否
否
是
2. 若 是一元一次方程,
则
。
3. 若方程 是一元一次
方程,则 应满足
。
4. 若 是方程
的解,则代数式
。
2
-1
a≠3
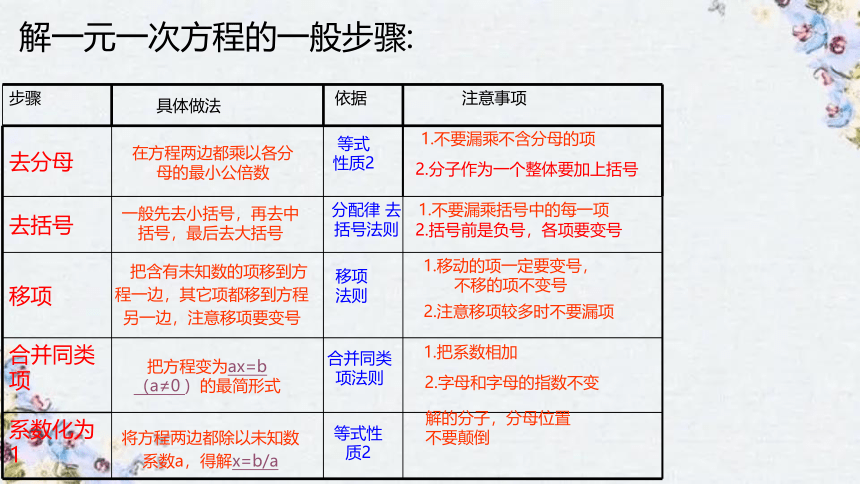
解一元一次方程的一般步骤:
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化为1
在方程两边都乘以各分母的最小公倍数
1.不要漏乘不含分母的项
一般先去小括号,再去中括号,最后去大括号
1.不要漏乘括号中的每一项
把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号
1.移动的项一定要变号,
不移的项不变号
2.注意移项较多时不要漏项
把方程变为ax=b
(a≠0 ) 的最简形式
2.字母和字母的指数不变
将方程两边都除以未知数系数a,得解x=b/a
解的分子,分母位置不要颠倒
1.把系数相加
2.分子作为一个整体要加上括号
2.括号前是负号,各项要变号
移项
法则
合并同类项法则
等式性质2
等式
性质2
分配律 去括号法则
图示解一元一次方程的步骤为
去括号
移 项
合并同类项
系数化为1
去分母
(3)
解下列一元一次方程.
(1)
(2)
(1)
解:
解:
(2)
(3)
解:
例:解下列方程:
解:原方程可化为:
注意:如果分母不是整数的方程可以应用分数的基本性质转化成整数,这样有利于去分母。
去分母, 得5x –(1.5 - x)= 1
去括号,得 5x – 1.5 + x = 1
移项, 得 5x + x = 1 + 1.5
两边同除以6, 得x=
合并同类项得6x=2.5
④
解:
×
6
-
2
×
6
=
6
×
3(3x+1)
-
12=
2(x-1)
3·3x+3×1-12 =
2x
+2×(-1)
9x+3-12=2x-2
9x-2x=-2-3+12
7x=7
X=7÷7
X=1
动手做一做
(5)
解:
(6)
解:
= 3
2.若方程
与方程
的解相同,则a =
。
1.若两个多项式5x+2与-2x+10的值
互为相反数,则(x-2)的值是
-6
2
3.若关于x的方程( m-2)x |m|-1 +3=0是一元一次方程,求这个方程的解.
解:根据题意可知,
∴
即
又∵
∴
∴
当m =-2时,原方程为
解得,
1.审题:弄清题意和题目中的数量关系及相等关系.
2.设元:选择题目中适当的一个未知数用字母表示,并把其它未知量用含字母的代数式表示;
3.列方程:根据相等关系列出方程;
4.解方程:求出未知数的值;
5.检验:检查求得的值是否正确和符合实际情形.
6.写出答案(包括单位名称) .
列一元一次方程解应用题的一般步骤
列方程解应用题常见的类型
1. 和、差、倍、分问题
2. 等积变形问题
3. 调配问题
4. 比例分配问题
5.工程问题
6. 数字问题
8.销售中的利润问题
9.储蓄问题
10.年龄问题
7.行程问题
列方程解应用题时,先弄清题目是属于上面所述的哪种类型的问题,再设出末知数,根据各种类型的数量关系列出方程即可解决问题.
例1 某商店因价格竟争,将某型号彩电按标价的8折出售,此时每台彩电的利润率是5%。此型号彩电的进价为每台4000元,那么彩电的标价是多少?
条件
按标价的8折出售
按8折出售时的利润率是5%
彩电的进价为4000元
——利润率
——进价
问题
彩电的标价是多少?
——标价
——标价的 为售价
___
8
10
彩电售价
–
彩电进价
=
彩电进价
×
彩电的利润率
根据题意找出等量关系:
已知为:5%
彩电标价 ×
___
8
10
已知:4000元
已知:4000元
如果设彩电标价为x元,则根据等量关系可得方程:
×
___
8
10
x
–
4000
=
4000
5%
例1 某商店因价格竟争,将某型号彩电按标价的8折出售,此时每台彩电的利润率是5%。此型号彩电的进价为每台4000元,那么彩电的标价是多少?
解:设此彩电的标价为x元,根据题意,得
×
___
8
10
x
–
4000
=
4000
5%
移项
__
8
10
x
=
4000 × 5% +4000
合并同类项
___
8
10
x
=
4200
系数化为1
x = 5250
答:此彩电的标价为5250元。
例2 学校团委组织65名新团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人搬了4次,共搬了1800块.问这些新团员中有多少名男同学?
8×4
(65-x)
24(65-x)
列表为
32x
x=30
根据题意,列方程得
答: 新团员中有30名男同学
快速解答:小华今年15岁,他爸爸43岁,问:经过几年后小华会是爸爸年龄的1/3 ?
32x+24(65-x)=1800
解:设男同学有x名,女同学有(65-x)名
12. 甲、乙两地相距120千米,一辆汽车和一辆摩托车从两地同时出发相向而行,1.2小时相遇. 相遇后,摩托车继续前进,汽车在相遇处停留10分钟后原速返回,结果在第一次相遇后半小时再次遇到摩托车,问汽车、摩托车每小时各行驶多少千米?
解:设汽车每小时行驶x千米, 摩托车每小时行驶
千米,
根据题意,得 .
解得x=60.
则 -x=40.
答:汽车每小时行驶60千米,摩托车每小时行驶40千米.
13. 一个车间加工轴杆和轴承,每人每天平均可以加工轴杆12根或者轴承16个,1根轴杆与2个轴承为一套,该车间共有90人,应该怎样调配人力,才能使每天生产的轴承和轴杆正好配套?
解:设x个人加工轴杆,(90-x)个人加工轴承,才能使每天生产的轴承和轴杆正好配套,
根据题意,得12x×2=16(90-x).
去括号,得24x=1440-16x.
移项、合并同类项,得40x=1440.
解得x=36. 则90-x=90-36=54.
答:应调配36个人加工轴杆,54个人加工轴承,才能使每天生产的轴承和轴杆正好配套.
14. 春节期间,甲、乙两商场有某品牌服装共450件,由于甲商场销量上升,需从乙商场调运该服装50件,调运后甲商场该服装的数量是乙商场的2倍,求甲、乙两商场原来各自有该品牌服装的数量.
解:设甲商城原来有该品牌服装x件,则乙商城原来有该品牌服装(450-x)件,
根据题意,得x+50=2[(450-x)-50].
解得x=250.
则450-x=450-250=200.
答:甲商城原来有该品牌服装250件,乙商城原来有该品牌服装200件.
谢 谢
一元一次方程
复习
一、方程定义:
含有未知数的等式叫做方程。
特征:
(1)含有未知数
(2)等式
判断下列各式哪些是方程,哪些不是?
为什么?
(2)
(4)
(6)
(1)
(3)
(5)
否
是
否
是
是
是
等式的性质是什么?
性质1 等式两边同时加(或减)同一个代数式, 所得结果仍是等式.
性质2 等式两边同时乘同一个数(或除以同一个不为0的数), 所得结果仍是等式.
如果a=b,那么ac=bc;
如果a=b(c≠0的数),那么 =
如果a=b,那么a ± c =b±c
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
练习:判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
使方程左右两边的值相等的未知数的值叫做方程的解.
求方程的解的过程叫解方程。
方程的解
将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项。
关键点:移项一定要变号。
移项
大家判断一下,下列方程的变形是否正确?
为什么?
(1)
(2)
(3)
(4)
(×)
(×)
(×)
(×)
一、一元一次方程定义
(1)只有一个未知数
(2)未知数的次数为1
(3)整式方程
注:三个条件要全部满足
1.判断下列方程是否为一元一次方程?
为什么?
(1)
(5)
(3)
(4)
(2)
(6)
否
是
否
否
否
是
2. 若 是一元一次方程,
则
。
3. 若方程 是一元一次
方程,则 应满足
。
4. 若 是方程
的解,则代数式
。
2
-1
a≠3
解一元一次方程的一般步骤:
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化为1
在方程两边都乘以各分母的最小公倍数
1.不要漏乘不含分母的项
一般先去小括号,再去中括号,最后去大括号
1.不要漏乘括号中的每一项
把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号
1.移动的项一定要变号,
不移的项不变号
2.注意移项较多时不要漏项
把方程变为ax=b
(a≠0 ) 的最简形式
2.字母和字母的指数不变
将方程两边都除以未知数系数a,得解x=b/a
解的分子,分母位置不要颠倒
1.把系数相加
2.分子作为一个整体要加上括号
2.括号前是负号,各项要变号
移项
法则
合并同类项法则
等式性质2
等式
性质2
分配律 去括号法则
图示解一元一次方程的步骤为
去括号
移 项
合并同类项
系数化为1
去分母
(3)
解下列一元一次方程.
(1)
(2)
(1)
解:
解:
(2)
(3)
解:
例:解下列方程:
解:原方程可化为:
注意:如果分母不是整数的方程可以应用分数的基本性质转化成整数,这样有利于去分母。
去分母, 得5x –(1.5 - x)= 1
去括号,得 5x – 1.5 + x = 1
移项, 得 5x + x = 1 + 1.5
两边同除以6, 得x=
合并同类项得6x=2.5
④
解:
×
6
-
2
×
6
=
6
×
3(3x+1)
-
12=
2(x-1)
3·3x+3×1-12 =
2x
+2×(-1)
9x+3-12=2x-2
9x-2x=-2-3+12
7x=7
X=7÷7
X=1
动手做一做
(5)
解:
(6)
解:
= 3
2.若方程
与方程
的解相同,则a =
。
1.若两个多项式5x+2与-2x+10的值
互为相反数,则(x-2)的值是
-6
2
3.若关于x的方程( m-2)x |m|-1 +3=0是一元一次方程,求这个方程的解.
解:根据题意可知,
∴
即
又∵
∴
∴
当m =-2时,原方程为
解得,
1.审题:弄清题意和题目中的数量关系及相等关系.
2.设元:选择题目中适当的一个未知数用字母表示,并把其它未知量用含字母的代数式表示;
3.列方程:根据相等关系列出方程;
4.解方程:求出未知数的值;
5.检验:检查求得的值是否正确和符合实际情形.
6.写出答案(包括单位名称) .
列一元一次方程解应用题的一般步骤
列方程解应用题常见的类型
1. 和、差、倍、分问题
2. 等积变形问题
3. 调配问题
4. 比例分配问题
5.工程问题
6. 数字问题
8.销售中的利润问题
9.储蓄问题
10.年龄问题
7.行程问题
列方程解应用题时,先弄清题目是属于上面所述的哪种类型的问题,再设出末知数,根据各种类型的数量关系列出方程即可解决问题.
例1 某商店因价格竟争,将某型号彩电按标价的8折出售,此时每台彩电的利润率是5%。此型号彩电的进价为每台4000元,那么彩电的标价是多少?
条件
按标价的8折出售
按8折出售时的利润率是5%
彩电的进价为4000元
——利润率
——进价
问题
彩电的标价是多少?
——标价
——标价的 为售价
___
8
10
彩电售价
–
彩电进价
=
彩电进价
×
彩电的利润率
根据题意找出等量关系:
已知为:5%
彩电标价 ×
___
8
10
已知:4000元
已知:4000元
如果设彩电标价为x元,则根据等量关系可得方程:
×
___
8
10
x
–
4000
=
4000
5%
例1 某商店因价格竟争,将某型号彩电按标价的8折出售,此时每台彩电的利润率是5%。此型号彩电的进价为每台4000元,那么彩电的标价是多少?
解:设此彩电的标价为x元,根据题意,得
×
___
8
10
x
–
4000
=
4000
5%
移项
__
8
10
x
=
4000 × 5% +4000
合并同类项
___
8
10
x
=
4200
系数化为1
x = 5250
答:此彩电的标价为5250元。
例2 学校团委组织65名新团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人搬了4次,共搬了1800块.问这些新团员中有多少名男同学?
8×4
(65-x)
24(65-x)
列表为
32x
x=30
根据题意,列方程得
答: 新团员中有30名男同学
快速解答:小华今年15岁,他爸爸43岁,问:经过几年后小华会是爸爸年龄的1/3 ?
32x+24(65-x)=1800
解:设男同学有x名,女同学有(65-x)名
12. 甲、乙两地相距120千米,一辆汽车和一辆摩托车从两地同时出发相向而行,1.2小时相遇. 相遇后,摩托车继续前进,汽车在相遇处停留10分钟后原速返回,结果在第一次相遇后半小时再次遇到摩托车,问汽车、摩托车每小时各行驶多少千米?
解:设汽车每小时行驶x千米, 摩托车每小时行驶
千米,
根据题意,得 .
解得x=60.
则 -x=40.
答:汽车每小时行驶60千米,摩托车每小时行驶40千米.
13. 一个车间加工轴杆和轴承,每人每天平均可以加工轴杆12根或者轴承16个,1根轴杆与2个轴承为一套,该车间共有90人,应该怎样调配人力,才能使每天生产的轴承和轴杆正好配套?
解:设x个人加工轴杆,(90-x)个人加工轴承,才能使每天生产的轴承和轴杆正好配套,
根据题意,得12x×2=16(90-x).
去括号,得24x=1440-16x.
移项、合并同类项,得40x=1440.
解得x=36. 则90-x=90-36=54.
答:应调配36个人加工轴杆,54个人加工轴承,才能使每天生产的轴承和轴杆正好配套.
14. 春节期间,甲、乙两商场有某品牌服装共450件,由于甲商场销量上升,需从乙商场调运该服装50件,调运后甲商场该服装的数量是乙商场的2倍,求甲、乙两商场原来各自有该品牌服装的数量.
解:设甲商城原来有该品牌服装x件,则乙商城原来有该品牌服装(450-x)件,
根据题意,得x+50=2[(450-x)-50].
解得x=250.
则450-x=450-250=200.
答:甲商城原来有该品牌服装250件,乙商城原来有该品牌服装200件.
谢 谢
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
