北师大版九年级上册数学 4.4.4黄金分割 课件(共31张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 4.4.4黄金分割 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 15:07:23 | ||
图片预览





文档简介
(共31张PPT)
——以数学的视角感受美
学习目标
1、理解黄金分割的定义;会判断线段上的某一点是否是黄金分割点;
2、会找一条线段的黄金分割点。
3.在实际操作过程中增强实践意识和自信心。
4.通过建筑,摄影,绘画等的实例了解黄金分割,体会其中的文化价值。
重点:黄金分割的概念,能做出一条线段的黄金分割点
难点:用黄金分割解决实际问题。
发现美
探索美
创造美
应用美
延伸美
留住美
一 发现美
摄影作品之美
你觉得哪张照片的构图最合理?更能体现小松鼠若有所思的在凝视前方?
芭蕾舞演员做相同的动作,踮脚尖和不踮脚尖,哪个更美?
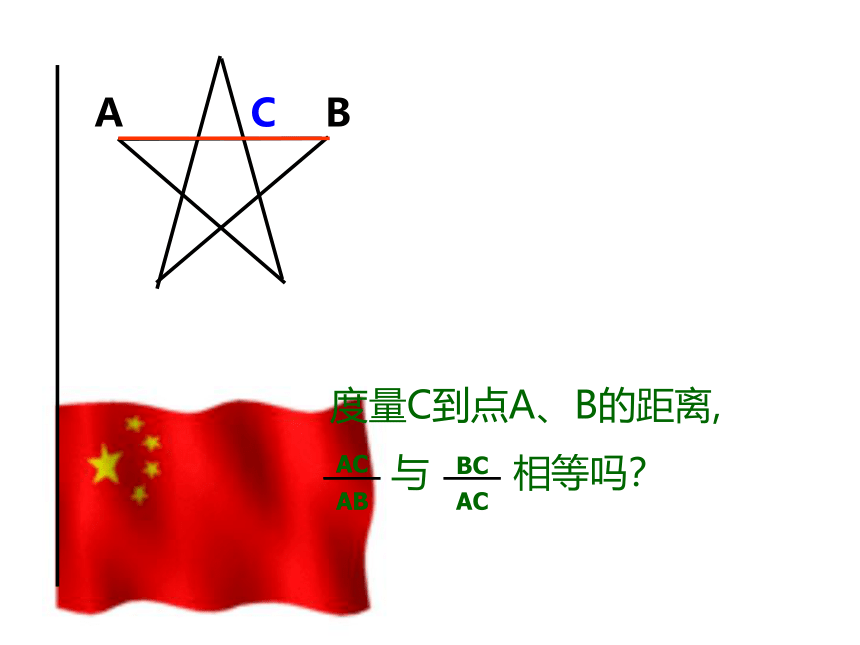
二.探索美
度量C到点A、B的距离,
AC
AB
AC
BC
与 相等吗?
A
C
B
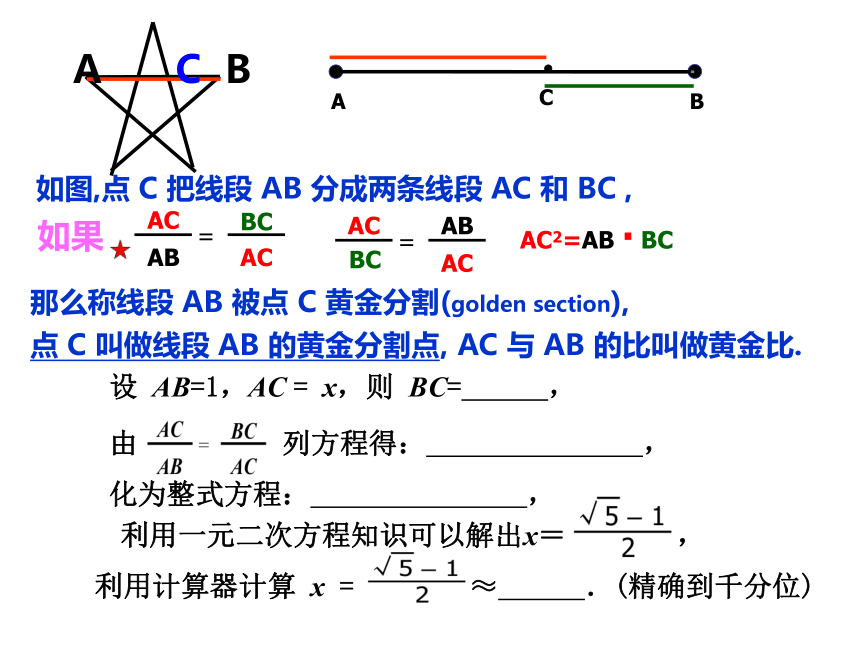
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割(golden section),
点 C 叫做线段 AB 的黄金分割点,
AC 与 AB 的比叫做黄金比.
C
A
B
A
C
B
AC
AB
AC
BC
=
AC2=AB BC
设 AB=1,AC = x,则 BC= ,
由 列方程得: ,
化为整式方程: ,
利用一元二次方程知识可以解出x= ,
利用计算器计算 x = ≈ .(精确到千分位)
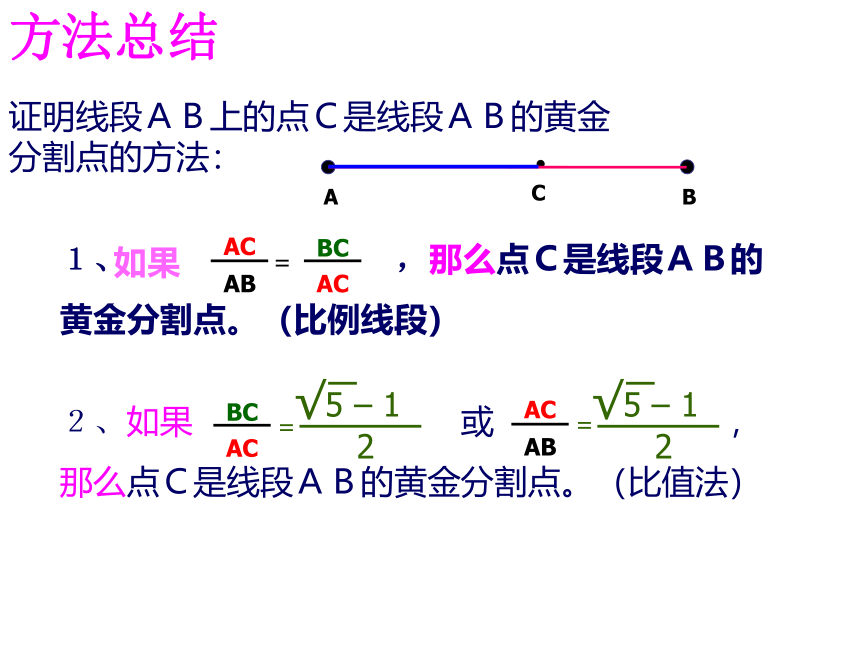
方法总结
证明线段AB上的点C是线段AB的黄金分割点的方法:
C
A
B
如果
AC
AB
AC
BC
=
1、 ,那么点C是线段AB的
黄金分割点。(比例线段)
√5 – 1
2
AC
BC
=
=
AC
AB
√5 – 1
2
2、如果 或 ,
那么点C是线段AB的黄金分割点。(比值法)
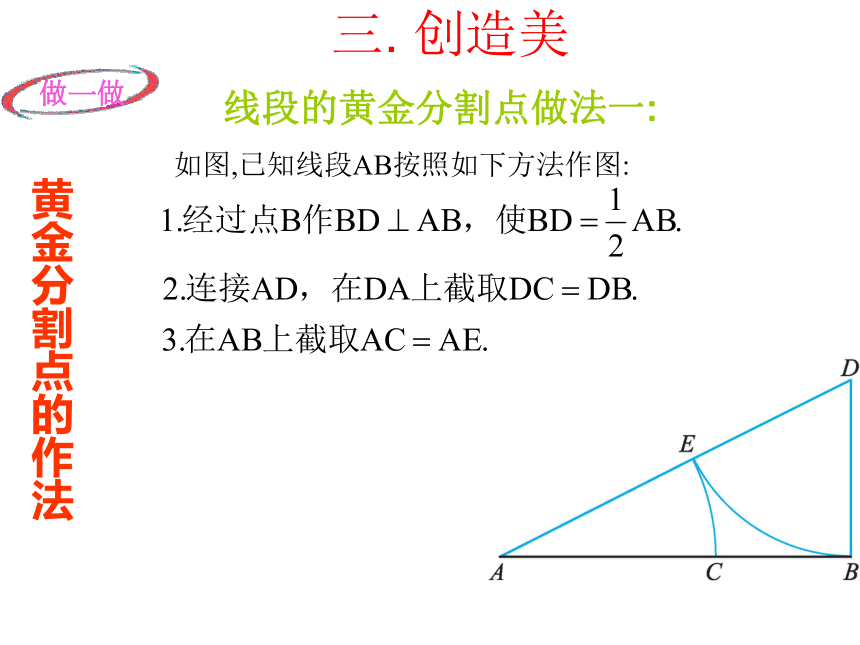
如图,已知线段AB按照如下方法作图:
做一做
黄金分割点的作法
线段的黄金分割点做法一:
三. 创造美
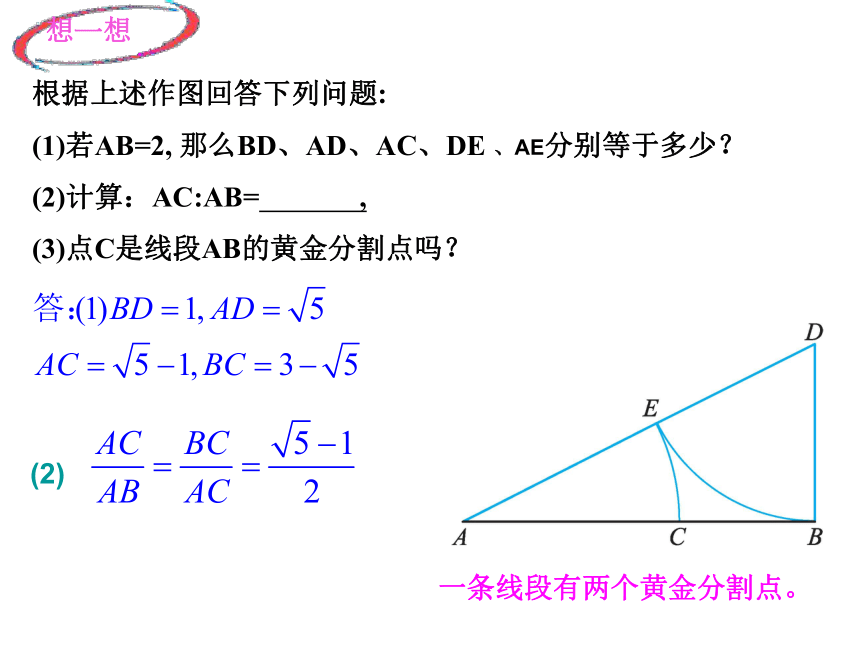
根据上述作图回答下列问题:
(1)若AB=2, 那么BD、AD、AC、DE 、AE分别等于多少?
(2)计算:AC:AB= ,
(3)点C是线段AB的黄金分割点吗?
想一想
一条线段有两个黄金分割点。
(2)
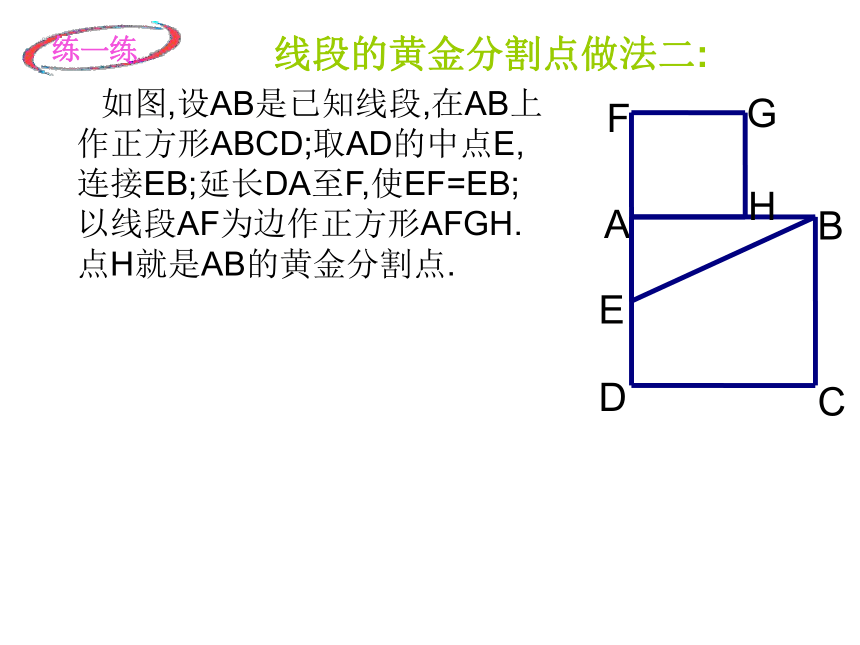
线段的黄金分割点做法二:
如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.
A
G
H
F
E
C
D
B
练一练
A
G
H
F
E
C
D
B
练一练
如果设AB=2,试说明点H是线段AB的
黄金分割点 。
2
1
议一议
你能否利用线段上作出的两个黄金分割点作出五角星?
C
A
B
D
1、作线段AB,并作AB的两个黄金分割点C、D;
2、分别以点D、点C为圆心,以AD长为半径画弧,两弧交于点E,连接DE、CE得等腰三角形DEC;
3、分别延长ED、EC到点F和点G,使EF=EG=AB;
4、连接AG、BF。
C
D
B
A
E
G
F
如果用图中的虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,
那么我们可以惊奇的发现, 。点E是AB的
黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
BC
BE
BC
AB
=
D
F
C
A
E
B
四 应用美
巴台农神庙
想一想
F
D
C
A
E
B
BC
BE
BC
AB
=
1.点E是AB的黄金分割点吗?
2.矩形ABCD的宽与长的比是
黄金比吗?
BC
AB
BC
BE
=
AE
AB
AE
BE
=
点E是AB的黄金分割点
AE
AB
(即 )是黄金比
BC
AB
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形
比例的性质
BC=AE
黄金矩形的“迷人面容”----蒙娜丽莎的微笑。
这幅《蒙娜丽莎的微笑》给了数以亿万计的人们美的艺术享受,备受推崇。意大利画家达芬奇在创作中大量运用了黄金矩形来构图。整个画面使人觉得和谐自然,优雅安宁。
世界艺术珍品——维纳斯女神
,她是西元前一
百多年希腊雕塑鼎盛时
期的代表作,
她的上半
身和下半身的比值接近
0.618.
古埃及胡夫金字塔
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边长与高这比都接近于0.618.
巴黎圣母院
东方明珠塔,塔高462.85米。设计师将在295米处设计了一个上球体,使平直单调的塔身变得丰富多彩,非常协调、美观。
黄金建筑设计
京剧演员经常选择舞台宽度的一个黄金分割点作为出场亮相的位置.
A
C
B
A
C
B
A
C
B
在礼品包装中,也经常用到黄金分割.
1.据有关测定,当气温处于人体正常体温的黄金比值时,人体感到最舒适。因此夏天使用空调时室内温度调到什么温度最适合。
2.在人体下半身与身高的比例上,越接近0.618,越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
五 延伸美
课堂小 结 :
1.黄金分割的概念;
2.黄金分割点的判断;
3.通过作图找到一条线段的黄金分割点,并利用已学知识给予了说明。
六 留住美
2.分组搜集黄金分割资料,制作剪贴报.其中包含一幅利用黄金分割的构图方法摄制的摄影作品.
C
A
B
1、作一个黄金矩形。
同学们,学完本节课你有什么样的感想呢?
你认为数学就是一种美的科学吗?是的,我们的
数学本来就是美的,美就在我们身边。中学时期
是人生的黄金时期,只要我们善于探索,勇于创新,
就一定能创造美好的未来。
课后寄语
——以数学的视角感受美
学习目标
1、理解黄金分割的定义;会判断线段上的某一点是否是黄金分割点;
2、会找一条线段的黄金分割点。
3.在实际操作过程中增强实践意识和自信心。
4.通过建筑,摄影,绘画等的实例了解黄金分割,体会其中的文化价值。
重点:黄金分割的概念,能做出一条线段的黄金分割点
难点:用黄金分割解决实际问题。
发现美
探索美
创造美
应用美
延伸美
留住美
一 发现美
摄影作品之美
你觉得哪张照片的构图最合理?更能体现小松鼠若有所思的在凝视前方?
芭蕾舞演员做相同的动作,踮脚尖和不踮脚尖,哪个更美?
二.探索美
度量C到点A、B的距离,
AC
AB
AC
BC
与 相等吗?
A
C
B
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割(golden section),
点 C 叫做线段 AB 的黄金分割点,
AC 与 AB 的比叫做黄金比.
C
A
B
A
C
B
AC
AB
AC
BC
=
AC2=AB BC
设 AB=1,AC = x,则 BC= ,
由 列方程得: ,
化为整式方程: ,
利用一元二次方程知识可以解出x= ,
利用计算器计算 x = ≈ .(精确到千分位)
方法总结
证明线段AB上的点C是线段AB的黄金分割点的方法:
C
A
B
如果
AC
AB
AC
BC
=
1、 ,那么点C是线段AB的
黄金分割点。(比例线段)
√5 – 1
2
AC
BC
=
=
AC
AB
√5 – 1
2
2、如果 或 ,
那么点C是线段AB的黄金分割点。(比值法)
如图,已知线段AB按照如下方法作图:
做一做
黄金分割点的作法
线段的黄金分割点做法一:
三. 创造美
根据上述作图回答下列问题:
(1)若AB=2, 那么BD、AD、AC、DE 、AE分别等于多少?
(2)计算:AC:AB= ,
(3)点C是线段AB的黄金分割点吗?
想一想
一条线段有两个黄金分割点。
(2)
线段的黄金分割点做法二:
如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.
A
G
H
F
E
C
D
B
练一练
A
G
H
F
E
C
D
B
练一练
如果设AB=2,试说明点H是线段AB的
黄金分割点 。
2
1
议一议
你能否利用线段上作出的两个黄金分割点作出五角星?
C
A
B
D
1、作线段AB,并作AB的两个黄金分割点C、D;
2、分别以点D、点C为圆心,以AD长为半径画弧,两弧交于点E,连接DE、CE得等腰三角形DEC;
3、分别延长ED、EC到点F和点G,使EF=EG=AB;
4、连接AG、BF。
C
D
B
A
E
G
F
如果用图中的虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,
那么我们可以惊奇的发现, 。点E是AB的
黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
BC
BE
BC
AB
=
D
F
C
A
E
B
四 应用美
巴台农神庙
想一想
F
D
C
A
E
B
BC
BE
BC
AB
=
1.点E是AB的黄金分割点吗?
2.矩形ABCD的宽与长的比是
黄金比吗?
BC
AB
BC
BE
=
AE
AB
AE
BE
=
点E是AB的黄金分割点
AE
AB
(即 )是黄金比
BC
AB
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形
比例的性质
BC=AE
黄金矩形的“迷人面容”----蒙娜丽莎的微笑。
这幅《蒙娜丽莎的微笑》给了数以亿万计的人们美的艺术享受,备受推崇。意大利画家达芬奇在创作中大量运用了黄金矩形来构图。整个画面使人觉得和谐自然,优雅安宁。
世界艺术珍品——维纳斯女神
,她是西元前一
百多年希腊雕塑鼎盛时
期的代表作,
她的上半
身和下半身的比值接近
0.618.
古埃及胡夫金字塔
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边长与高这比都接近于0.618.
巴黎圣母院
东方明珠塔,塔高462.85米。设计师将在295米处设计了一个上球体,使平直单调的塔身变得丰富多彩,非常协调、美观。
黄金建筑设计
京剧演员经常选择舞台宽度的一个黄金分割点作为出场亮相的位置.
A
C
B
A
C
B
A
C
B
在礼品包装中,也经常用到黄金分割.
1.据有关测定,当气温处于人体正常体温的黄金比值时,人体感到最舒适。因此夏天使用空调时室内温度调到什么温度最适合。
2.在人体下半身与身高的比例上,越接近0.618,越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
五 延伸美
课堂小 结 :
1.黄金分割的概念;
2.黄金分割点的判断;
3.通过作图找到一条线段的黄金分割点,并利用已学知识给予了说明。
六 留住美
2.分组搜集黄金分割资料,制作剪贴报.其中包含一幅利用黄金分割的构图方法摄制的摄影作品.
C
A
B
1、作一个黄金矩形。
同学们,学完本节课你有什么样的感想呢?
你认为数学就是一种美的科学吗?是的,我们的
数学本来就是美的,美就在我们身边。中学时期
是人生的黄金时期,只要我们善于探索,勇于创新,
就一定能创造美好的未来。
课后寄语
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
