高中物理人教版(2019)选择性必修第一册2.5实验:用单摆测量重力加速度学案(含答案)
文档属性
| 名称 | 高中物理人教版(2019)选择性必修第一册2.5实验:用单摆测量重力加速度学案(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 260.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-10-26 15:50:46 | ||
图片预览


文档简介
2.5 实验:用单摆测量重力加速度
学习目标
1、理解用单摆测重力加速度的思路与科学探究方法。
2、学会用公式法或图像法处理实验数据。
重点难点
1、理解利用单摆测量重力加速度。(重点)
2、掌握用图像处理实验数据的方法。(重点)
3、测量摆长的准确性,计时的准确性,计数的准确性。(难点)
4、实验数据的处理方法。(难点)
自主探究
一、实验目的:学会用单摆测定当地重力加速度,正确熟练使用秒表。
二、实验器材:小金属球、细尼龙线、铁夹、铁架台、游标卡尺、米尺、秒表。
三、实验原理:
根据单摆周期公式,得: 。据此,只要测得摆长l和周期T,即可算出当地的重力加速度g。
四、实验步骤
1、做单摆:在细线的一端打一比小球上的孔径稍大些的结,将细线穿过球上的小孔,然后把线的上端用铁夹固定于铁架台上,在平衡位置处作上标记。
2、测摆长:用毫米刻度尺测出摆线长度,用游标卡尺测出摆球的直径d,则单摆的摆长。也可用刻度尺直接测量悬点到球心的距离。
3、测周期:将单摆从平衡位置拉开一个小于5度的角,然后释放摆球,当单摆振动稳定后,经过平衡位置时开始用秒表计时,测量N次(一般取次)全振动的时间t,则周期。
4、变摆长:将单摆的摆长变短(或变长),重复实验三次,测出相应的摆长l和周期T。
五、数据分析
1、平均值法:每改变一次摆长,将相应的l和T代入公式中求出g值,最后求出g的平均值。
设计如下所示实验表格
实验次数 摆长l/m 周期T/s 重力加速度g/() 重力加速度g的平均值/()
1
2
3
2、图像法:由得,作出图像,即以为纵轴,以l为横轴。其斜率,由图像的斜率即可求出重力加速度g。
六、误差分析
1、系统误差:主要来源于单摆模型本身是否符合要求。即:悬点是否固定,摆球是否可看作质点,球、线是否符合要求,摆动是否在同一竖直平面内以及摆长的测量是否精确等。
2、偶然误差:主要源于周期的测量误差,应取多个全振动的总时间t,求平均值作为周期的测量值。
七、注意事项
1、选择材料时应选择较细又不易伸长的线,长度一般在1m左右,小球应选用密度较大的金属球,直径应较小,最好不超过2 cm。
2、单摆悬线的上端不可随意卷在铁夹的杆上,应用铁夹夹紧,以免摆动时发生摆线下滑、摆长改变的现象。
3、注意摆动时控制摆线偏离竖直方向不超过5°。
4、摆球振动时,要使之保持在同一个竖直平面内,不要形成圆锥摆。
经典例题
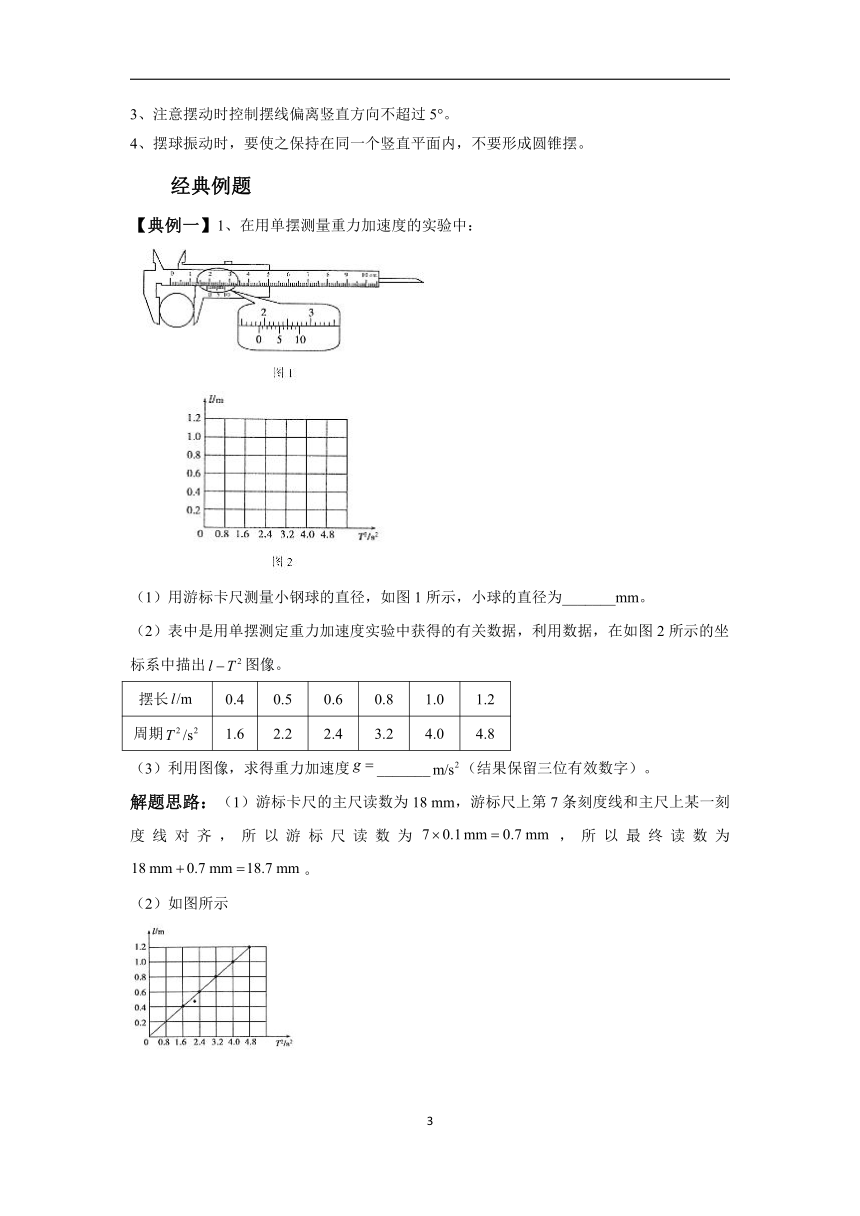
【典例一】1、在用单摆测量重力加速度的实验中:
(1)用游标卡尺测量小钢球的直径,如图1所示,小球的直径为_______mm。
(2)表中是用单摆测定重力加速度实验中获得的有关数据,利用数据,在如图2所示的坐标系中描出图像。
摆长 0.4 0.5 0.6 0.8 1.0 1.2
周期 1.6 2.2 2.4 3.2 4.0 4.8
(3)利用图像,求得重力加速度_______(结果保留三位有效数字)。
解题思路:(1)游标卡尺的主尺读数为18 mm,游标尺上第7条刻度线和主尺上某一刻度线对齐,所以游标尺读数为,所以最终读数为。
(2)如图所示
(3)根据单摆的周期公式得,则图线的斜率为,得。
答案:(1)18.7
(2)见解析
(3)9.86(9.85~9.87)
【典例二】2、在“用单摆测定重力加速度”的实验中:
(1)为了减小测量周期的误差,计时开始时,摆球应是经过最_____(填“高”或“低”)点的位置,且用秒表测量单摆完成多次全振动所用的时间,求出周期。图甲中秒表示数为一单摆全振动50次所经过的时间,则单摆振动周期为______s。
(2)若测得的g值偏大。可能的原因是( )
A.摆球质量过大
B.单摆振动时振幅较小
C.测量摆长时。只考虑了线长.忽略了小球的半径
D.测量周期时。把n个全振动误认为()个全振动.使周期偏小
解题思路:(1)小球的偏角α在很小()时,小球的振动才近似看成简谐运动。在摆球经过最低点时开始计时,产生的时间误差较小。
由秒表读出时间:;
周期;
(2)根据单摆的周期公式则有:
A.单摆的振动与摆的质量无关,故A错误;
B.摆的振动周期与振幅无关,故B错误。
C.测量摆长时。只考虑了线长。忽略了小球的半径,则使摆长测量值偏小,根据公式可知,测得出的重力加速度偏小,故C错误;
D.实验中n个全振动误认为(n+1)个全振动,测得周期偏小,则测得的重力加速度偏大。故D正确。
故选:D
答案:(1)低;99.8
(2)D
随堂训练
1、在“用单摆测定重力加速度”的实验中,
(1)测摆长时,若正确测出悬线长和摆球直径,则摆长为 ;
(2)测周期时,当摆球经过 位置(填平衡位置或最高点)时开始计时并计数次,测出经过该位置N次(约次)的时间为t,则周期为 。
答案:(1) (2) 平衡 ;
2、某同学在做“利用单摆测重力加速度”的实验时,先测得摆线长,摆球直径,然后用秒表记录了单摆全振动50次所用的时间,则
(1)他测得的重力加速度___________.(,结果保留三位有效数字)
(2)他测得的g值偏小,可能的原因是( )
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点上,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将49次全振动记为50次
(3)为了提高实验精度,在实验中可改变几次摆线长并测出相应的周期T,从而得到几组与T的数据,再以为横坐标,为纵坐标,将所得数据描点连成直线,并求得该直线的斜率为k,则重力加速度_____________(用k表示).
答案:(1)9.77 (2)B (3)
3、利用单摆测当地重力加速度的实验中
①利用游标卡尺测得金属小球直径如图丁所示,小球直径______;
②甲乙两个学习小组分别利用单摆测量重力加速度。甲组同学采用图甲所示的实验装置;
A.为比较准确地测量出当地重力加速度的数值,除秒表外,在下列器材中,还应该选用______;(用器材前的字母表示)
a.长度接近的细绳
b.长度为左右的细绳
c.直径为的塑料球
d.直径为的铁球
e.最小刻度为的米尺
f.最小刻度为的米尺
B.该组同学先测出悬点到小球球心的距离,然后用秒表测出单摆完成次全振动所用的时间t。请写出重力加速度的表达式______。(用所测物理量表示)
C.在测量摆长后,测量周期时,摆球振动过程中悬点处摆线的固定出现松动,摆长略微变长,这将会导致所测重力加速度的数值______。(选填“偏大”、“偏小”或“不变”)
③乙组同学在图甲所示装置的基础上再增加一个速度传感器,如图乙所示。将摆球拉开一小角度使其做简谐运动,速度传感器记录了摆球振动过程中速度随时间变化的关系,如图丙所示的图线。
A.由图丙可知,该单摆的周期______;
B.更换摆线长度后,多次测量,根据实验数据,利用计算机作出(周期平方-摆长)图线,并根据图线拟合得到方程。由此可以得出当地的重力加速度______,(取,结果保留3位有效数字)
④某同学在实验过程中,摆长没有加小球的半径,其它操作无误,那么他得到的实验图象可能是下列图象中的______。
答案:①22.6
②adf;;偏小
③2.0;9.76
④B
2
学习目标
1、理解用单摆测重力加速度的思路与科学探究方法。
2、学会用公式法或图像法处理实验数据。
重点难点
1、理解利用单摆测量重力加速度。(重点)
2、掌握用图像处理实验数据的方法。(重点)
3、测量摆长的准确性,计时的准确性,计数的准确性。(难点)
4、实验数据的处理方法。(难点)
自主探究
一、实验目的:学会用单摆测定当地重力加速度,正确熟练使用秒表。
二、实验器材:小金属球、细尼龙线、铁夹、铁架台、游标卡尺、米尺、秒表。
三、实验原理:
根据单摆周期公式,得: 。据此,只要测得摆长l和周期T,即可算出当地的重力加速度g。
四、实验步骤
1、做单摆:在细线的一端打一比小球上的孔径稍大些的结,将细线穿过球上的小孔,然后把线的上端用铁夹固定于铁架台上,在平衡位置处作上标记。
2、测摆长:用毫米刻度尺测出摆线长度,用游标卡尺测出摆球的直径d,则单摆的摆长。也可用刻度尺直接测量悬点到球心的距离。
3、测周期:将单摆从平衡位置拉开一个小于5度的角,然后释放摆球,当单摆振动稳定后,经过平衡位置时开始用秒表计时,测量N次(一般取次)全振动的时间t,则周期。
4、变摆长:将单摆的摆长变短(或变长),重复实验三次,测出相应的摆长l和周期T。
五、数据分析
1、平均值法:每改变一次摆长,将相应的l和T代入公式中求出g值,最后求出g的平均值。
设计如下所示实验表格
实验次数 摆长l/m 周期T/s 重力加速度g/() 重力加速度g的平均值/()
1
2
3
2、图像法:由得,作出图像,即以为纵轴,以l为横轴。其斜率,由图像的斜率即可求出重力加速度g。
六、误差分析
1、系统误差:主要来源于单摆模型本身是否符合要求。即:悬点是否固定,摆球是否可看作质点,球、线是否符合要求,摆动是否在同一竖直平面内以及摆长的测量是否精确等。
2、偶然误差:主要源于周期的测量误差,应取多个全振动的总时间t,求平均值作为周期的测量值。
七、注意事项
1、选择材料时应选择较细又不易伸长的线,长度一般在1m左右,小球应选用密度较大的金属球,直径应较小,最好不超过2 cm。
2、单摆悬线的上端不可随意卷在铁夹的杆上,应用铁夹夹紧,以免摆动时发生摆线下滑、摆长改变的现象。
3、注意摆动时控制摆线偏离竖直方向不超过5°。
4、摆球振动时,要使之保持在同一个竖直平面内,不要形成圆锥摆。
经典例题
【典例一】1、在用单摆测量重力加速度的实验中:
(1)用游标卡尺测量小钢球的直径,如图1所示,小球的直径为_______mm。
(2)表中是用单摆测定重力加速度实验中获得的有关数据,利用数据,在如图2所示的坐标系中描出图像。
摆长 0.4 0.5 0.6 0.8 1.0 1.2
周期 1.6 2.2 2.4 3.2 4.0 4.8
(3)利用图像,求得重力加速度_______(结果保留三位有效数字)。
解题思路:(1)游标卡尺的主尺读数为18 mm,游标尺上第7条刻度线和主尺上某一刻度线对齐,所以游标尺读数为,所以最终读数为。
(2)如图所示
(3)根据单摆的周期公式得,则图线的斜率为,得。
答案:(1)18.7
(2)见解析
(3)9.86(9.85~9.87)
【典例二】2、在“用单摆测定重力加速度”的实验中:
(1)为了减小测量周期的误差,计时开始时,摆球应是经过最_____(填“高”或“低”)点的位置,且用秒表测量单摆完成多次全振动所用的时间,求出周期。图甲中秒表示数为一单摆全振动50次所经过的时间,则单摆振动周期为______s。
(2)若测得的g值偏大。可能的原因是( )
A.摆球质量过大
B.单摆振动时振幅较小
C.测量摆长时。只考虑了线长.忽略了小球的半径
D.测量周期时。把n个全振动误认为()个全振动.使周期偏小
解题思路:(1)小球的偏角α在很小()时,小球的振动才近似看成简谐运动。在摆球经过最低点时开始计时,产生的时间误差较小。
由秒表读出时间:;
周期;
(2)根据单摆的周期公式则有:
A.单摆的振动与摆的质量无关,故A错误;
B.摆的振动周期与振幅无关,故B错误。
C.测量摆长时。只考虑了线长。忽略了小球的半径,则使摆长测量值偏小,根据公式可知,测得出的重力加速度偏小,故C错误;
D.实验中n个全振动误认为(n+1)个全振动,测得周期偏小,则测得的重力加速度偏大。故D正确。
故选:D
答案:(1)低;99.8
(2)D
随堂训练
1、在“用单摆测定重力加速度”的实验中,
(1)测摆长时,若正确测出悬线长和摆球直径,则摆长为 ;
(2)测周期时,当摆球经过 位置(填平衡位置或最高点)时开始计时并计数次,测出经过该位置N次(约次)的时间为t,则周期为 。
答案:(1) (2) 平衡 ;
2、某同学在做“利用单摆测重力加速度”的实验时,先测得摆线长,摆球直径,然后用秒表记录了单摆全振动50次所用的时间,则
(1)他测得的重力加速度___________.(,结果保留三位有效数字)
(2)他测得的g值偏小,可能的原因是( )
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点上,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将49次全振动记为50次
(3)为了提高实验精度,在实验中可改变几次摆线长并测出相应的周期T,从而得到几组与T的数据,再以为横坐标,为纵坐标,将所得数据描点连成直线,并求得该直线的斜率为k,则重力加速度_____________(用k表示).
答案:(1)9.77 (2)B (3)
3、利用单摆测当地重力加速度的实验中
①利用游标卡尺测得金属小球直径如图丁所示,小球直径______;
②甲乙两个学习小组分别利用单摆测量重力加速度。甲组同学采用图甲所示的实验装置;
A.为比较准确地测量出当地重力加速度的数值,除秒表外,在下列器材中,还应该选用______;(用器材前的字母表示)
a.长度接近的细绳
b.长度为左右的细绳
c.直径为的塑料球
d.直径为的铁球
e.最小刻度为的米尺
f.最小刻度为的米尺
B.该组同学先测出悬点到小球球心的距离,然后用秒表测出单摆完成次全振动所用的时间t。请写出重力加速度的表达式______。(用所测物理量表示)
C.在测量摆长后,测量周期时,摆球振动过程中悬点处摆线的固定出现松动,摆长略微变长,这将会导致所测重力加速度的数值______。(选填“偏大”、“偏小”或“不变”)
③乙组同学在图甲所示装置的基础上再增加一个速度传感器,如图乙所示。将摆球拉开一小角度使其做简谐运动,速度传感器记录了摆球振动过程中速度随时间变化的关系,如图丙所示的图线。
A.由图丙可知,该单摆的周期______;
B.更换摆线长度后,多次测量,根据实验数据,利用计算机作出(周期平方-摆长)图线,并根据图线拟合得到方程。由此可以得出当地的重力加速度______,(取,结果保留3位有效数字)
④某同学在实验过程中,摆长没有加小球的半径,其它操作无误,那么他得到的实验图象可能是下列图象中的______。
答案:①22.6
②adf;;偏小
③2.0;9.76
④B
2
