3.3 相似图形 课件(共16张PPT)
文档属性
| 名称 | 3.3 相似图形 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 16:10:57 | ||
图片预览



文档简介
(共16张PPT)
3.3 相似图形
湘教版九年级上册
课前预习
说一说
活动1:知识准备
已知△ABC≌△A′B′C′,若∠A=60°,∠B=40°,则∠C′= 。
活动2:教材导学
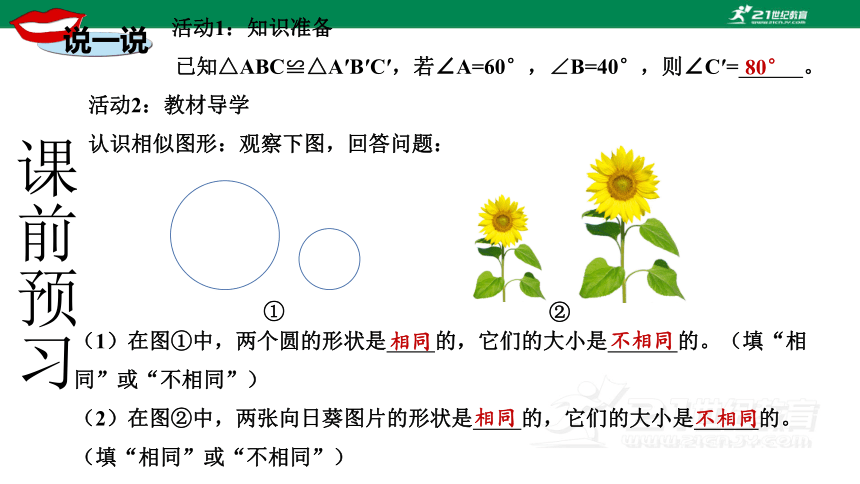
认识相似图形:观察下图,回答问题:
(1)在图①中,两个圆的形状是 的,它们的大小是 的。(填“相同”或“不相同”)
(2)在图②中,两张向日葵图片的形状是 的,它们的大小是 的。(填“相同”或“不相同”)
①
②
80°
相同
不相同
相同
不相同
问题导入
动脑筋
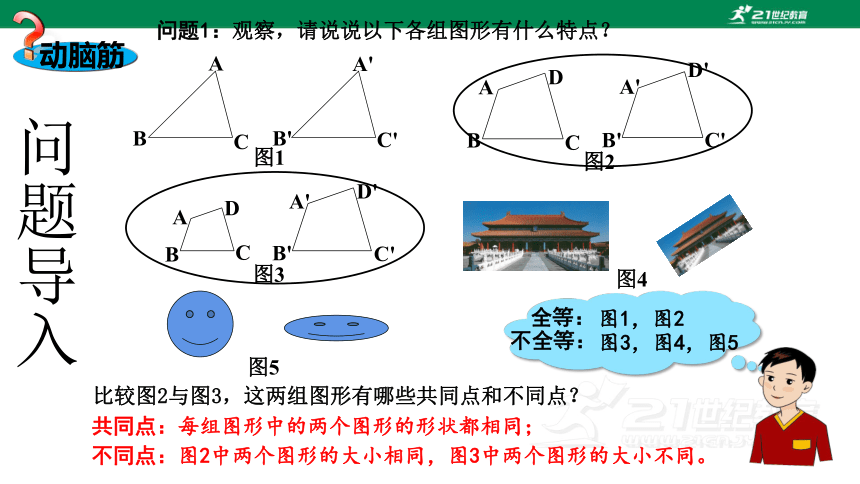
问题1:观察,请说说以下各组图形有什么特点?
比较图2与图3,这两组图形有哪些共同点和不同点?
不同点:图2中两个图形的大小相同,图3中两个图形的大小不同。
A
B
C
A'
B'
C'
图1
A
B
C
D
A'
B'
C'
D'
图2
A'
B'
C'
D'
A
B
C
D
图3
图4
共同点:每组图形中的两个图形的形状都相同;
图5
全等:
不全等:
图1,图2
图3,图4,图5
合作探究
知识点一:相似图形
归纳
相似图形:直观上,把一个图形放大(或缩小)得到的图形与原图形是相似的。
请用自己的语言叙述图形形状相同的本质特征。
图形的形状完全相同,与
图形的大小、位置无关。
说一说
课堂练习
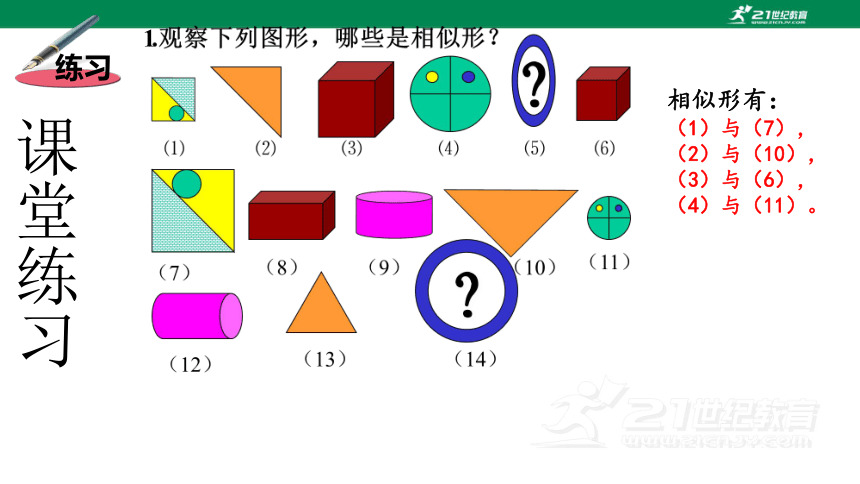
练习
相似形有:
(1)与(7),
(2)与(10),
(3)与(6),
(4)与(11)。
1
课堂练习
练习
2、观察下图的各组图形,哪些是相似图形?哪些不是相似图形?
判定相似图形的方法:
(1)直观法:形状完全相同,一个图形可以由另一个图形放大或缩小得到。全等图形是特殊的相似图形;
(2)测量法:判断两个图形是否相似,可对对应位置的线段进行测量,如果成相同倍数增加(或缩小),且对应角相等,那么这两个图形相似,否则就不相似。
解:(1)(3)(4)是相似图形,(2)不是相似图形。
归纳
合作探究
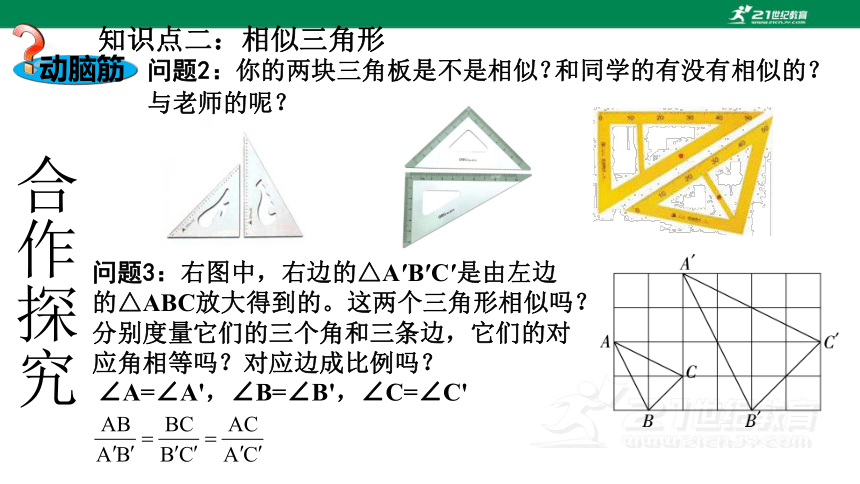
知识点二:相似三角形
动脑筋
和同学的有没有相似的?
与老师的呢?
问题3:右图中,右边的△A′B′C′是由左边的△ABC放大得到的。这两个三角形相似吗?分别度量它们的三个角和三条边,它们的对应角相等吗?对应边成比例吗?
∠A=∠A',∠B=∠B',∠C=∠C'
问题2:你的两块三角板是不是相似?
合作探究
知识点二:相似三角形
注意
定义:三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形。
记法:如果△A′B′C′与△ABC相似,且A′,B′,C′分别与A,B,C对应,记作:△A′B′C′∽△ABC。
相似比:相似三角形的对应边的比,记为k。
(1)用相似符号“∽”表示相似三角形时,应注意对应字母写在对应位置上;
(2)相似比有顺序性,△ABC与△A'B'C'相似比为k时,△A'B'C'与△ABC的相似比为 。相似比k表示第一个三角形的边与第二个三角形的对应边的比值;
(3)特别地,如果相似比k=1,则△ABC≌△A'B'C'。因此,三角形全等是三角形相似的特例。
相似三角形的性质:相似三角形的对应角相等,对应边成比例。
合作探究
举
例
例 如图,已知△ABC∽△A'B'C',且∠A=48°,AB=8,A'B'=4,AC=6。求∠A'的大小和A'C'的长。
解:∵△ABC∽△A′B′C′
又∠A=48°,AB=8,A′B′=4,AC=6
∴∠A′=48°,
即A′C′=3。
∴∠A=∠A′,
课堂练习
练习
如图,已知△A'B'C'∽△ABC,并且A'B'=3cm,AB=2.4cm,BC=1.6cm,∠B=65°,∠C=75°,求B'C'的长以及∠B',∠A'的度数。
解:∵△A′B′C′∽△ABC,∴
再由已知可得:
∴ (cm)
∴∠B′=∠B=65°,∠C′=∠C=75°
∴∠A′=180°-(∠B′+∠C′)=40°
归纳
(1)相似三角形的对应边成比例,对应角相等;
(2)相似三角形中一般相等的角是对应角(如对顶角、公共角);对应角所对的边是对应边,对应边所对的角是对应角。
合作探究
举
例
问题4:类比相似三角形,这两个多边形是否是相似形呢?
对于两个边数相同的多边形,如果它们的对应角相等、对应边成比例,那么这两个多边形叫作相似多边形。
如果四边形ABCD与四边形A1B1C1D1相似,且点A,B,C,D分别与点A1,B1,C1,D1对应。
记作:“四边形ABCD∽四边形A1B1C1D1”。
相似多边形的对应角相等,对应边成比例。
相似多边形的定义:
相似多边形的性质:
相似多边形的对应边的比也叫作相似比。
相似比:
知识点三:相似多边形
归纳
课堂练习
练习
如图,有一块矩形草地,其外围有等宽的小路,其中草地长100m,宽60m,小路宽2m,问内外两个矩形相似吗?
草地
A
B
C
D
A'
B'
C'
D'
解:∵AB=CD=A'B'+2×2=64(m)
BC=AD=B'C'+2×2=104(m)
∴内外两个矩形不相似。
归纳
判定两个多边形相似,必须具备两个条件:一是对应角相等;二是对应边成比例,二者缺一不可。
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
练习
1、放大镜下看到的物体的图形与原图形 相似图形。
(填“是”或“不是”)
2、如果△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为k1,△A′B′C′与△ABC的相似比为k2,则k1与k2的关系是( )
A.k2=k1 B.k1+k2=0 C.k1·k2=-1 D.k1·k2=1
3、如图,已知四边形ABCD∽四边形A′B′C′D′,求∠A的度数及x的值。
是
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.3 相似图形
湘教版九年级上册
课前预习
说一说
活动1:知识准备
已知△ABC≌△A′B′C′,若∠A=60°,∠B=40°,则∠C′= 。
活动2:教材导学
认识相似图形:观察下图,回答问题:
(1)在图①中,两个圆的形状是 的,它们的大小是 的。(填“相同”或“不相同”)
(2)在图②中,两张向日葵图片的形状是 的,它们的大小是 的。(填“相同”或“不相同”)
①
②
80°
相同
不相同
相同
不相同
问题导入
动脑筋
问题1:观察,请说说以下各组图形有什么特点?
比较图2与图3,这两组图形有哪些共同点和不同点?
不同点:图2中两个图形的大小相同,图3中两个图形的大小不同。
A
B
C
A'
B'
C'
图1
A
B
C
D
A'
B'
C'
D'
图2
A'
B'
C'
D'
A
B
C
D
图3
图4
共同点:每组图形中的两个图形的形状都相同;
图5
全等:
不全等:
图1,图2
图3,图4,图5
合作探究
知识点一:相似图形
归纳
相似图形:直观上,把一个图形放大(或缩小)得到的图形与原图形是相似的。
请用自己的语言叙述图形形状相同的本质特征。
图形的形状完全相同,与
图形的大小、位置无关。
说一说
课堂练习
练习
相似形有:
(1)与(7),
(2)与(10),
(3)与(6),
(4)与(11)。
1
课堂练习
练习
2、观察下图的各组图形,哪些是相似图形?哪些不是相似图形?
判定相似图形的方法:
(1)直观法:形状完全相同,一个图形可以由另一个图形放大或缩小得到。全等图形是特殊的相似图形;
(2)测量法:判断两个图形是否相似,可对对应位置的线段进行测量,如果成相同倍数增加(或缩小),且对应角相等,那么这两个图形相似,否则就不相似。
解:(1)(3)(4)是相似图形,(2)不是相似图形。
归纳
合作探究
知识点二:相似三角形
动脑筋
和同学的有没有相似的?
与老师的呢?
问题3:右图中,右边的△A′B′C′是由左边的△ABC放大得到的。这两个三角形相似吗?分别度量它们的三个角和三条边,它们的对应角相等吗?对应边成比例吗?
∠A=∠A',∠B=∠B',∠C=∠C'
问题2:你的两块三角板是不是相似?
合作探究
知识点二:相似三角形
注意
定义:三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形。
记法:如果△A′B′C′与△ABC相似,且A′,B′,C′分别与A,B,C对应,记作:△A′B′C′∽△ABC。
相似比:相似三角形的对应边的比,记为k。
(1)用相似符号“∽”表示相似三角形时,应注意对应字母写在对应位置上;
(2)相似比有顺序性,△ABC与△A'B'C'相似比为k时,△A'B'C'与△ABC的相似比为 。相似比k表示第一个三角形的边与第二个三角形的对应边的比值;
(3)特别地,如果相似比k=1,则△ABC≌△A'B'C'。因此,三角形全等是三角形相似的特例。
相似三角形的性质:相似三角形的对应角相等,对应边成比例。
合作探究
举
例
例 如图,已知△ABC∽△A'B'C',且∠A=48°,AB=8,A'B'=4,AC=6。求∠A'的大小和A'C'的长。
解:∵△ABC∽△A′B′C′
又∠A=48°,AB=8,A′B′=4,AC=6
∴∠A′=48°,
即A′C′=3。
∴∠A=∠A′,
课堂练习
练习
如图,已知△A'B'C'∽△ABC,并且A'B'=3cm,AB=2.4cm,BC=1.6cm,∠B=65°,∠C=75°,求B'C'的长以及∠B',∠A'的度数。
解:∵△A′B′C′∽△ABC,∴
再由已知可得:
∴ (cm)
∴∠B′=∠B=65°,∠C′=∠C=75°
∴∠A′=180°-(∠B′+∠C′)=40°
归纳
(1)相似三角形的对应边成比例,对应角相等;
(2)相似三角形中一般相等的角是对应角(如对顶角、公共角);对应角所对的边是对应边,对应边所对的角是对应角。
合作探究
举
例
问题4:类比相似三角形,这两个多边形是否是相似形呢?
对于两个边数相同的多边形,如果它们的对应角相等、对应边成比例,那么这两个多边形叫作相似多边形。
如果四边形ABCD与四边形A1B1C1D1相似,且点A,B,C,D分别与点A1,B1,C1,D1对应。
记作:“四边形ABCD∽四边形A1B1C1D1”。
相似多边形的对应角相等,对应边成比例。
相似多边形的定义:
相似多边形的性质:
相似多边形的对应边的比也叫作相似比。
相似比:
知识点三:相似多边形
归纳
课堂练习
练习
如图,有一块矩形草地,其外围有等宽的小路,其中草地长100m,宽60m,小路宽2m,问内外两个矩形相似吗?
草地
A
B
C
D
A'
B'
C'
D'
解:∵AB=CD=A'B'+2×2=64(m)
BC=AD=B'C'+2×2=104(m)
∴内外两个矩形不相似。
归纳
判定两个多边形相似,必须具备两个条件:一是对应角相等;二是对应边成比例,二者缺一不可。
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
练习
1、放大镜下看到的物体的图形与原图形 相似图形。
(填“是”或“不是”)
2、如果△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为k1,△A′B′C′与△ABC的相似比为k2,则k1与k2的关系是( )
A.k2=k1 B.k1+k2=0 C.k1·k2=-1 D.k1·k2=1
3、如图,已知四边形ABCD∽四边形A′B′C′D′,求∠A的度数及x的值。
是
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
