点和圆的位置关系

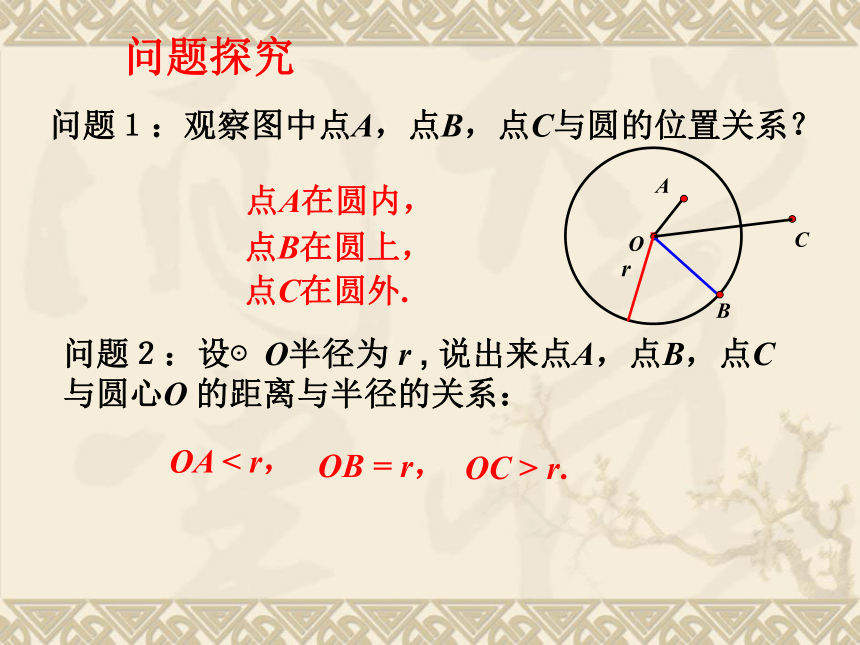
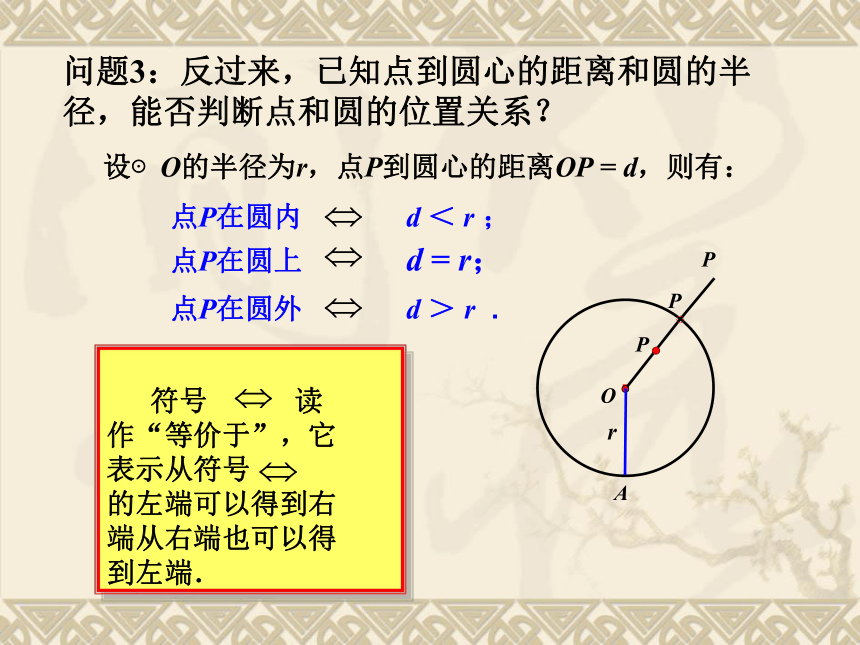
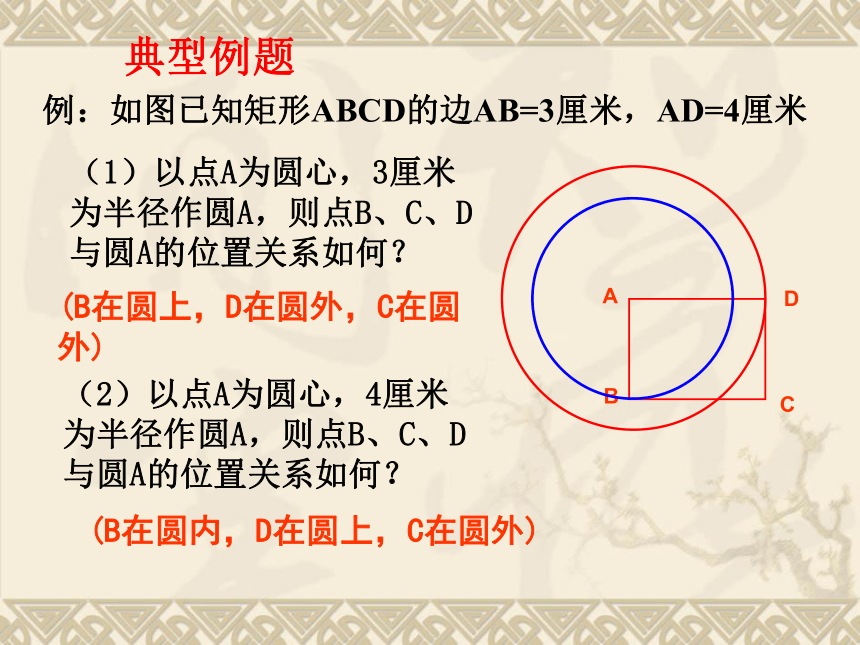
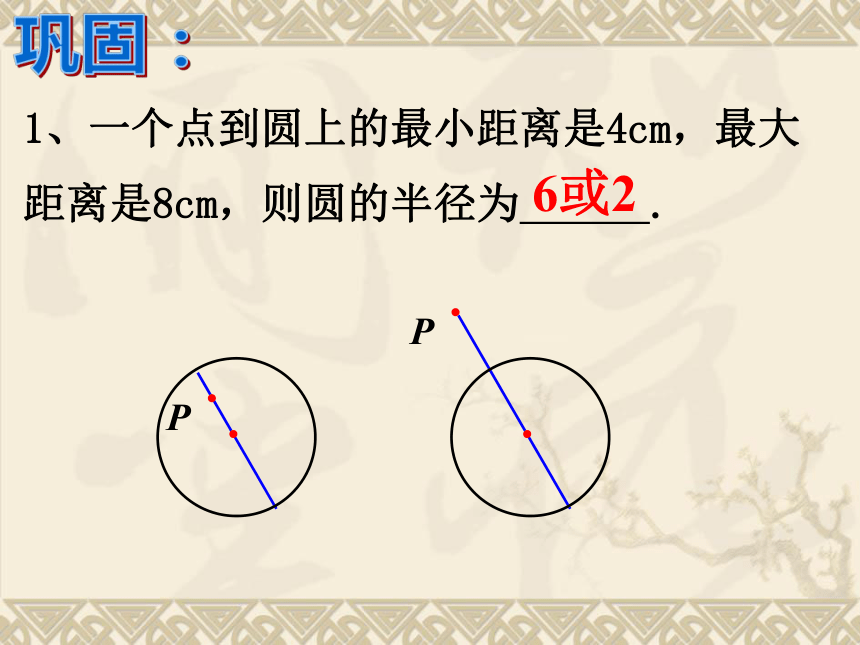
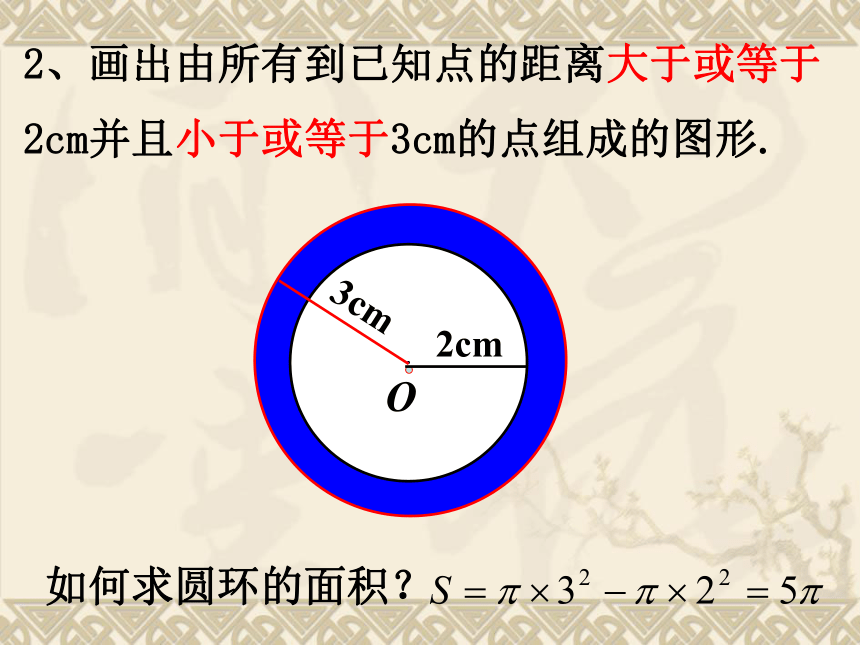
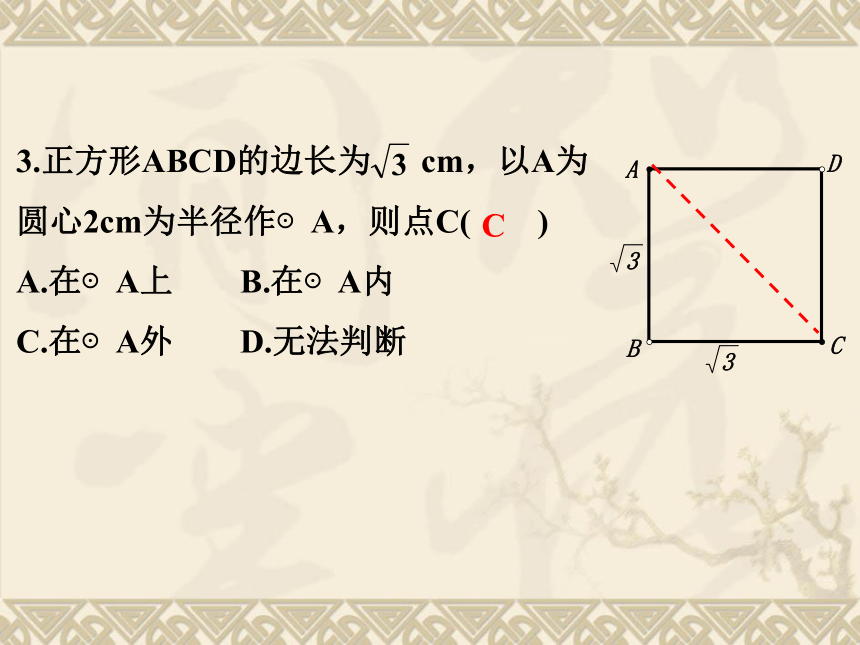
课件24张PPT。24.2.1.点和圆的位置关系射击靶示意图百步穿杨生活中的数学如果箭看成点，箭靶看成圆，那么上面情境反映了点与圆的位置关系。r问题２：设⊙O半径为 r , 说出来点A，点B，点C与圆心O 的距离与半径的关系：·COABOC > r.问题１：观察图中点A，点B，点C与圆的位置关系？点C在圆外.点A在圆内，点B在圆上，OA < r，OB = r，问题探究设⊙O的半径为r，点P到圆心的距离OP = d，则有：点P在圆上 d = r；点P在圆外 d ＞ r . 点P在圆内 d ＜ r ； r·OA问题3：反过来，已知点到圆心的距离和圆的半径，能否判断点和圆的位置关系？PPP例：如图已知矩形ABCD的边AB=3厘米，AD=4厘米典型例题（1）以点A为圆心，3厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？(B在圆上，D在圆外，C在圆外)（2）以点A为圆心，4厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？(B在圆内，D在圆上，C在圆外)（3）以点A为圆心，5厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？(B在圆内，D在圆内，C在圆上)1、一个点到圆上的最小距离是4cm，最大距离是8cm，则圆的半径为 .巩固：6或22、画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.·2cm3cmO如何求圆环的面积？C探究二：
问题1：过已知点A可以作几个圆？●A 过一点可以做 无数个圆 问题2：过已知点A、B可以作几个圆？它们的圆心分布有什么特点？ 过两点可以作无数个圆，
它们的圆心都在线段AB的垂直平分线上。O不在同一直线上的三个点确定一个圆问题3：要经过不在同一直线上的三点作几个圆，如何确定这个圆的圆心？ 经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆，外接圆的圆心叫做这个三角形的外心，外心是三角形三边垂直平分线的交点。 外心到三角形三个顶点的距离相等。 操作：由图可知，锐角三角形的外心在三角形内，那钝角三角形、直角三角形的外心呢？画图说明。 归纳：锐角三角形的外心在三角形内;直角三角形的外心在斜边中点；钝角三角形的外心在三角形外。1. ①⊙O叫做△ABC的________， △ABC叫做⊙O的____________.到三角形三个顶点的距离相等。②三角形的外心：
定义：●O外接圆　内接三角形　三角形外接圆的圆心叫做三角形的外心。作图：三角形三边中垂线的交点。性质： 1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( ) 2、若一个三角形的外心在一边上，则此三角形的 形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形√××√B思考： 如图，CD所在的直线垂直平分线段AB，怎样用这样的工具找到圆形工件的圆心．DO∵A、B两点在圆上，所以圆心必与A、B两点的距离相等，又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上，∴圆心在CD所在的直线上，因此可以做任意两条直径，它们的交点为圆心. 例1．某地出土一明代残破圆形镜子，如图所示．为复制该镜子确定其圆心和半径，请在图中用直尺和圆规画出镜子的圆心．圆心一定在弦的垂直平分线上1.如图，已知等边三角形ABC中，
边长为6cm，求它的外接圆半径.2.如图，已知 Rt⊿ABC 中 ，若 AC=12cm，BC=5cm，求的外接圆半径. 思考：过同一直线上的三点可以作圆吗？过同一直线上的三点不能作圆。先假设命题的结论不成立，然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾)，由矛盾判定假设不正确，从而得到原命题成立，这种方法叫做反证法．步骤：（1）假设命题的结论不成立
（2）推理得出矛盾
（3）结论成立反证法证明：过同一直线上的三点不能作圆证明：(1)如图，假设过同一条直线l上三点A、B、C可以作一个圆，
(2)设这个圆的圆心为P，那么点P既在线段AB的垂直平分线l1上，又在线段BC的垂直平分线l2上，即点P为l1与l2的交点，
(3)而l1⊥l，l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾，所以过同一条直线上的三点不能作圆．思考：任意四个点是不是可以作一个圆？请举例说明. 不一定1. 四点在一条直线上不能作圆；3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.ABCDABCDABCDABCD2. 三点在同一直线上, 另一点不在这条直线上不能作圆；对角互补的四边形的四个顶点在同一个圆上小结:1.点与圆的位置关系2.不在同一条直线上的三个点确定一个圆。3.外心4.反证法