14.1.4整式的乘法
图片预览





文档简介
课件18张PPT。14.1.4整式的乘法
3.多项式与多项式相乘学习目标:
1、经历探索多项式乘法法则的过程,理解多项式乘法法则。
2、灵活运用多项式乘以多项式的运算法则。
学习重点:
多项式与多项式相乘.
学习难点:
探索多项式乘法的法则,注意多项式乘法的运算中“漏乘”、“负号”的问题.1、单项式与单项式相乘的法则? ①2x2·(-4xy)=
②(-2x2)·(-3xy2)=
③(-9a2 b3)·(8ab2) = -72a3 b5 单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.-8x3y6x3y2单项式与多项式相乘的法则:2: 单项式与多项式相乘,就是用单项式去乘
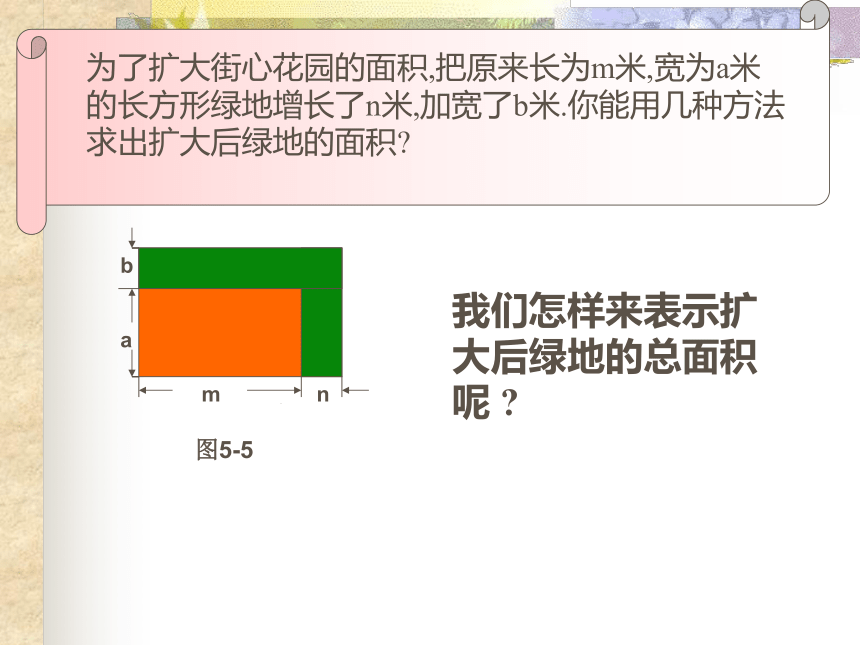
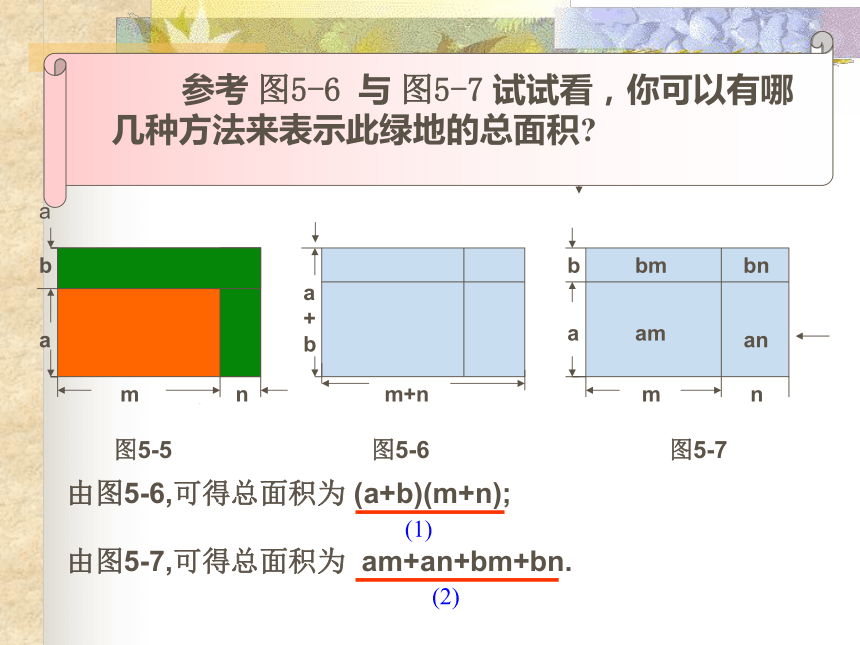
再把所得的积相加多项式的每一项amn图5-5b我们怎样来表示扩大后绿地的总面积呢 ?a+bm+nbabmammaamn图5-5图5-6图5-7由图5-6,可得总面积为 (a+b)(m+n);由图5-7,可得总面积为 am+an+bm+bn.bnannb(1) (2) anbm a+babanbmam + an + bm + bn=+++由此,我们可以得到什么结论呢?(a+b)(m+n)多项式与多项式相乘的法则:即(a+b)(m+n)=多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.=am+an+bm+bn am+an+bm+bn(1)(x+y)(a+2b); (2) (3x-1)(x+3)注意:1、两项相乘时,先定符号。所得积的符号由这两项的符号来确定:负负得正,一正一负得负。
2、最后的结果要合并同类项. 例1 计算:
解:原式解:原式注意:
1、必须做到不重复,不遗漏.2、注意确定积中每一项的符号.
3、结果应化为最简式
{合并同类项}. (1)(3x+1)(x?2);1、计算:(2)(x-8y)(x?y) ;=3x·x+3x·(-2)+1·x+1× (?2)=3x2-6x+x?2=3x2-5x?2=x2-xy?8xy+8y2=x2?9xy+8y2注 意 !1.计算(a+b)2应该这样做:
(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
切记 一般情况下
(a+b)2不等a2+b2 .例2 先化简,再求值:解:原式=3xy-9x2-2y2+6xy-(6x2+2xy-3xy-y2) =3xy-9x2-2y2+6xy-6x2-2xy+3xy+y2 =-15x2+10xy-y2-15x2+10xy-y2练习:(1) (2x+1)(x+3) ;(2) (m+n)(a+b+c)练习:(1) (2a+b)2;(2) (x+y)(2x–y) 1、漏乘 需要注意的几个问题2、符号问题 3、最后结果应化成最简形式。谢谢大家!祝大家马到成功!
3.多项式与多项式相乘学习目标:
1、经历探索多项式乘法法则的过程,理解多项式乘法法则。
2、灵活运用多项式乘以多项式的运算法则。
学习重点:
多项式与多项式相乘.
学习难点:
探索多项式乘法的法则,注意多项式乘法的运算中“漏乘”、“负号”的问题.1、单项式与单项式相乘的法则? ①2x2·(-4xy)=
②(-2x2)·(-3xy2)=
③(-9a2 b3)·(8ab2) = -72a3 b5 单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.-8x3y6x3y2单项式与多项式相乘的法则:2: 单项式与多项式相乘,就是用单项式去乘
再把所得的积相加多项式的每一项amn图5-5b我们怎样来表示扩大后绿地的总面积呢 ?a+bm+nbabmammaamn图5-5图5-6图5-7由图5-6,可得总面积为 (a+b)(m+n);由图5-7,可得总面积为 am+an+bm+bn.bnannb(1) (2) anbm a+babanbmam + an + bm + bn=+++由此,我们可以得到什么结论呢?(a+b)(m+n)多项式与多项式相乘的法则:即(a+b)(m+n)=多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.=am+an+bm+bn am+an+bm+bn(1)(x+y)(a+2b); (2) (3x-1)(x+3)注意:1、两项相乘时,先定符号。所得积的符号由这两项的符号来确定:负负得正,一正一负得负。
2、最后的结果要合并同类项. 例1 计算:
解:原式解:原式注意:
1、必须做到不重复,不遗漏.2、注意确定积中每一项的符号.
3、结果应化为最简式
{合并同类项}. (1)(3x+1)(x?2);1、计算:(2)(x-8y)(x?y) ;=3x·x+3x·(-2)+1·x+1× (?2)=3x2-6x+x?2=3x2-5x?2=x2-xy?8xy+8y2=x2?9xy+8y2注 意 !1.计算(a+b)2应该这样做:
(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
切记 一般情况下
(a+b)2不等a2+b2 .例2 先化简,再求值:解:原式=3xy-9x2-2y2+6xy-(6x2+2xy-3xy-y2) =3xy-9x2-2y2+6xy-6x2-2xy+3xy+y2 =-15x2+10xy-y2-15x2+10xy-y2练习:(1) (2x+1)(x+3) ;(2) (m+n)(a+b+c)练习:(1) (2a+b)2;(2) (x+y)(2x–y) 1、漏乘 需要注意的几个问题2、符号问题 3、最后结果应化成最简形式。谢谢大家!祝大家马到成功!
