华师大版数学九年级上册 23.4.中位线 课件(共14张PPT)
文档属性
| 名称 | 华师大版数学九年级上册 23.4.中位线 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 16:25:10 | ||
图片预览





文档简介
(共14张PPT)
23.4. 中位线
第23章 图形的相似
复习导入
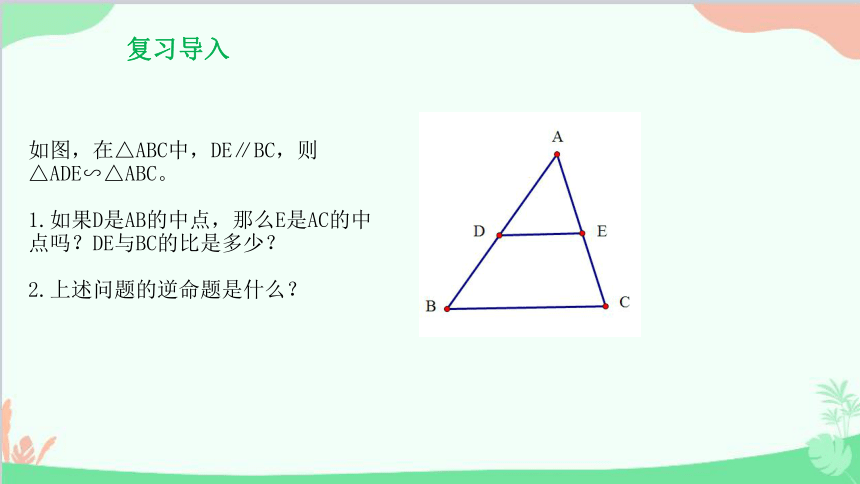
如图,在△ABC中,DE∥BC,则△ADE∽△ABC。
1.如果D是AB的中点,那么E是AC的中点吗?DE与BC的比是多少?
2.上述问题的逆命题是什么?
探索新知
逆命题:如果D、E分别是AB、AC边的中点,那么DE∥BC,∴DE= BC.
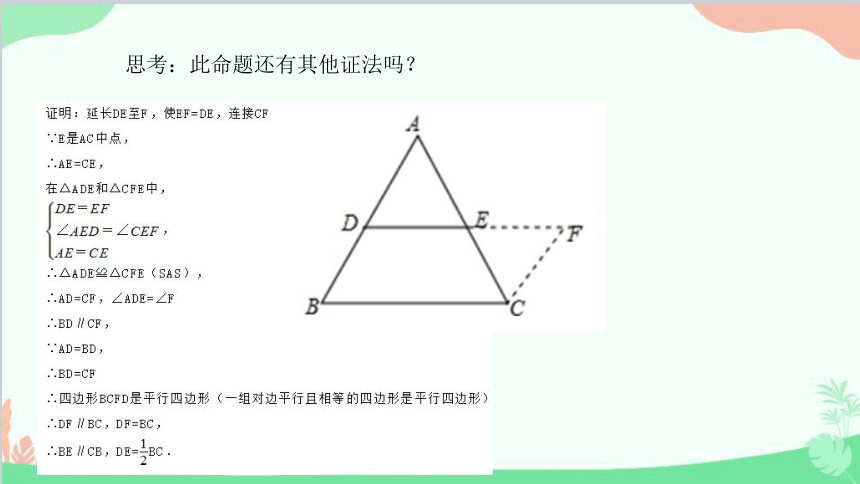
思考:此命题还有其他证法吗?
归纳
(1)我们把连结三角形两边中点的线段叫做三角形的中位线。
(2)三角形的中位线平行于第三边,并且等于第三边的一半。
应用
应用拓展
在例2中,作另外两条三角形的中线,是否也有这个结论?
(学生讨论,总结如下)
三角形三边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的 ?
巩固练习
答案:1.3 90°.
归纳小结
1.三角形中位线与中线的区别。
2.中点四边形一定是平行四边形,判断他是不是某一特殊平行四边形,只需要看原四边形对角线是否垂直或相等。
数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深。
——高斯
谢谢大家!
/
A
D
E
B
C
证明:延长DE至F,使EF=DE,连接CF
.E是AC中点,
∴.AE=CE,
在△ADE和△CFE中,
(DE-EF
∠AED=∠CEF·
LAE=CE
.∴.△ADE≌△CFE(SAS),
∴.AD=CF,∠ADE=∠F
.'.BD CF,
'.'AD=BD,
.∴.BD=CF
'.四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
.∴.DF∥BC,DF=BC,
.∴.BE∥CB,DE=5BC.
证
连结ED.
D、E分别是边BC、AB的中点,
DE/4C,光-号(三角形的中位线平行于第
三边,并且等于第三边的一半),
△ACGO△DEG,
GE
GD
DE
1
CC
GA
AC
2
GE
GD
1
CE
AD
3
1.如图,在△ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、CF相交于点O,
AB=6,BC=I0,AC=8.试求出线段DE、OA、OF的长及∠EDF的大小.(结采保
留根号)
B
D
(第1题)
2.求证:顺次连结四边形各边的中,点所得的四边形是平行四边形.
23.4. 中位线
第23章 图形的相似
复习导入
如图,在△ABC中,DE∥BC,则△ADE∽△ABC。
1.如果D是AB的中点,那么E是AC的中点吗?DE与BC的比是多少?
2.上述问题的逆命题是什么?
探索新知
逆命题:如果D、E分别是AB、AC边的中点,那么DE∥BC,∴DE= BC.
思考:此命题还有其他证法吗?
归纳
(1)我们把连结三角形两边中点的线段叫做三角形的中位线。
(2)三角形的中位线平行于第三边,并且等于第三边的一半。
应用
应用拓展
在例2中,作另外两条三角形的中线,是否也有这个结论?
(学生讨论,总结如下)
三角形三边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的 ?
巩固练习
答案:1.3 90°.
归纳小结
1.三角形中位线与中线的区别。
2.中点四边形一定是平行四边形,判断他是不是某一特殊平行四边形,只需要看原四边形对角线是否垂直或相等。
数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深。
——高斯
谢谢大家!
/
A
D
E
B
C
证明:延长DE至F,使EF=DE,连接CF
.E是AC中点,
∴.AE=CE,
在△ADE和△CFE中,
(DE-EF
∠AED=∠CEF·
LAE=CE
.∴.△ADE≌△CFE(SAS),
∴.AD=CF,∠ADE=∠F
.'.BD CF,
'.'AD=BD,
.∴.BD=CF
'.四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
.∴.DF∥BC,DF=BC,
.∴.BE∥CB,DE=5BC.
证
连结ED.
D、E分别是边BC、AB的中点,
DE/4C,光-号(三角形的中位线平行于第
三边,并且等于第三边的一半),
△ACGO△DEG,
GE
GD
DE
1
CC
GA
AC
2
GE
GD
1
CE
AD
3
1.如图,在△ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、CF相交于点O,
AB=6,BC=I0,AC=8.试求出线段DE、OA、OF的长及∠EDF的大小.(结采保
留根号)
B
D
(第1题)
2.求证:顺次连结四边形各边的中,点所得的四边形是平行四边形.
