华师大版数学九年级上册 24.4 解直角三角形2 第1课时 课件(共13张PPT)
文档属性
| 名称 | 华师大版数学九年级上册 24.4 解直角三角形2 第1课时 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 782.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 16:27:58 | ||
图片预览



文档简介
(共13张PPT)
25.3.1解直角三角形
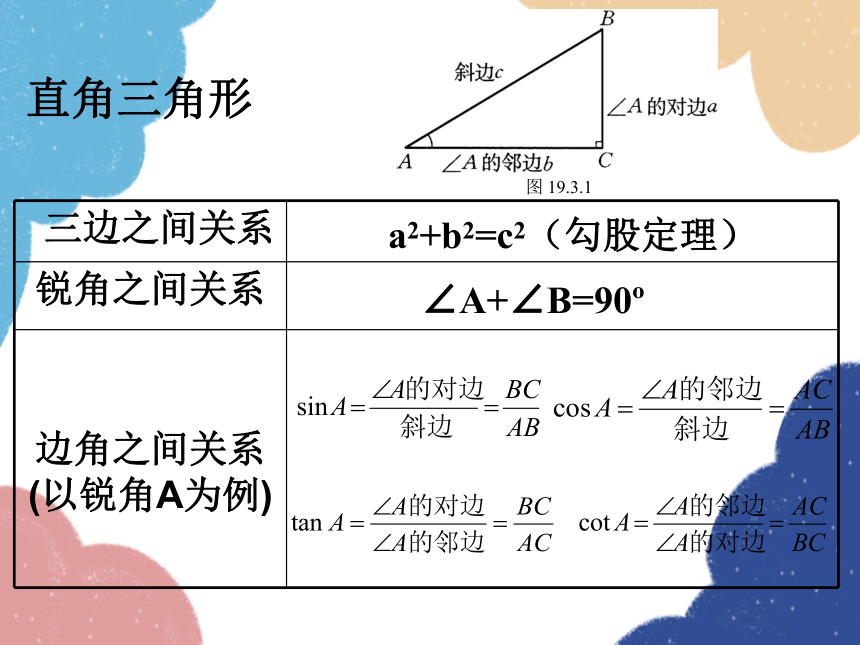
直角三角形
三边之间关系
锐角之间关系
边角之间关系
(以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
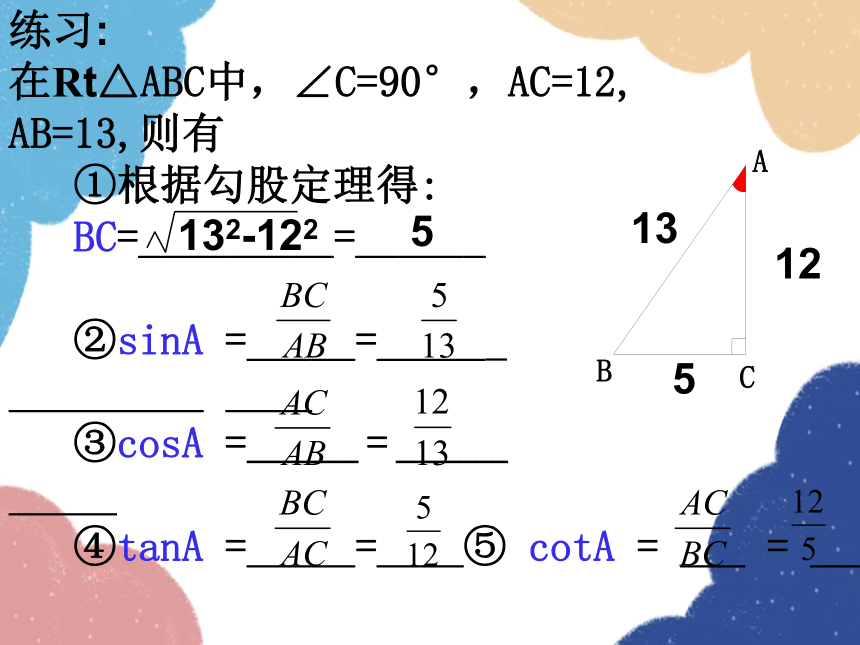
练习:
在Rt△ABC中,∠C=90°,AC=12,
AB=13,则有
①根据勾股定理得:
BC=_________=______
②sinA =_____=_____
③cosA =_______ = _______
④tanA =_____=____⑤ cotA = ___ = ___
5
132-122
12
13
5
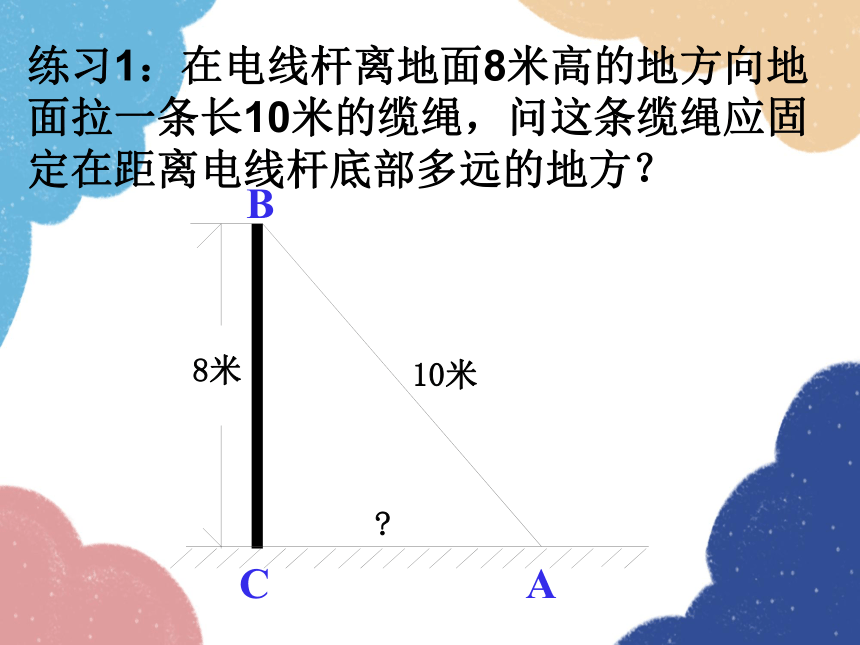
练习1:在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
B
C
A
1、在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三形 ;
3、在直角三角形中,如果已知两条边的长度,那么就可利用勾股定理求出另外的一条边。
2、在解决实际问题时,应“先画图,再求解”;
概括
4、在直角三角形中,如果已知两条边的长
度,能否求出另外两个锐角?
虎门威远炮台
虎门威远的东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求:
(1)敌舰C与炮台A的距离;
(2)敌舰C与炮台B的距离.
(精确到1米)
(1)在直角三角形中,已知一条边
和一个锐角,可利用三角函数来求另外
的边 .
注意:
(2)解直角三角形过程中,常会遇
到近似计算,本书除特别说明外,边长
保留四个有效数字,角度精确到
练习2:海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求
(1)从A处到B处的距离;
(2)灯塔Q到B处的距离
(画出图形后计算,
精确到 0.1 海里)
10. (2010 湖北省孝感市) 如图,一艘船向正北航行,在处看到灯塔在船的北偏东的方向上,航行12海里到达点.在处看到灯塔在船的北偏东的方向上.此船继续沿正北方向航行过程中距灯塔的最近距离是多少海里?
60°
30°
S
B
A
北
南
西
东
30. (2010 四川省内江市) 为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造.如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点A再在河这边沿河取两点B,C,在点B处测得点A在北偏东方向上,在点C处测得点A在西北方向上,量得长为200米.请你求出该河段的宽度(结果保留根号).
20. (2010 辽宁省本溪市) 一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东45°方向.
(1)求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里?(结果精确到个位,参考数据:≈1.73)
A
N
M
北
东
小结
①定义:在直角三角形中,由已 知元素求出未知元素的过程,叫做解直角三角形;
②在解决实际问题时,应“先画图,再求解”;
③解直角三角形,只有下面两种情况可解:
(1)已知两条边;
(2)已知一条边和一个锐角。
25.3.1解直角三角形
直角三角形
三边之间关系
锐角之间关系
边角之间关系
(以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
练习:
在Rt△ABC中,∠C=90°,AC=12,
AB=13,则有
①根据勾股定理得:
BC=_________=______
②sinA =_____=_____
③cosA =_______ = _______
④tanA =_____=____⑤ cotA = ___ = ___
5
132-122
12
13
5
练习1:在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
B
C
A
1、在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三形 ;
3、在直角三角形中,如果已知两条边的长度,那么就可利用勾股定理求出另外的一条边。
2、在解决实际问题时,应“先画图,再求解”;
概括
4、在直角三角形中,如果已知两条边的长
度,能否求出另外两个锐角?
虎门威远炮台
虎门威远的东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求:
(1)敌舰C与炮台A的距离;
(2)敌舰C与炮台B的距离.
(精确到1米)
(1)在直角三角形中,已知一条边
和一个锐角,可利用三角函数来求另外
的边 .
注意:
(2)解直角三角形过程中,常会遇
到近似计算,本书除特别说明外,边长
保留四个有效数字,角度精确到
练习2:海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求
(1)从A处到B处的距离;
(2)灯塔Q到B处的距离
(画出图形后计算,
精确到 0.1 海里)
10. (2010 湖北省孝感市) 如图,一艘船向正北航行,在处看到灯塔在船的北偏东的方向上,航行12海里到达点.在处看到灯塔在船的北偏东的方向上.此船继续沿正北方向航行过程中距灯塔的最近距离是多少海里?
60°
30°
S
B
A
北
南
西
东
30. (2010 四川省内江市) 为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造.如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点A再在河这边沿河取两点B,C,在点B处测得点A在北偏东方向上,在点C处测得点A在西北方向上,量得长为200米.请你求出该河段的宽度(结果保留根号).
20. (2010 辽宁省本溪市) 一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东45°方向.
(1)求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里?(结果精确到个位,参考数据:≈1.73)
A
N
M
北
东
小结
①定义:在直角三角形中,由已 知元素求出未知元素的过程,叫做解直角三角形;
②在解决实际问题时,应“先画图,再求解”;
③解直角三角形,只有下面两种情况可解:
(1)已知两条边;
(2)已知一条边和一个锐角。
