2022-2023学年湘教版数学八年级上册 第5章 5.3二次根式的加法和减法 课件(共30张PPT)
文档属性
| 名称 | 2022-2023学年湘教版数学八年级上册 第5章 5.3二次根式的加法和减法 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 17:55:56 | ||
图片预览










文档简介
(共30张PPT)
二次根式的加法和减法
做一做
计算:
动脑筋
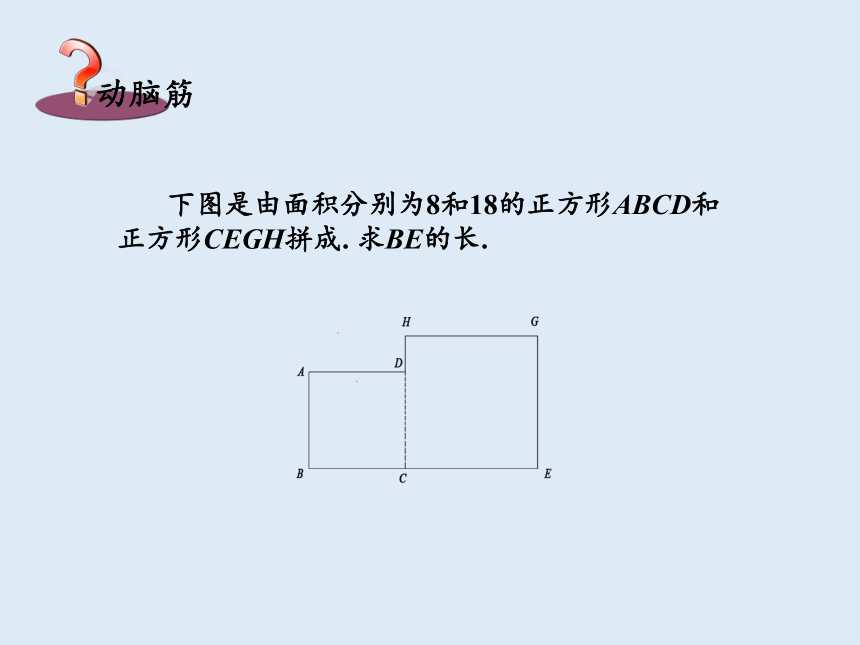
下图是由面积分别为8和18的正方形ABCD和
正方形CEGH拼成. 求BE的长.
因为正方形ABCD 和CEGH的边长分别为 和 ,
所以BE的长度为
(化成最简二次根式)
(分配律)
在进行二次根式的加减运算时, 通常应先将每个
二次根式化简,然后再将被开方数相同的二次根式的
系数相加减,但被开方数不变.
举
例
例1 计算:
解
二次根式的加减与
合并同类项类似.
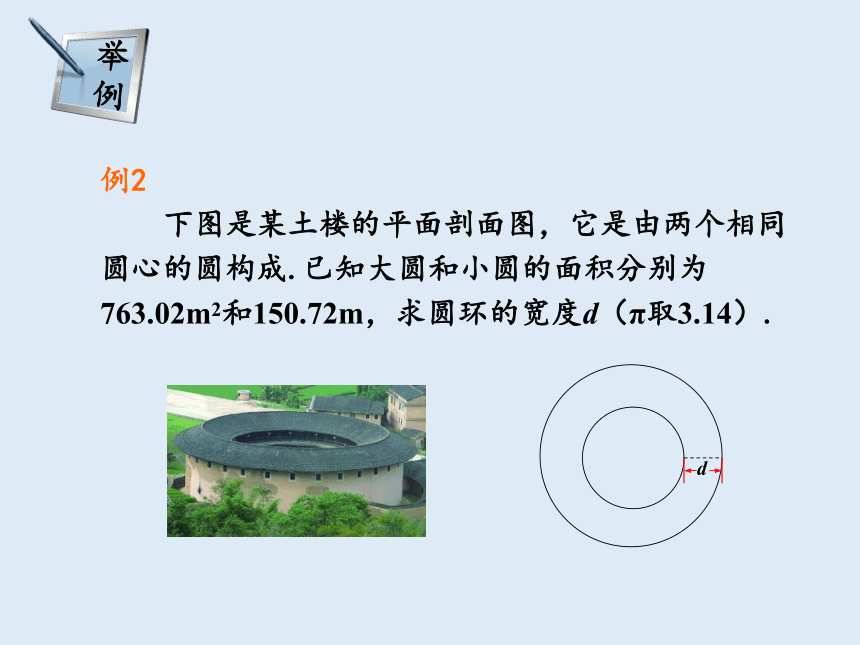
例2
下图是某土楼的平面剖面图,它是由两个相同圆心的圆构成.已知大圆和小圆的面积分别为763.02m2和150.72m,求圆环的宽度d(π取3.14).
举
例
d
解
设大圆和小圆的半径分别为R,r,面积分别为 , ,由 ,
可知
则
答:圆环的宽度为
1. 计算:
练习
2. 计算:
动脑筋
甲、乙两个城市间计划修建一条城际铁路,
其中有一段路基的横断面设计为上底宽 ,
下底宽 ,高 的梯形,这段路基长500m,那么这段路基的土石方为多少立方米呢(路基的土石方即等于路基的体积)?
路基的土石方等于路基横断面面积乘以路基的
长度,所以,这段路基的土石方为:
即这段路基的土石方为
从上面的解答过程可以看到,二次根式的
混合运算是根据实数的运算律进行的.
举
例
例3 计算:
从例3可以看到,二次根式相乘,与多项式
的乘法相类似,我们可以利用多项式的乘法公式,
对某些二次根式的乘法进行简便运算.
例4 计算:
举
例
从例4的第(1)小题的结果受到启发,把分子与分母都乘以 ,就可以使分母变成1.
动脑筋
如何计算 ?
举
例
例5 计算:
解
1. 计算:
练习
2. 计算:
小结与复习
1. 二次根式 在实数范围内有意义的条件是什么?
2. 二次根式有哪些性质?
4. 如何进行二次根式的加、减、乘、除运算?
举例说明什么叫最简二次根式,试写出一个二次
根式并将它化简.
加、减、乘、除运算
二次根式
性质
最简二次根式
积的算术平方根的性质:
商的算术平方根的性质:
本章知识结构
1. 二次根式 在实数范围内有意义,必须满足 .
学习了二次根式以后,代数式可看成是把数和表示
数的字母用运算符号(加、减、乘、除、乘方和开方)
连接而成的式子.
积与商的算数平方根性质公式从右至左地使用,
可以进行二次根式的乘、除运算.
3.
实数的运算律在二次根式的加、减、乘、除运算
中仍然成立.
注意
谢 谢
二次根式的加法和减法
做一做
计算:
动脑筋
下图是由面积分别为8和18的正方形ABCD和
正方形CEGH拼成. 求BE的长.
因为正方形ABCD 和CEGH的边长分别为 和 ,
所以BE的长度为
(化成最简二次根式)
(分配律)
在进行二次根式的加减运算时, 通常应先将每个
二次根式化简,然后再将被开方数相同的二次根式的
系数相加减,但被开方数不变.
举
例
例1 计算:
解
二次根式的加减与
合并同类项类似.
例2
下图是某土楼的平面剖面图,它是由两个相同圆心的圆构成.已知大圆和小圆的面积分别为763.02m2和150.72m,求圆环的宽度d(π取3.14).
举
例
d
解
设大圆和小圆的半径分别为R,r,面积分别为 , ,由 ,
可知
则
答:圆环的宽度为
1. 计算:
练习
2. 计算:
动脑筋
甲、乙两个城市间计划修建一条城际铁路,
其中有一段路基的横断面设计为上底宽 ,
下底宽 ,高 的梯形,这段路基长500m,那么这段路基的土石方为多少立方米呢(路基的土石方即等于路基的体积)?
路基的土石方等于路基横断面面积乘以路基的
长度,所以,这段路基的土石方为:
即这段路基的土石方为
从上面的解答过程可以看到,二次根式的
混合运算是根据实数的运算律进行的.
举
例
例3 计算:
从例3可以看到,二次根式相乘,与多项式
的乘法相类似,我们可以利用多项式的乘法公式,
对某些二次根式的乘法进行简便运算.
例4 计算:
举
例
从例4的第(1)小题的结果受到启发,把分子与分母都乘以 ,就可以使分母变成1.
动脑筋
如何计算 ?
举
例
例5 计算:
解
1. 计算:
练习
2. 计算:
小结与复习
1. 二次根式 在实数范围内有意义的条件是什么?
2. 二次根式有哪些性质?
4. 如何进行二次根式的加、减、乘、除运算?
举例说明什么叫最简二次根式,试写出一个二次
根式并将它化简.
加、减、乘、除运算
二次根式
性质
最简二次根式
积的算术平方根的性质:
商的算术平方根的性质:
本章知识结构
1. 二次根式 在实数范围内有意义,必须满足 .
学习了二次根式以后,代数式可看成是把数和表示
数的字母用运算符号(加、减、乘、除、乘方和开方)
连接而成的式子.
积与商的算数平方根性质公式从右至左地使用,
可以进行二次根式的乘、除运算.
3.
实数的运算律在二次根式的加、减、乘、除运算
中仍然成立.
注意
谢 谢
同课章节目录
