2022-2023学年湘教版数学八年级上册 第4章 本章复习与测试 课件(共29张PPT)
文档属性
| 名称 | 2022-2023学年湘教版数学八年级上册 第4章 本章复习与测试 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 18:03:40 | ||
图片预览







文档简介
(共29张PPT)
第四章 一元一次不等式(组)
复习课件
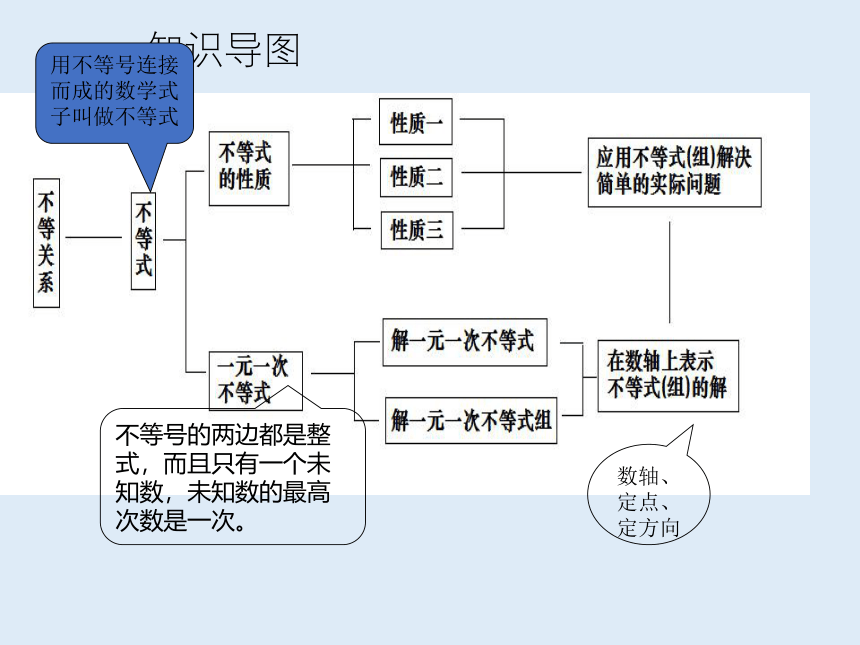
一、知识导图
不等号的两边都是整式,而且只有一个未知数,未知数的最高次数是一次。
数轴、定点、定方向
用不等号连接而成的数学式子叫做不等式
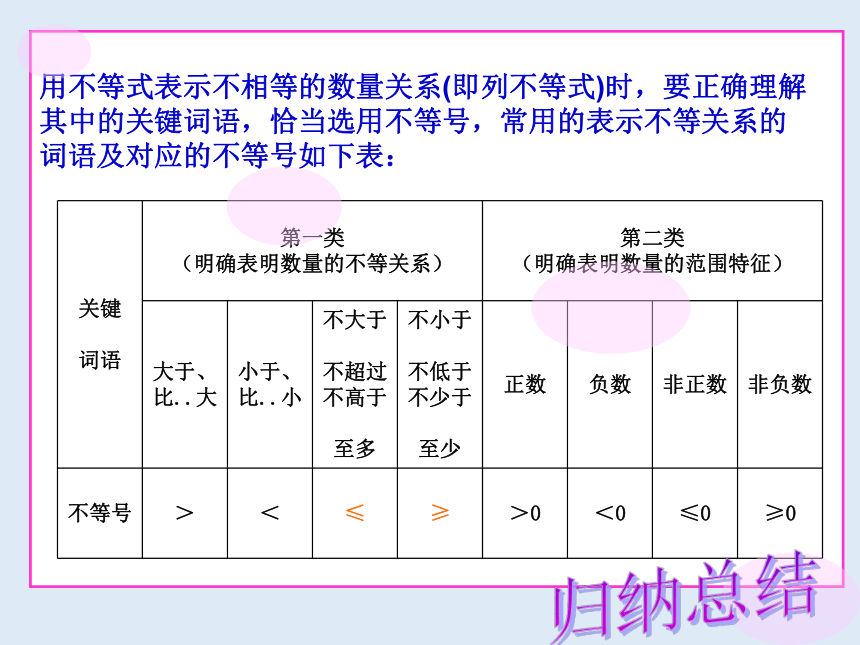
关键 词语 第一类 (明确表明数量的不等关系) 第二类 (明确表明数量的范围特征)
大于、 比..大 小于、 比..小 不大于 不超过 不高于 至多 不小于 不低于 不少于 至少 正数 负数 非正数 非负数
不等号 > < ≤ ≥ >0 <0 ≤0 ≥0
用不等式表示不相等的数量关系(即列不等式)时,要正确理解其中的关键词语,恰当选用不等号,常用的表示不等关系的词语及对应的不等号如下表:
归纳总结
填一填
1.用不等号连接:
(1)2 -1;
(2)2+a -1+a;
(3)如x>0,则 2x -x;
(4)如y<0,则 2y -y;
(5) 2(m2+1) -(m2+1);
>
>
>
<
>
根据下列数量关系列不等式:
⑴a不是正数。
⑵x与y的一半的差大于-3。
⑶y的70%与5的和是非负数。
⑷3与x的倒数的差小于5。
⑸a的立方根不等于a。
上述不等式中那些是一元一次不等式( )。
⑴、 ⑶
例1:解下列不等式(组)并在数轴上表示出来。
(1) -
-5
解:去分母得:4(2x-1)-2(10x+1)
15x-60
移项,合并同类项 得:-27x
-54
x
2
在数轴上表示如图所示:
1
2
0
总结:
(1)去分母时,不等式中不含分母的项不要漏乘公分母
(2)去分母后,不等式中分子是多项式的要加括号
(3)最后一步将系数化为1时,要注意是否变向
二、一元一次不等式的解法
1.(1)若 的解集为 ,求a的取值范围________。
(2)若不等式(a-2)x>a-2的解集为x<1,求a的取值范围( )。
A .a < -2 B. a < 2 C. a >-2 D. a >2
(3)已知不等式(m-1)x>3的解集为x<-1,求m的值。
a<0
B
m=-2
4.由不等式(m-5)x>m-5变形为x<1,则m需满足的条件是 。
3.若a>b,且a、b为有理数,则am2 bm2。
6.若不等式组 无解,则a的取值范围是 ;
x> a+2
x<3a-2
2.若y= -x+7,且2≤y≤7,则x的取值范围是 ,
5.已知不等式3x-m ≤0有4个正整数解,则m的取值范围是 。
0≤x≤5
≥
m<5
12≤m≤15
a≤2
7.若 是关于x的一元一次不等式则 a 的值( )。
-2
1.若a>b ,则下列不等式中一定正确的是( )。
A.a–b<0
B.-5a < –5 b
C.a+8 <b+8
——
a
4
b
——
4
<
D.
B
练一练
2.已知关于x的不等式2x+m>-5的解集如图所示,则m的值为( )。
A.1 B.0
C.-1 D.-2
A
同大取大
的解集是
当a>b时,
X>a
X>b
X>a
同小取小
的解集是
当a>b时,
X<a
X<b
X<b
大小小大中间夹
的解集是
当a>b时,
X<a
X≥b
b≤X<a
大大小小定无解
的解集是
当a>b时,
X>a
X<b
无解
文字记忆
数学语言
图形
一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
b
三、一元一次不等式组的解法
解:由(1)得:2x+6>X+5,则x>-1,
由(2)得x-2
0则x
2,
原不等式组的解为:-12
用数轴表示:
2
0
-1
例2:解不等式组
2(x+3)>x+5 (1)
0 (2)
1.解集在数轴上表示为如图所示
的不等式组的是( )。
A. B.
C. D.
练一练
D
的解为 。
2.不等式组
-2试一试
1.关于 的不等式 的解集如图所示,
则a的值是 。
-2 -1 0 1 2
1
2.若不等式组 无解,
则a的取值范围是 。
x> a+2
x<3a-2
a≤2
解:由(1)得:2x+6>X+5,则x>-1;
由(2)得x-2
0则x
2
-12
用数轴表示:
2
0
-1
例3:解不等式组
2(x+3)>x+5 (1)
0 (2)
(1)解一元一次不等式组 2x+3≥4 ①
3x-2≤2x+3 ②
(2)不等式组4≤3x-2≤2x+3的所有整数解的和是 。
(3)如果4,3m-2,2m+3这三个数在数轴上所对应的点从左到右依次排列,则m的取值范围是 。
(4)不等式组 2x+3≥m 的解是 x≥5,则的取值范围
3x-2≥2x+3
是 。
14
2<m<5
m≤13
例4:
解这个不等式,得
∴y的正整数解是:1,2,3,4。
例5:y取何正整数时,代数式2(y-1)的值不大于10-4(y-3)的值。
解:根据题意列出不等式:
解:解方程组得:
x=-m+7
y=2m-5
因为它的解是正数,所以:
-m+7>0
2m-5>0
所以
2.5例6:求使方程组:
x+y=m+2
4x+5y=6m+3
的解x,y都是正数的m的取值范围。
例:王海贷款5万元去做生意,贷款月利息10‰。他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱?(精确到100元)
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答:王海平均每个月至少要赚8900元钱。
根据题意得取x=8900
做一做:
1.一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小明答对了x道题,则得4x分,另有(25-x)道要扣分,而小明评为优秀,即小明的得分应大于或等于85分,
4x-(25-x)≥85
解得:x≥22
所以,小明到少答对了22道题,他可能答对22,23,24或25道题。
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
y1=y2时,150x=160x-160,解得x=16;
y1>y2时,150x>160x-160,解得x<16;
y116;
2.某单位计划在新年期间组织员工到某地旅游,参如旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一定旅行社支付的旅游费用较少?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1,选择乙旅行社时,所需的费用为y2,则:
所以,当人数为16人时,甲、乙两家旅行社的收费相同;当人数为17~25人时,选择甲旅行社费用较少;当人数为10~15人时,选择乙旅行社费用较少。
谢 谢
第四章 一元一次不等式(组)
复习课件
一、知识导图
不等号的两边都是整式,而且只有一个未知数,未知数的最高次数是一次。
数轴、定点、定方向
用不等号连接而成的数学式子叫做不等式
关键 词语 第一类 (明确表明数量的不等关系) 第二类 (明确表明数量的范围特征)
大于、 比..大 小于、 比..小 不大于 不超过 不高于 至多 不小于 不低于 不少于 至少 正数 负数 非正数 非负数
不等号 > < ≤ ≥ >0 <0 ≤0 ≥0
用不等式表示不相等的数量关系(即列不等式)时,要正确理解其中的关键词语,恰当选用不等号,常用的表示不等关系的词语及对应的不等号如下表:
归纳总结
填一填
1.用不等号连接:
(1)2 -1;
(2)2+a -1+a;
(3)如x>0,则 2x -x;
(4)如y<0,则 2y -y;
(5) 2(m2+1) -(m2+1);
>
>
>
<
>
根据下列数量关系列不等式:
⑴a不是正数。
⑵x与y的一半的差大于-3。
⑶y的70%与5的和是非负数。
⑷3与x的倒数的差小于5。
⑸a的立方根不等于a。
上述不等式中那些是一元一次不等式( )。
⑴、 ⑶
例1:解下列不等式(组)并在数轴上表示出来。
(1) -
-5
解:去分母得:4(2x-1)-2(10x+1)
15x-60
移项,合并同类项 得:-27x
-54
x
2
在数轴上表示如图所示:
1
2
0
总结:
(1)去分母时,不等式中不含分母的项不要漏乘公分母
(2)去分母后,不等式中分子是多项式的要加括号
(3)最后一步将系数化为1时,要注意是否变向
二、一元一次不等式的解法
1.(1)若 的解集为 ,求a的取值范围________。
(2)若不等式(a-2)x>a-2的解集为x<1,求a的取值范围( )。
A .a < -2 B. a < 2 C. a >-2 D. a >2
(3)已知不等式(m-1)x>3的解集为x<-1,求m的值。
a<0
B
m=-2
4.由不等式(m-5)x>m-5变形为x<1,则m需满足的条件是 。
3.若a>b,且a、b为有理数,则am2 bm2。
6.若不等式组 无解,则a的取值范围是 ;
x> a+2
x<3a-2
2.若y= -x+7,且2≤y≤7,则x的取值范围是 ,
5.已知不等式3x-m ≤0有4个正整数解,则m的取值范围是 。
0≤x≤5
≥
m<5
12≤m≤15
a≤2
7.若 是关于x的一元一次不等式则 a 的值( )。
-2
1.若a>b ,则下列不等式中一定正确的是( )。
A.a–b<0
B.-5a < –5 b
C.a+8 <b+8
——
a
4
b
——
4
<
D.
B
练一练
2.已知关于x的不等式2x+m>-5的解集如图所示,则m的值为( )。
A.1 B.0
C.-1 D.-2
A
同大取大
的解集是
当a>b时,
X>a
X>b
X>a
同小取小
的解集是
当a>b时,
X<a
X<b
X<b
大小小大中间夹
的解集是
当a>b时,
X<a
X≥b
b≤X<a
大大小小定无解
的解集是
当a>b时,
X>a
X<b
无解
文字记忆
数学语言
图形
一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
b
三、一元一次不等式组的解法
解:由(1)得:2x+6>X+5,则x>-1,
由(2)得x-2
0则x
2,
原不等式组的解为:-1
用数轴表示:
2
0
-1
例2:解不等式组
2(x+3)>x+5 (1)
0 (2)
1.解集在数轴上表示为如图所示
的不等式组的是( )。
A. B.
C. D.
练一练
D
的解为 。
2.不等式组
-2
1.关于 的不等式 的解集如图所示,
则a的值是 。
-2 -1 0 1 2
1
2.若不等式组 无解,
则a的取值范围是 。
x> a+2
x<3a-2
a≤2
解:由(1)得:2x+6>X+5,则x>-1;
由(2)得x-2
0则x
2
-1
用数轴表示:
2
0
-1
例3:解不等式组
2(x+3)>x+5 (1)
0 (2)
(1)解一元一次不等式组 2x+3≥4 ①
3x-2≤2x+3 ②
(2)不等式组4≤3x-2≤2x+3的所有整数解的和是 。
(3)如果4,3m-2,2m+3这三个数在数轴上所对应的点从左到右依次排列,则m的取值范围是 。
(4)不等式组 2x+3≥m 的解是 x≥5,则的取值范围
3x-2≥2x+3
是 。
14
2<m<5
m≤13
例4:
解这个不等式,得
∴y的正整数解是:1,2,3,4。
例5:y取何正整数时,代数式2(y-1)的值不大于10-4(y-3)的值。
解:根据题意列出不等式:
解:解方程组得:
x=-m+7
y=2m-5
因为它的解是正数,所以:
-m+7>0
2m-5>0
所以
2.5
x+y=m+2
4x+5y=6m+3
的解x,y都是正数的m的取值范围。
例:王海贷款5万元去做生意,贷款月利息10‰。他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱?(精确到100元)
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答:王海平均每个月至少要赚8900元钱。
根据题意得取x=8900
做一做:
1.一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小明答对了x道题,则得4x分,另有(25-x)道要扣分,而小明评为优秀,即小明的得分应大于或等于85分,
4x-(25-x)≥85
解得:x≥22
所以,小明到少答对了22道题,他可能答对22,23,24或25道题。
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
y1=y2时,150x=160x-160,解得x=16;
y1>y2时,150x>160x-160,解得x<16;
y1
2.某单位计划在新年期间组织员工到某地旅游,参如旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一定旅行社支付的旅游费用较少?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1,选择乙旅行社时,所需的费用为y2,则:
所以,当人数为16人时,甲、乙两家旅行社的收费相同;当人数为17~25人时,选择甲旅行社费用较少;当人数为10~15人时,选择乙旅行社费用较少。
谢 谢
同课章节目录
