13.3.3 等边三角形的性质与判定 精品课件(共34张PPT)
文档属性
| 名称 | 13.3.3 等边三角形的性质与判定 精品课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 13:53:21 | ||
图片预览





文档简介
(共34张PPT)
八上数学同步精品课件
人教版八年级上册
13.3.3等边三角形的性质与判定
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.知道等边三角形的定义,等边三角形与等腰三角形的关系.
2.掌握等边三角形的性质和判定方法. (重点)
3.熟练地运用等边三角形的性质和判定方法解决问题. (难点)
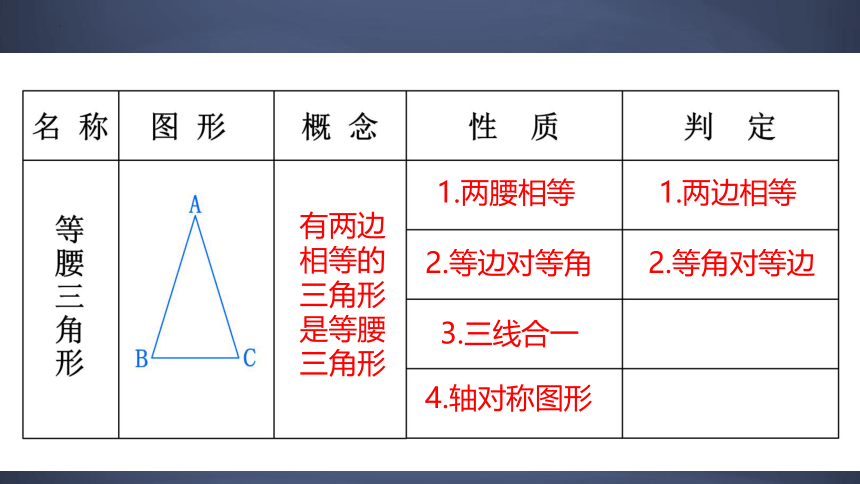
有两边相等的三角形是等腰三角形
1.两腰相等
2.等边对等角
3.三线合一
4.轴对称图形
1.两边相等
2.等角对等边
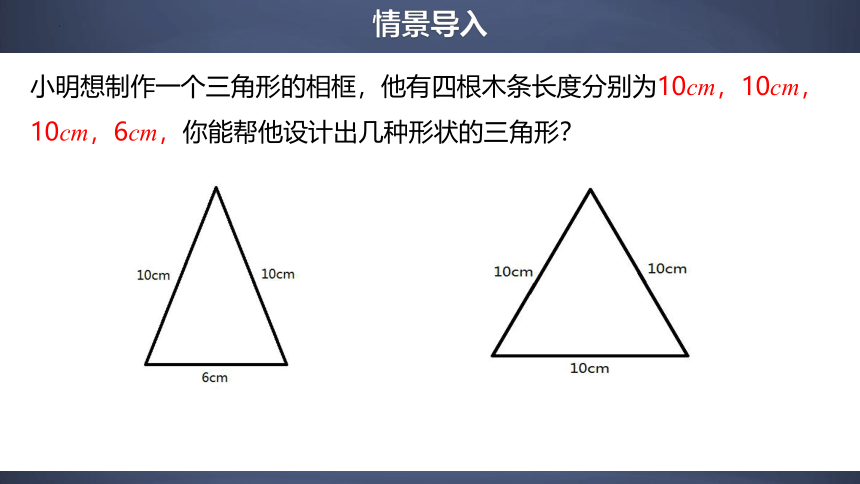
小明想制作一个三角形的相框,他有四根木条长度分别为10cm,10cm,10cm,6cm,你能帮他设计出几种形状的三角形?
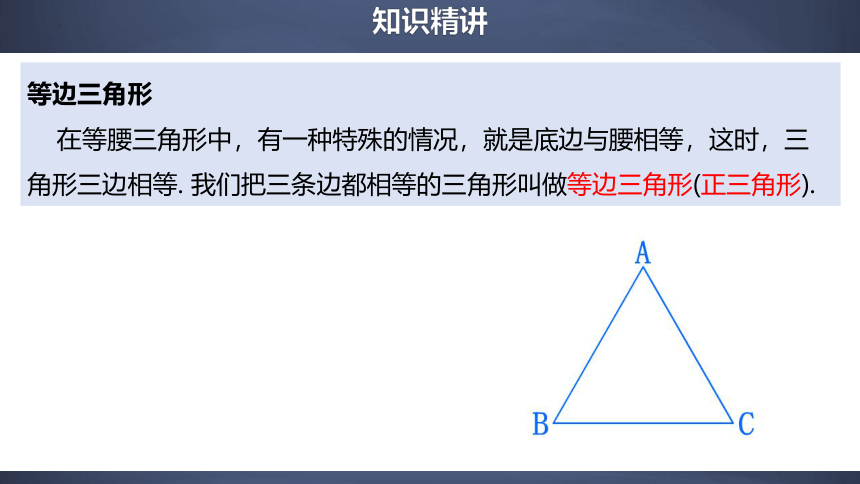
等边三角形
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等. 我们把三条边都相等的三角形叫做等边三角形(正三角形).
把等腰三角形的性质用于等边三角形,能得到什么结论?一个三角形的三个内角满足什么条件才是等边三角形?
1.等边三角形的三个内角都相等吗?为什么?
已知:如图,AB=AC=BC.
∵ AB=AC
∴ ∠B=∠C
同理 ∠A=∠C
∴ ∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°
性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
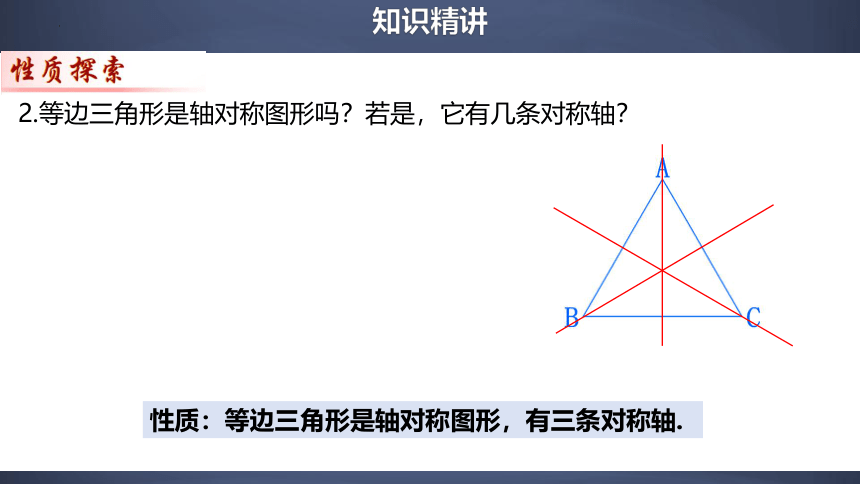
2.等边三角形是轴对称图形吗?若是,它有几条对称轴?
性质:等边三角形是轴对称图形,有三条对称轴.
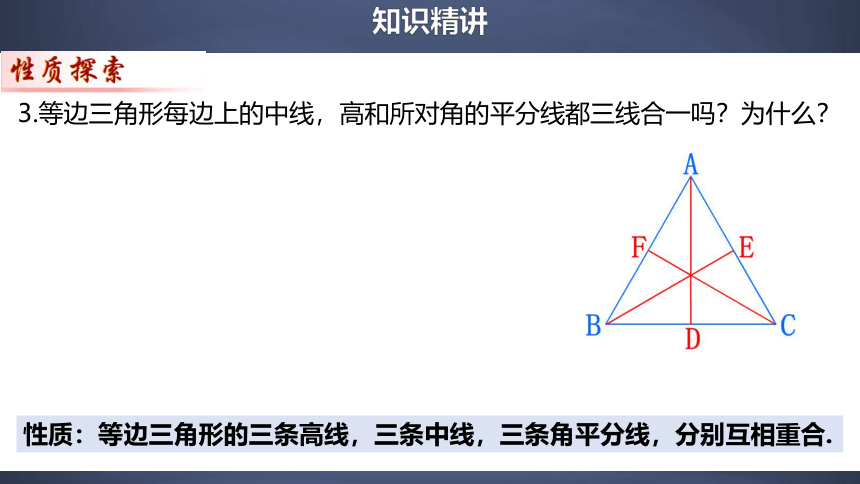
3.等边三角形每边上的中线,高和所对角的平分线都三线合一吗?为什么?
性质:等边三角形的三条高线,三条中线,三条角平分线,分别互相重合.
等边三角形的性质:
1.等边三角形的三边相等.
2.等边三角形的三个内角都相等,并每一个角都等于60°.
3.等边三角形的三条高线,三条中线,三条角平分线,分别互相重合.
4.等边三角形是轴对称图形,有三条对称轴.
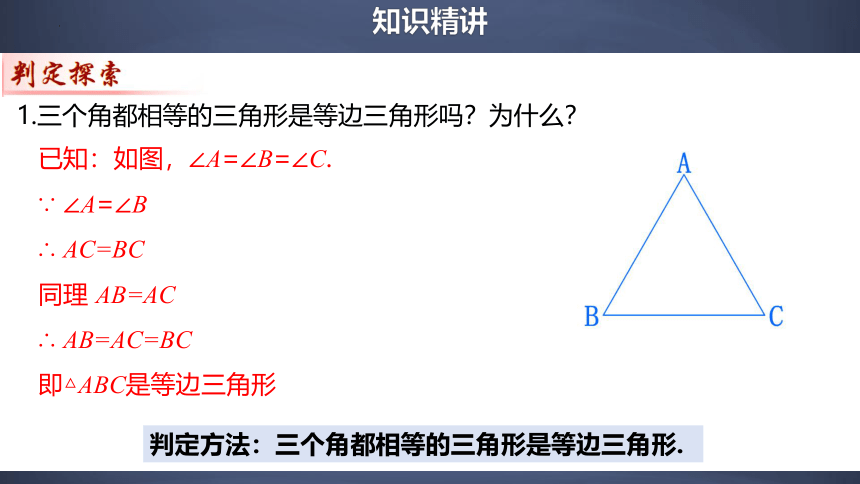
1.三个角都相等的三角形是等边三角形吗?为什么?
已知:如图,∠A=∠B=∠C.
∵ ∠A=∠B
∴ AC=BC
同理 AB=AC
∴ AB=AC=BC
即△ABC是等边三角形
判定方法:三个角都相等的三角形是等边三角形.
2.有一个角等于60°的等腰三角形是等边三角形. 你能证明这个结论吗?
假若AB=AC,则∠B=∠C
当顶角∠A=60°时,
∠B=∠C=(180°-60°)÷2=60°
∴ ∠A=∠B=∠C=60°
∴ △ABC是等边三角形.
当底角∠B=60°时,∠C=60°
∠A=180°-∠B-∠C=60°
∴ ∠A=∠B=∠C=60°
∴ △ABC是等边三角形.
判定方法:有一个角是60°的等腰三角形是等边三角形.
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
例1.如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵ △ABC是等边三角形
∴ ∠A=∠B=∠C
∵ DE∥BC
∴ ∠ADE=∠B,∠AED=∠C
∴ ∠A=∠ADE=∠AED
∴ △ADE是等边三角形
例1.如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵ △ABC是等边三角形
∴ ∠A=∠B=∠C=60°
∵ DE∥BC
∴ ∠ADE=∠B,∠AED=∠C
∴ ∠ADE=∠AED
∴ AD=AE,且∠A=60°
∴ △ADE是等边三角形
例2.如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
【点睛】等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合“等边对等角”、三角形的内角和与外角的性质.
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
例3.△ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BNC(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN=∠ABC=60°.
【点睛】此题属于等边三角形与全等三角形的综合运用,一般是利用等边三角形的性质判定三角形全等,而后利用全等及等边三角形的性质,求角度或证明边相等.
例4.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=60°
∴△APQ是等边三角形.
【点睛】判定一个三角形是等边三角形有以下方法:一是证明三角形三条边相等;二是证明三角形三个内角相等;三是先证明三角形是等腰三角形,再证明有一个内角等于60°.
如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
例5.图①、图②中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1)如图①,线段AN与线段BM是否相等?请说明理由;
(2)如图②,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.
解:(1)AN=BM.
理由:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°.
∴∠ACN=∠MCB.
∴△ACN≌△MCB(SAS).
∴AN=BM.
(1)如图①,线段AN与线段BM是否相等?请说明理由;
(2)△CEF是等边三角形.
证明:∵∠ACE=∠FCM=60°,
∴∠ECF=60°.
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
∵AC=MC,
∴△ACE≌△MCF(ASA),
∴CE=CF. ∴△CEF是等边三角形.
(2)如图②,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
2.如图,△ABC为等边三角形,AD⊥BC,AE=AD则∠ADE的度数为( )
A.30° B.60° C.45 D.75°
D
D
3.下列推理中,错误的是( )
A.因为∠A=∠B=∠C,所以△ABC是等边三角形
B.因为AB=AC且∠B=∠C,所以△ABC是等边三角形
C.因为∠A=60°,∠B=60°,所以△ABC是等边三角形
D.因为AB=AC,∠B=60°,所以△ABC是等边三角形
B
4.已知AD是等边△ABC的高,且BD=1cm,那么BC的长是_____cm.
5.若等边△ABC的两条角平分线BD与CE交于点O,则∠BOC的度数为_____.
6.如图,△ABC是周长为6的等边三角形,BD为中线,且BD=a,E为BC延长线上一点,CE=CD,则△BDE的周长为________.
2
120°
2a+3
7.如图,等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′ ,EB′分别交AC于点F,G,若∠ADF=80°,则∠EGC的度数为______.
80°
8.如图,△ABC和△BDE都是等边三角形,且点E在BC上.求证:AE=CD.
证明:△ABC和△BDE都是等边三角形.
∴AB=BC,BE=BD
∠ABC=∠EBD=60°
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS)
∴AE=CD
9.如图,△ABC是等边三角形,∠ABC、∠ACB的平分线交于点O,OM∥AB,ON∥AC.求证:BM=MN=CN.
证明:∵△ABC是等边三角形
∴∠ABC=60°
又∵OB平分∠ABC
∴∠1=∠2=30°
又∵OM//AB
∴∠1=∠3
∴∠2=∠3=30°
∴BM=OM,∠OMN=60°
同理CN=ON,∠ONM=60°
∴∠OMN=∠ONM=∠MON=60°
∴OM=ON=MN ∴BM=MN=CN
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
13.3.3等边三角形的性质与判定
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.知道等边三角形的定义,等边三角形与等腰三角形的关系.
2.掌握等边三角形的性质和判定方法. (重点)
3.熟练地运用等边三角形的性质和判定方法解决问题. (难点)
有两边相等的三角形是等腰三角形
1.两腰相等
2.等边对等角
3.三线合一
4.轴对称图形
1.两边相等
2.等角对等边
小明想制作一个三角形的相框,他有四根木条长度分别为10cm,10cm,10cm,6cm,你能帮他设计出几种形状的三角形?
等边三角形
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等. 我们把三条边都相等的三角形叫做等边三角形(正三角形).
把等腰三角形的性质用于等边三角形,能得到什么结论?一个三角形的三个内角满足什么条件才是等边三角形?
1.等边三角形的三个内角都相等吗?为什么?
已知:如图,AB=AC=BC.
∵ AB=AC
∴ ∠B=∠C
同理 ∠A=∠C
∴ ∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°
性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
2.等边三角形是轴对称图形吗?若是,它有几条对称轴?
性质:等边三角形是轴对称图形,有三条对称轴.
3.等边三角形每边上的中线,高和所对角的平分线都三线合一吗?为什么?
性质:等边三角形的三条高线,三条中线,三条角平分线,分别互相重合.
等边三角形的性质:
1.等边三角形的三边相等.
2.等边三角形的三个内角都相等,并每一个角都等于60°.
3.等边三角形的三条高线,三条中线,三条角平分线,分别互相重合.
4.等边三角形是轴对称图形,有三条对称轴.
1.三个角都相等的三角形是等边三角形吗?为什么?
已知:如图,∠A=∠B=∠C.
∵ ∠A=∠B
∴ AC=BC
同理 AB=AC
∴ AB=AC=BC
即△ABC是等边三角形
判定方法:三个角都相等的三角形是等边三角形.
2.有一个角等于60°的等腰三角形是等边三角形. 你能证明这个结论吗?
假若AB=AC,则∠B=∠C
当顶角∠A=60°时,
∠B=∠C=(180°-60°)÷2=60°
∴ ∠A=∠B=∠C=60°
∴ △ABC是等边三角形.
当底角∠B=60°时,∠C=60°
∠A=180°-∠B-∠C=60°
∴ ∠A=∠B=∠C=60°
∴ △ABC是等边三角形.
判定方法:有一个角是60°的等腰三角形是等边三角形.
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
例1.如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵ △ABC是等边三角形
∴ ∠A=∠B=∠C
∵ DE∥BC
∴ ∠ADE=∠B,∠AED=∠C
∴ ∠A=∠ADE=∠AED
∴ △ADE是等边三角形
例1.如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵ △ABC是等边三角形
∴ ∠A=∠B=∠C=60°
∵ DE∥BC
∴ ∠ADE=∠B,∠AED=∠C
∴ ∠ADE=∠AED
∴ AD=AE,且∠A=60°
∴ △ADE是等边三角形
例2.如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
【点睛】等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合“等边对等角”、三角形的内角和与外角的性质.
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
例3.△ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BNC(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN=∠ABC=60°.
【点睛】此题属于等边三角形与全等三角形的综合运用,一般是利用等边三角形的性质判定三角形全等,而后利用全等及等边三角形的性质,求角度或证明边相等.
例4.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=60°
∴△APQ是等边三角形.
【点睛】判定一个三角形是等边三角形有以下方法:一是证明三角形三条边相等;二是证明三角形三个内角相等;三是先证明三角形是等腰三角形,再证明有一个内角等于60°.
如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
例5.图①、图②中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1)如图①,线段AN与线段BM是否相等?请说明理由;
(2)如图②,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.
解:(1)AN=BM.
理由:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°.
∴∠ACN=∠MCB.
∴△ACN≌△MCB(SAS).
∴AN=BM.
(1)如图①,线段AN与线段BM是否相等?请说明理由;
(2)△CEF是等边三角形.
证明:∵∠ACE=∠FCM=60°,
∴∠ECF=60°.
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
∵AC=MC,
∴△ACE≌△MCF(ASA),
∴CE=CF. ∴△CEF是等边三角形.
(2)如图②,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
2.如图,△ABC为等边三角形,AD⊥BC,AE=AD则∠ADE的度数为( )
A.30° B.60° C.45 D.75°
D
D
3.下列推理中,错误的是( )
A.因为∠A=∠B=∠C,所以△ABC是等边三角形
B.因为AB=AC且∠B=∠C,所以△ABC是等边三角形
C.因为∠A=60°,∠B=60°,所以△ABC是等边三角形
D.因为AB=AC,∠B=60°,所以△ABC是等边三角形
B
4.已知AD是等边△ABC的高,且BD=1cm,那么BC的长是_____cm.
5.若等边△ABC的两条角平分线BD与CE交于点O,则∠BOC的度数为_____.
6.如图,△ABC是周长为6的等边三角形,BD为中线,且BD=a,E为BC延长线上一点,CE=CD,则△BDE的周长为________.
2
120°
2a+3
7.如图,等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′ ,EB′分别交AC于点F,G,若∠ADF=80°,则∠EGC的度数为______.
80°
8.如图,△ABC和△BDE都是等边三角形,且点E在BC上.求证:AE=CD.
证明:△ABC和△BDE都是等边三角形.
∴AB=BC,BE=BD
∠ABC=∠EBD=60°
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS)
∴AE=CD
9.如图,△ABC是等边三角形,∠ABC、∠ACB的平分线交于点O,OM∥AB,ON∥AC.求证:BM=MN=CN.
证明:∵△ABC是等边三角形
∴∠ABC=60°
又∵OB平分∠ABC
∴∠1=∠2=30°
又∵OM//AB
∴∠1=∠3
∴∠2=∠3=30°
∴BM=OM,∠OMN=60°
同理CN=ON,∠ONM=60°
∴∠OMN=∠ONM=∠MON=60°
∴OM=ON=MN ∴BM=MN=CN
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
