13.3.4 含30°角的直角三角形的性质 精品课件(共33张PPT)
文档属性
| 名称 | 13.3.4 含30°角的直角三角形的性质 精品课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 17:45:28 | ||
图片预览






文档简介
(共33张PPT)
八上数学同步精品课件
人教版八年级上册
13.3.4 含30°角的直角三角形的性质
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.探索含30°角的直角三角形的性质.(重点)
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.(难点)
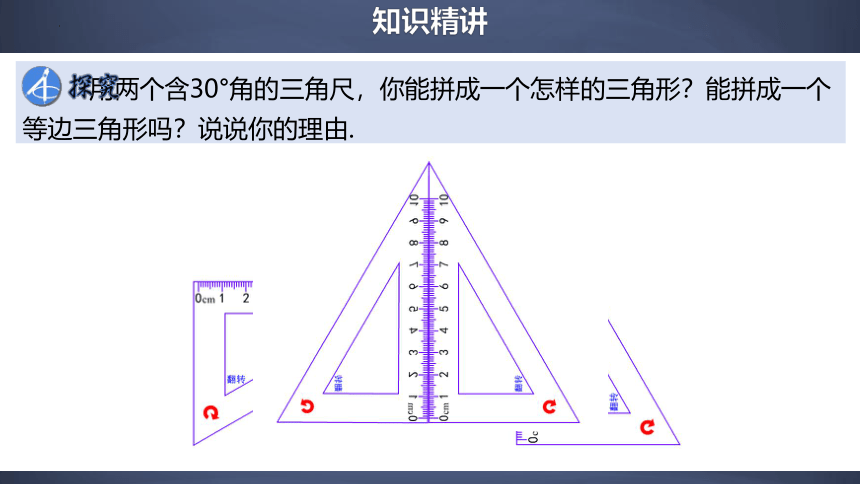
用两个含30°角的三角尺,你能拼成一个怎样的三角形?能拼成一个等边三角形吗?说说你的理由.
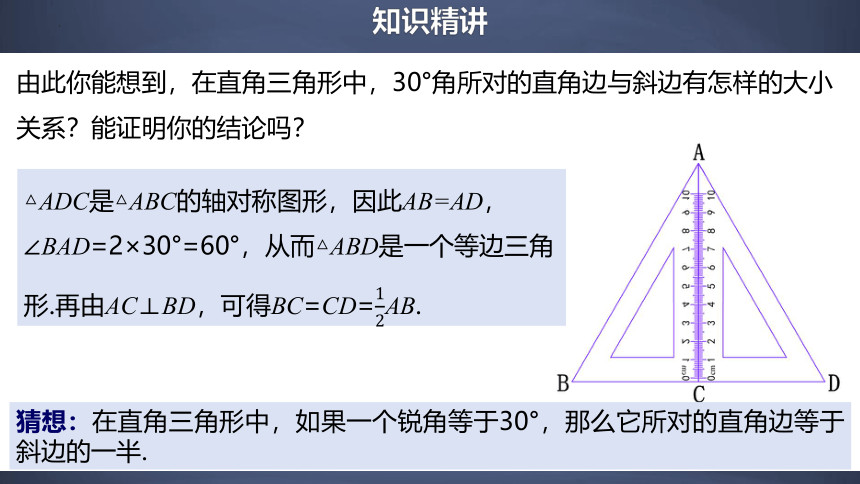
由此你能想到,在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?能证明你的结论吗?
△ADC是△ABC的轴对称图形,因此AB=AD,∠BAD=2×30°=60°,从而△ABD是一个等边三角形.再由AC⊥BD,可得BC=CD=AB.
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°. 求证:BC=AB.
证法①倍长法
证明:延长BC到D,使BD=AB,连接AD.
∵ ∠ACB=90°,∠BAC=30°
∴ ∠B=60°
∴ △ABD是等边三角形
∵ AC⊥BD
∴ BC=BD
∴ BC=AB
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°. 求证:BC=AB.
证法②截半法
证明:在BA上截取BD=BC,连接DC.
∵ ∠B=90°-∠A=60°,BD=BC
∴ △BCD是等边三角形
∴ ∠BDC=60°,BD=DC=BC
∴ ∠DCA=∠BDC-∠A=30°=∠A
∴ AD=DC=BD=BC
∴ AB=AD+BD=2BC
∴ BC=AB
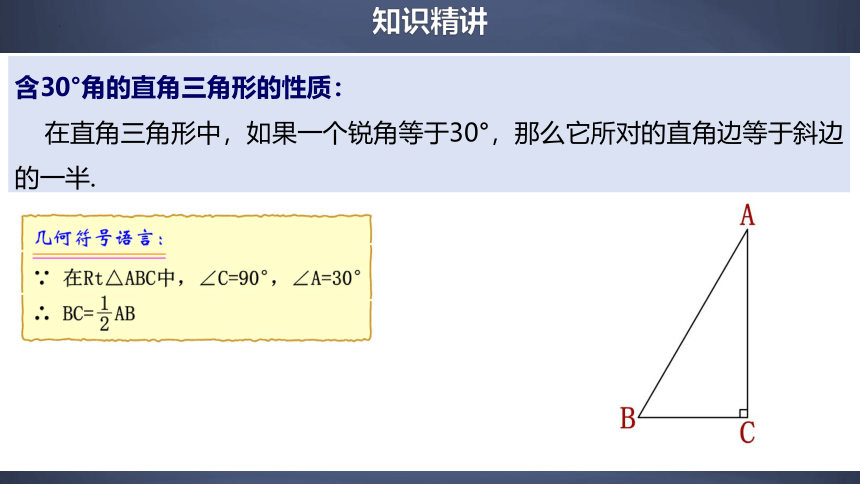
含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
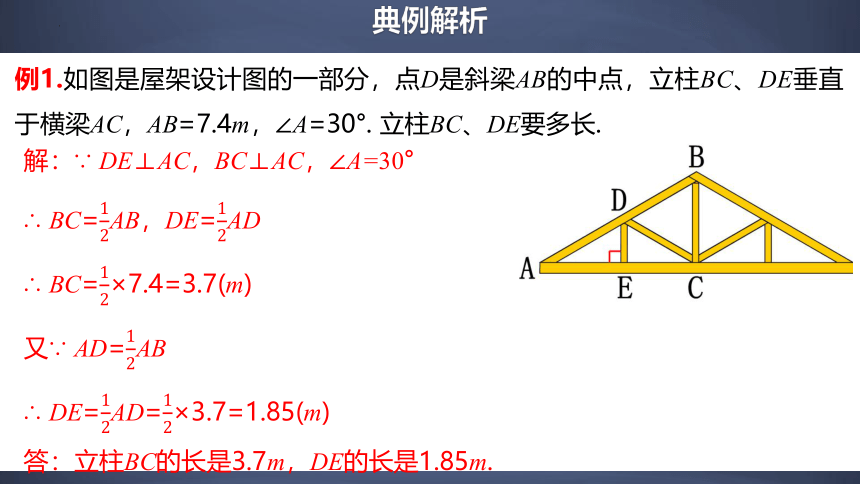
例1.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°. 立柱BC、DE要多长.
解:∵ DE⊥AC,BC⊥AC,∠A=30°
∴ BC=AB,DE=AD
∴ BC=×7.4=3.7(m)
又∵ AD=AB
∴ DE=AD=×3.7=1.85(m)
答:立柱BC的长是3.7m,DE的长是1.85m.
如图1所示的是某超市人口的双翼闸门,当它的双翼展开时,如图2,双翼边缘的端点A与B之间的距离为12cm,双翼的边缘AC=BD=62cm,且与闸机侧立面夹角∠ACP=∠BDQ=30°.求当双翼收起时,可以通过闸机的物体的最大宽度.
解:如图,过点A作AE⊥CP于点E,过点B作BF⊥DQ于点F,
在Rt△ACE中,∠ACE=30°,
∴AE=AC=×62=31(cm),
同理可得,BF=31cm,
又∵双翼边缘的端点A与B之间的距离为12cm,
∴31+12+31=74(cm),
∴当双翼收起时,可以通过闸机的物体的最大宽度为74cm.
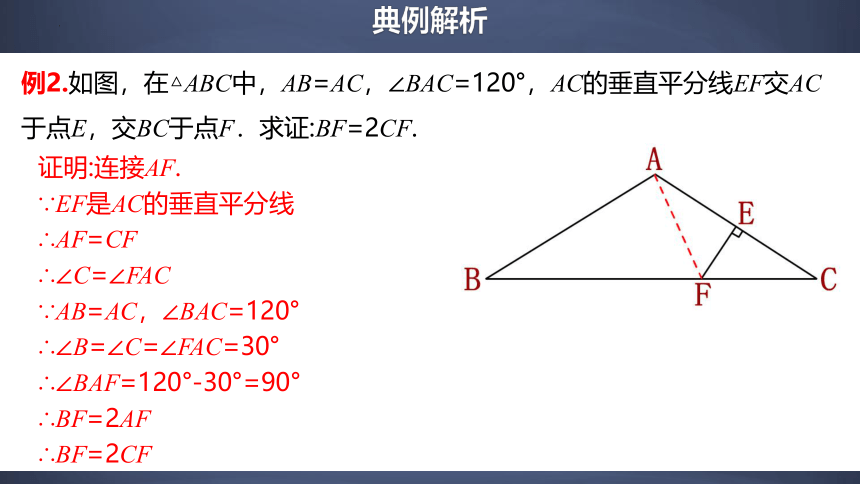
例2.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
证明:连接AF.
∵EF是AC的垂直平分线
∴AF=CF
∴∠C=∠FAC
∵AB=AC,∠BAC=120°
∴∠B=∠C=∠FAC=30°
∴∠BAF=120°-30°=90°
∴BF=2AF
∴BF=2CF
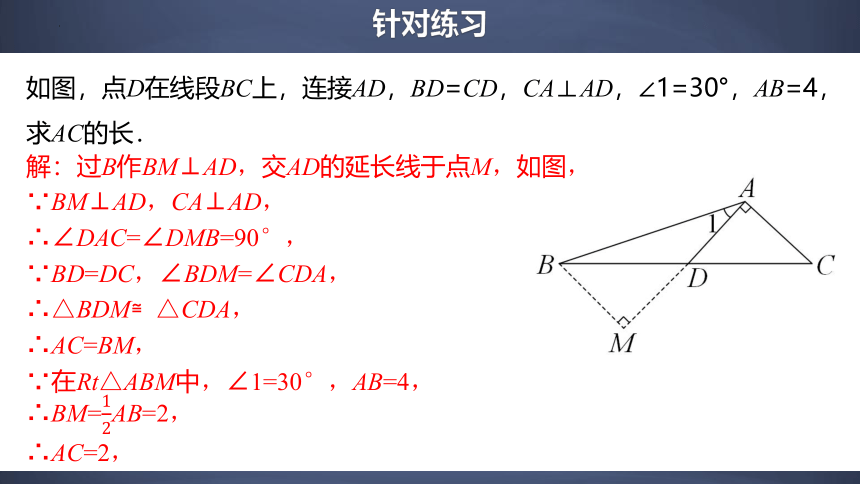
如图,点D在线段BC上,连接AD,BD=CD,CA⊥AD,∠1=30°,AB=4,求AC的长.
解:过B作BM⊥AD,交AD的延长线于点M,如图,
∵BM⊥AD,CA⊥AD,
∴∠DAC=∠DMB=90°,
∵BD=DC,∠BDM=∠CDA,
∴△BDM≌△CDA,
∴AC=BM,
∵在Rt△ABM中,∠1=30°,AB=4,
∴BM=AB=2,
∴AC=2,
例3.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)当AD取何值时,DE=EF
解:(1)△ABC为等边三角形
∴AB=AC=BC=8,∠B=∠C=60°
∵AD=2 ∴BD=AB-AD=6
在Rt△BDE中,∠BDE=90°-∠B=30°
∴BE=BD=3
∴CE=BC-BE=5
在Rt△CFE中,∠CEF=90°-∠C=30°
∴CF=CE=
∴AF=AC-FC=
解:(2)在△BDE和△CEF中,
∴△BDE≌△CEF(AAS)
∴BE=CF
∵∠CEF=30°∴BE=CF=EC
∴BE=BC= ∴BD=2BE=
例3.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)当AD取何值时,DE=EF
∴AD=AB-BD=8-=
∴当AD=时,DE=EF
如图,Rt△ACB中,∠ACB=90°,∠A=30°,∠ABC的平分线BE交AC于点E.点D为AB上一点,且AD=AC,CD、BE交于点M.(1)求∠DMB的度数;
(1)解:∵∠ACB=90°,∠A=30°
∴∠ABC=60°
∴BE是∠ABC的平分线
∴∠ABE=∠CBE=30°
∵∠A=30°,AC=AD
∴∠ACD=∠ADC=75°
∴∠DMB=∠ADC-∠ABE=45°
(2)证明:∵∠ACB=90°,∠A=30°
∴AB=2BC
∵CH⊥BE,∠CBE=30°
∴BC=2CH ∴AB=4CH
∵∠CMH=∠DMB=45°
∴∠CMH=∠MCH=45°
∴CH=MH
∴AB=4MH
如图,Rt△ACB中,∠ACB=90°,∠A=30°,∠ABC的平分线BE交AC于点E.点D为AB上一点,且AD=AC,CD、BE交于点M.
(2)若CH⊥BE于点H,求证:AB=4MH.
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(1)求证:BE=AD;
(2)求∠BMN的度数;
(3)若MN=3cm,ME=1cm,则AD= cm.
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(1)求证:BE=AD;
(1)证明:∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=.
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS),
∴BE=AD;
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(2)求∠BMN的度数;
(2)解:由(1)得:△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BAD+∠CAD=,
∴∠BAD+∠ABE=.
∴∠BMN=∠ABE+∠BAD=;
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(3)若MN=3cm,ME=1cm,则AD= cm.
(3)解:∵△ABE≌△CAD,
∴BE=AD,
∵BN⊥AD,
∴∠BNM=,
∴∠MBN=﹣∠BMN=,
∵MN=3cm,ME=1cm,
∴BM=2MN=6(cm),
∴AD=BE=BM+ME=6+1=7(cm).
1.如图(1),△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
D
2.如图(2),是某商场一楼与二楼之间的手扶电梯示意图.其中AB,CD分别表示一楼,二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.3m B.4m C.5m D.6m
B
3.如图,在Rt△ABC中,∠C=90°,DE垂直平分AB,垂足为D,交BC于E,AE平分∠BAC,那么下列关系式中不成立的是( )
A.∠B=∠CAE B.∠DEA=∠CEA C.AB=2AC D.AC=2EC
D
4.已知一个三角形的三个内角的比是1:2:3,最短边为5cm,则最长边为
_____cm.
5.如图,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于E,若AD=3cm,则AB=____cm,BE=_____cm.
10
6
4.5
6.如图(3),∠BAC=30°,AM是∠BAC的平分线,过点M作ME∥BA交AC于点E,作MD⊥BA,垂足为D,ME=10cm,则MD=_____cm.
7.将一副三角尺按如图(4)所示方式叠放在一起,若AB=16cm,则阴影部分的面积是_____cm2.
5
32
8.Rt△ABC中,∠C=90°,∠B=2∠A,∠B和∠A各是多少度?边AB与BC之间有什么关系?
解:如图,∵ ∠C=90°
∴ ∠A+∠B=90°
又∵ ∠B=2∠A
∴ 3∠A=90°
∴ ∠A=30°,∠B=60°
∴ BC=AB或AB=2BC
9.如图,在Rt△ABC中,∠C=90°, ∠BAC=60°,∠BAC的平分线AM长为15cm,求BC的长.
解:在Rt△ABC中,∠C=90°, ∠BAC=60°
∴∠B=30°
∵AM平分∠BAC
∴∠CAM=∠BAM=30°
∴∠B=∠BAM
∴AM=BM=15cm
在Rt△ACM中,∠C=90°,∠CAM=30°
∴CM=AM=7.5cm
∴BC=CM+BM=7.5+15=22.5(cm)
10.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB.DE恰好是∠ADB的平分线.CD与DB有怎样的数量关系?请说明理由.
解:
理由如下:∵DE⊥AB,
∴∠AED=∠BED=90°.
∵DE是∠ADB的平分线,
∴∠ADE=∠BDE.
又∵DE=DE,
∴△AED≌△BED(ASA),
在Rt△ACD中,∵∠CAD=30°,
∴AD=BD,∠DAE=∠B.
∵∠BAD=∠CAD= ∠BAC,
∴∠BAD=∠CAD=∠B.
∵∠BAD+∠CAD+∠B=90°,
∴∠B=∠BAD=∠CAD=30°.
∴CD= AD= BD,即CD= DB.
含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
13.3.4 含30°角的直角三角形的性质
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.探索含30°角的直角三角形的性质.(重点)
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.(难点)
用两个含30°角的三角尺,你能拼成一个怎样的三角形?能拼成一个等边三角形吗?说说你的理由.
由此你能想到,在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?能证明你的结论吗?
△ADC是△ABC的轴对称图形,因此AB=AD,∠BAD=2×30°=60°,从而△ABD是一个等边三角形.再由AC⊥BD,可得BC=CD=AB.
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°. 求证:BC=AB.
证法①倍长法
证明:延长BC到D,使BD=AB,连接AD.
∵ ∠ACB=90°,∠BAC=30°
∴ ∠B=60°
∴ △ABD是等边三角形
∵ AC⊥BD
∴ BC=BD
∴ BC=AB
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°. 求证:BC=AB.
证法②截半法
证明:在BA上截取BD=BC,连接DC.
∵ ∠B=90°-∠A=60°,BD=BC
∴ △BCD是等边三角形
∴ ∠BDC=60°,BD=DC=BC
∴ ∠DCA=∠BDC-∠A=30°=∠A
∴ AD=DC=BD=BC
∴ AB=AD+BD=2BC
∴ BC=AB
含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
例1.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°. 立柱BC、DE要多长.
解:∵ DE⊥AC,BC⊥AC,∠A=30°
∴ BC=AB,DE=AD
∴ BC=×7.4=3.7(m)
又∵ AD=AB
∴ DE=AD=×3.7=1.85(m)
答:立柱BC的长是3.7m,DE的长是1.85m.
如图1所示的是某超市人口的双翼闸门,当它的双翼展开时,如图2,双翼边缘的端点A与B之间的距离为12cm,双翼的边缘AC=BD=62cm,且与闸机侧立面夹角∠ACP=∠BDQ=30°.求当双翼收起时,可以通过闸机的物体的最大宽度.
解:如图,过点A作AE⊥CP于点E,过点B作BF⊥DQ于点F,
在Rt△ACE中,∠ACE=30°,
∴AE=AC=×62=31(cm),
同理可得,BF=31cm,
又∵双翼边缘的端点A与B之间的距离为12cm,
∴31+12+31=74(cm),
∴当双翼收起时,可以通过闸机的物体的最大宽度为74cm.
例2.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
证明:连接AF.
∵EF是AC的垂直平分线
∴AF=CF
∴∠C=∠FAC
∵AB=AC,∠BAC=120°
∴∠B=∠C=∠FAC=30°
∴∠BAF=120°-30°=90°
∴BF=2AF
∴BF=2CF
如图,点D在线段BC上,连接AD,BD=CD,CA⊥AD,∠1=30°,AB=4,求AC的长.
解:过B作BM⊥AD,交AD的延长线于点M,如图,
∵BM⊥AD,CA⊥AD,
∴∠DAC=∠DMB=90°,
∵BD=DC,∠BDM=∠CDA,
∴△BDM≌△CDA,
∴AC=BM,
∵在Rt△ABM中,∠1=30°,AB=4,
∴BM=AB=2,
∴AC=2,
例3.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)当AD取何值时,DE=EF
解:(1)△ABC为等边三角形
∴AB=AC=BC=8,∠B=∠C=60°
∵AD=2 ∴BD=AB-AD=6
在Rt△BDE中,∠BDE=90°-∠B=30°
∴BE=BD=3
∴CE=BC-BE=5
在Rt△CFE中,∠CEF=90°-∠C=30°
∴CF=CE=
∴AF=AC-FC=
解:(2)在△BDE和△CEF中,
∴△BDE≌△CEF(AAS)
∴BE=CF
∵∠CEF=30°∴BE=CF=EC
∴BE=BC= ∴BD=2BE=
例3.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)当AD取何值时,DE=EF
∴AD=AB-BD=8-=
∴当AD=时,DE=EF
如图,Rt△ACB中,∠ACB=90°,∠A=30°,∠ABC的平分线BE交AC于点E.点D为AB上一点,且AD=AC,CD、BE交于点M.(1)求∠DMB的度数;
(1)解:∵∠ACB=90°,∠A=30°
∴∠ABC=60°
∴BE是∠ABC的平分线
∴∠ABE=∠CBE=30°
∵∠A=30°,AC=AD
∴∠ACD=∠ADC=75°
∴∠DMB=∠ADC-∠ABE=45°
(2)证明:∵∠ACB=90°,∠A=30°
∴AB=2BC
∵CH⊥BE,∠CBE=30°
∴BC=2CH ∴AB=4CH
∵∠CMH=∠DMB=45°
∴∠CMH=∠MCH=45°
∴CH=MH
∴AB=4MH
如图,Rt△ACB中,∠ACB=90°,∠A=30°,∠ABC的平分线BE交AC于点E.点D为AB上一点,且AD=AC,CD、BE交于点M.
(2)若CH⊥BE于点H,求证:AB=4MH.
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(1)求证:BE=AD;
(2)求∠BMN的度数;
(3)若MN=3cm,ME=1cm,则AD= cm.
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(1)求证:BE=AD;
(1)证明:∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=.
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS),
∴BE=AD;
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(2)求∠BMN的度数;
(2)解:由(1)得:△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BAD+∠CAD=,
∴∠BAD+∠ABE=.
∴∠BMN=∠ABE+∠BAD=;
例4.已知,如图,△ABC为等边三角形,点E在AC边上,点D在BC边上,并且AE=CD,AD和BE相交于点M,BN⊥AD于N.
(3)若MN=3cm,ME=1cm,则AD= cm.
(3)解:∵△ABE≌△CAD,
∴BE=AD,
∵BN⊥AD,
∴∠BNM=,
∴∠MBN=﹣∠BMN=,
∵MN=3cm,ME=1cm,
∴BM=2MN=6(cm),
∴AD=BE=BM+ME=6+1=7(cm).
1.如图(1),△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
D
2.如图(2),是某商场一楼与二楼之间的手扶电梯示意图.其中AB,CD分别表示一楼,二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.3m B.4m C.5m D.6m
B
3.如图,在Rt△ABC中,∠C=90°,DE垂直平分AB,垂足为D,交BC于E,AE平分∠BAC,那么下列关系式中不成立的是( )
A.∠B=∠CAE B.∠DEA=∠CEA C.AB=2AC D.AC=2EC
D
4.已知一个三角形的三个内角的比是1:2:3,最短边为5cm,则最长边为
_____cm.
5.如图,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于E,若AD=3cm,则AB=____cm,BE=_____cm.
10
6
4.5
6.如图(3),∠BAC=30°,AM是∠BAC的平分线,过点M作ME∥BA交AC于点E,作MD⊥BA,垂足为D,ME=10cm,则MD=_____cm.
7.将一副三角尺按如图(4)所示方式叠放在一起,若AB=16cm,则阴影部分的面积是_____cm2.
5
32
8.Rt△ABC中,∠C=90°,∠B=2∠A,∠B和∠A各是多少度?边AB与BC之间有什么关系?
解:如图,∵ ∠C=90°
∴ ∠A+∠B=90°
又∵ ∠B=2∠A
∴ 3∠A=90°
∴ ∠A=30°,∠B=60°
∴ BC=AB或AB=2BC
9.如图,在Rt△ABC中,∠C=90°, ∠BAC=60°,∠BAC的平分线AM长为15cm,求BC的长.
解:在Rt△ABC中,∠C=90°, ∠BAC=60°
∴∠B=30°
∵AM平分∠BAC
∴∠CAM=∠BAM=30°
∴∠B=∠BAM
∴AM=BM=15cm
在Rt△ACM中,∠C=90°,∠CAM=30°
∴CM=AM=7.5cm
∴BC=CM+BM=7.5+15=22.5(cm)
10.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB.DE恰好是∠ADB的平分线.CD与DB有怎样的数量关系?请说明理由.
解:
理由如下:∵DE⊥AB,
∴∠AED=∠BED=90°.
∵DE是∠ADB的平分线,
∴∠ADE=∠BDE.
又∵DE=DE,
∴△AED≌△BED(ASA),
在Rt△ACD中,∵∠CAD=30°,
∴AD=BD,∠DAE=∠B.
∵∠BAD=∠CAD= ∠BAC,
∴∠BAD=∠CAD=∠B.
∵∠BAD+∠CAD+∠B=90°,
∴∠B=∠BAD=∠CAD=30°.
∴CD= AD= BD,即CD= DB.
含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
