空间向量与立体几何 核心素养练--2022-2023学年高二数学人教A版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 空间向量与立体几何 核心素养练--2022-2023学年高二数学人教A版(2019)选择性必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 17:01:03 | ||
图片预览



文档简介
空间向量与立体几何核心素养练
左图是常见的一种灭火器消防箱,抽象成数学模型如右图所示的六面体,其中四边形和为直角梯形,、、、为直角顶点,其他四个面均为矩形,,,,下列说法正确的是( )
A. 该几何体是四棱台
B. 该几何体是棱柱,面是底面
C.
D. 面与面所成锐二面角为
我国古代数学名著九章算术商功中记载“斜解立方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.在堑堵中,,为的中点,则( )
A. B. C. D.
如图,在长方体中,,,点、分别为和上的动点,若平面,则的最小值为( )
A. B. C. D.
九章算术中将底面为直角三角形且侧棱垂直于底面的三棱柱称为堑堵.在堑堵中,若,,点为线段的中点,则点到平面的距离为( )
A. B. C. D.
在我国古代数学名著九章算术中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑中,平面,,且,为的中点,则二面角的正弦值为( )
A. B. C. D.
假设地球是半径为的球体,现将空间直角坐标系的原点置于球心,赤道位于平面上,轴的正方向为球心指向正北极方向,本初子午线弧是度经线,位于平面上,且交轴于点,如图所示,已知赤道上一点位于东经度,则地球上位于东经度、北纬度的空间点的坐标为( )
A. B.
C. D.
如图,正方体的棱长为,分别是棱的中点,下列结论正确的有( )
A. 面
B. 过三点所得正方体的截面的面积为
C. 直线与平面所成的线面角的正弦值为
D. 三棱锥的外接球的直径为
年美国数学学会出了一道题:一个正四面体和一个正四棱锥的所有棱长都相等,将正四面体的一个面和正四棱锥的一个侧面紧贴重合在一起,得到一个新几何体.中学生丹尼尔做了一个如图所示的模型寄给美国数学学会,美国数学学会根据丹尼尔的模型修改了有关结论.对于该新几何体,则( )
A. B.
C. 新几何体有个面 D. 新几何体的六个顶点在同一个球面上
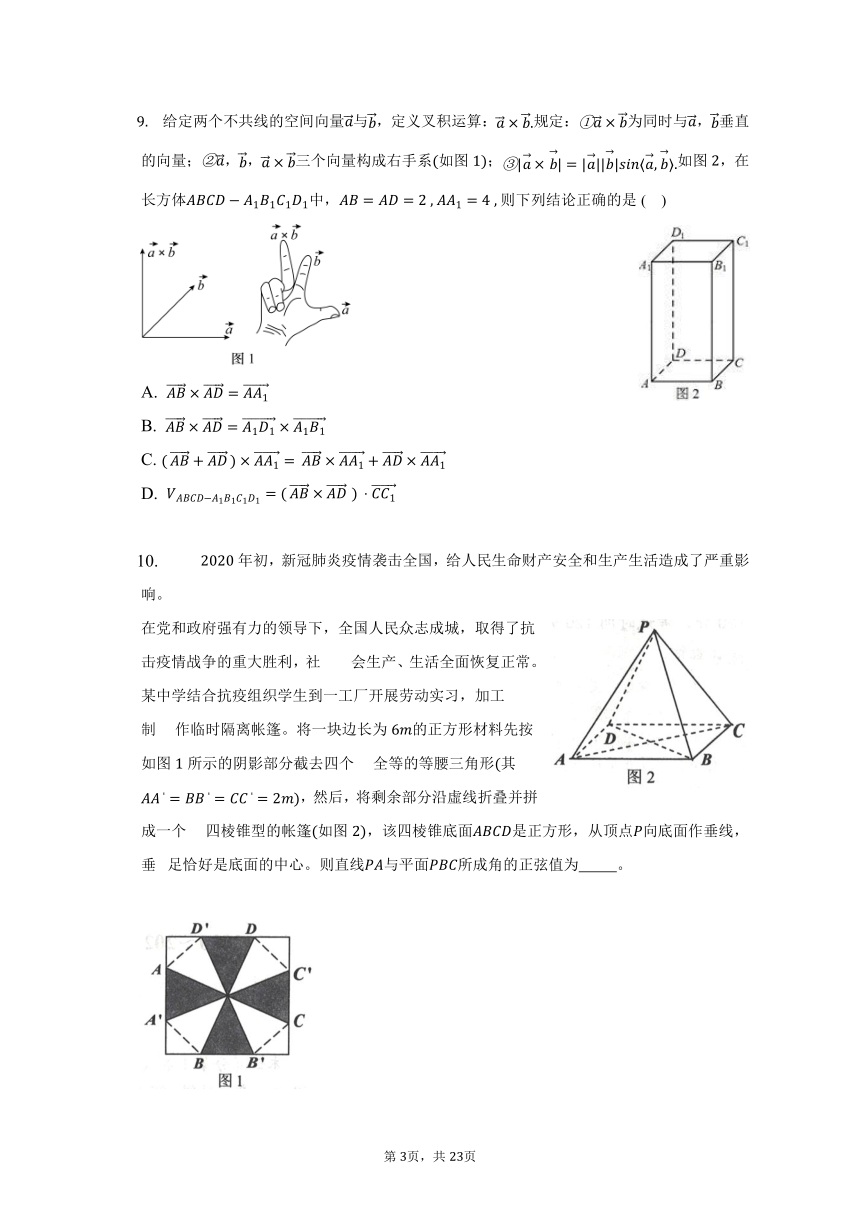
给定两个不共线的空间向量与,定义叉积运算:规定:为同时与,垂直的向量;,,三个向量构成右手系如图;如图,在长方体中,则下列结论正确的是( )
A.
B.
C.
D.
年初,新冠肺炎疫情袭击全国,给人民生命财产安全和生产生活造成了严重影响。
在党和政府强有力的领导下,全国人民众志成城,取得了抗击疫情战争的重大胜利,社 会生产、生活全面恢复正常。某中学结合抗疫组织学生到一工厂开展劳动实习,加工制 作临时隔离帐篷。将一块边长为的正方形材料先按如图所示的阴影部分截去四个 全等的等腰三角形其,然后,将剩余部分沿虛线折叠并拼成一个 四棱锥型的帐篷如图,该四棱锥底面是正方形,从顶点向底面作垂线,垂 足恰好是底面的中心。则直线与平面所成角的正弦值为 。
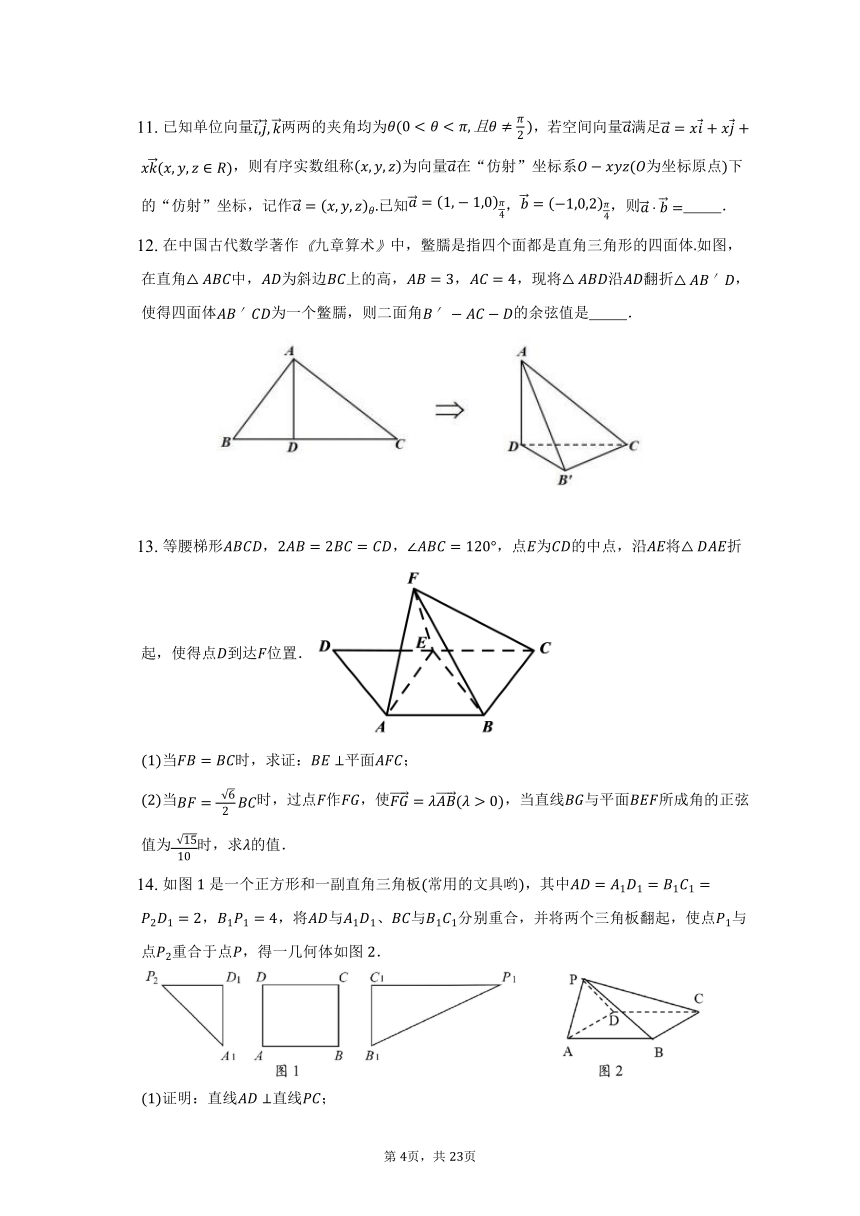
已知单位向量两两的夹角均为,若空间向量满足,则有序实数组称为向量在“仿射”坐标系为坐标原点下的“仿射”坐标,记作已知,,则 .
在中国古代数学著作九章算术中,鳖臑是指四个面都是直角三角形的四面体如图,在直角中,为斜边上的高,,,现将沿翻折,使得四面体为一个鳖臑,则二面角的余弦值是 .
等腰梯形,,,点为的中点,沿将折起,使得点到达位置.
当时,求证:平面;
当时,过点作,使,当直线与平面所成角的正弦值为时,求的值.
如图是一个正方形和一副直角三角板常用的文具哟,其中,,将与、与分别重合,并将两个三角板翻起,使点与点重合于点,得一几何体如图.
证明:直线直线;
求平面与平面的夹角的正弦值;
在正方形面范围内有以圆心为、半径为的一段圆弧,则在该段圆弧上,是否存在点使得异面直线与所成的角是,试说明你的理由.
九章算术是我国古代的数学著作,是“算经十书”中最重要的一部,它对几何学的研究比西方要早多年在九章算术中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵如图,在堑堵中,,,,分别是,的中点,点在线段上
若为的中点,求证:平面.
是否存在点,使得平面与平面所成的二面角为?若存在,试确定点的位置;若不存在,请说明理由.
在,,平面平面这三个条件中任选一个,补充在下面问题的横线上,并解答.问题:已知在三棱锥中,为的中点,__________,.
证明:;
若,,为线段上一点,且,求二面角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
答案和解析
1.【答案】
【解析】
【分析】
本题考查棱柱、棱台的概念、利用空间向量判定线线垂直、利用空间向量求二面角,属于中档题.
根据棱柱、棱台的概念直接判定、选项;建立空间直角坐标系,求出的坐标,利用即可判定选项;分别求出面与面的一个法向量,设面与面所成锐二面角为 ,由即可判定选项.
【解答】
解:由四棱台和棱柱的概念可知,,B错误;
根据题意,以为坐标原点,,,所在的直线分别为,,轴,建立如图所示空间直角坐标系,
则,
所以,
则,
所以与不垂直,故C错误;
因为平面,
所以平面的一个法向量为,
设平面的一个法向量为,
且,
由得,解得,
令,得,
所以,
设面与面所成锐二面角为 ,
则,
所以面与面所成锐二面角为,故D正确.
故选D.
2.【答案】
【解析】
【分析】
本题考查了空间向量基本定理及线性运算,向量数量积的运算,属于中档题.
由条件得,,,将,用向量,,表示,代入数量积的公式进行运算可得结果.
【解答】
解:根据堑堵的几何性质可知,,,,
因为,,
所以
故选A.
3.【答案】
【解析】
【分析】
本题考查求空间线段的长度的最小值,考查推理能力和计算能力,属于较难题.
方法:建立如图空间直角坐标系,设,,,根据已知求出,的关系,从而把建立关于的二次函数,通过二次函数求最值.
方法:作于点,作于点,则设出各边长度根据勾股定理和二次函数即能求出的最小值.
【解答】
方法一:解:如图建系,由题意可设,,
,,,,
又,,
设平面的法向量,
则,令,
平面的法向量,
又面,即,
,最小值为.
故选A.
方法二:
解:如图,作于点,作于点,则,
则可得,平面,所以、、、四点共面,
因为线段平面,平面,且,
所以平面平面,
由面面平行的性质定理得.
所以四边形为直角梯形,
设,则,,,
在直角梯形中,
,
当时,的最小值为.
故选:.
4.【答案】
【解析】
【分析】
本题主要考查空间中点到平面的距离,属于中档题.
根据题意建立空间直角坐标系,求出平面的法向量,再利用空间中点到平面的距离公式得出结论.
【解答】
解:如图,在堑堵中,由可知,.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,,,,
,,,.
设平面的法向量为: ,
则
取,得:,
设点到平面的距离为,
则,
故答案选:.
5.【答案】
【解析】
【分析】
本题考查二面角的正弦值求法,属于中档题.
取的中点,连接,则平面,作,为垂足,连接,
则,所以是二面角的平面角不妨设,即可求出二面角的正弦值.
【解答】
解:取的中点,连接,
则平面,
作,为垂足,连接,可知平面,
则,所以是二面角的平面角.
不妨设,根据题意可知
,,
,
故选C.
6.【答案】
【解析】
【分析】
本题主要考查立体几何中的空间点的位置,考查了学生的空间想象能力,属于中档题.
根据图形求出点在平面上的投影的坐标,进而求出点的坐标即可.
【解答】
解:设点投影到平面上的点,则又与轴正向的夹角为,
由在轴与轴的投影可知因此点的坐标为
故选:.
7.【答案】
【解析】
【分析】
本题考查了线面平行的判定,三棱锥的外接球,直线与平面所成的角,对知识迁移能力要求较高,属于难题.
根据线面平行的判定可得A正确,计算截面的面积可得B错误,利用空间向量求得直线与平面所成的线面角的正弦值可得C正确,求得三棱锥的外接球的直径可得D错误.
【解答】
解:对于,如下图,过三点所得正方体的截面为六边形,且各个顶点分别在所在棱的中点处,
六边形为正六边形,且边长为,面积,B错误;
对于,,平面,平面,面,A正确;
以为坐标原点,、、所在的直线分别为轴、轴、轴建立如图所示的空间直角坐标系,
则,,,则
设平面的法向量为,则,即
令,解得,,
可得,又,
设直线与平面所成的线面角为,则,故C正确;
对于,正方体平面,平面,,
又,,平面,平面,平面,,,,
同理可证,,,平面,
平面,由正方体的对称性可得到平面的距离为,
又,在平面上的射影正好处于的中心,记为点,此时,如图所示,
设三棱锥外接球球心为,则,
设,则,得,
外接球半径,直径为,D错误.
故选AC.
8.【答案】
【解析】
【分析】
本题考查简单几何体的平行与垂直,利用空间向量求两点间的距离,属于中档题.
设正四面体和正四棱锥的所有棱长都为,如图建立空间直角坐标系,由距离公式求得的长度,利用余弦定理求出,从而得出,,,四点共面,可判断;由可判断;由三棱柱有个面可判断;由三棱柱为斜三棱柱判定.
【解答】
解:设正四面体和正四棱锥的所有棱长都为,如图建立空间直角坐标系,
则,,,
,
设,由,得
解得:
,,
,.
,
,,,四点共面,
四边形为平行四边形,,A正确;
,,B正确;
新几何体为一个三棱柱共个面,C错误;
此三棱柱为斜三棱柱,故不可能有外接球,故D错误.
故选AB.
9.【答案】
【解析】
【分析】
本题主要考查空间向量的新定义运算,属于中档题.
利用空间向量的新定义运算,对每个选项逐项进行判断,即可得结论.
【解答】
解:对于选项A:同时与,垂直,
,
,
又因为,
所以,
故成立,故A正确.
对于选项B:因为,,三个向量构成右手系,
所以,,
,故B错误.
对于选项C:对于,
同时满足垂直于,且满足右手系,
所以,,,
,解得,
所以;
对于,
,,,
,,
,,
,,
,,
所以,
综合可得,故C正确.
对于选项D:长方体的体积,
,
所以长方体的体积,故D正确.
故选ACD.
10.【答案】
【解析】
【分析】
本题考查利用空间向量求直线和平面所成角,中档题.
根据题意以为原点,,,分别为,,轴建立空间直角坐标系,求出向量,平面的一个法向量,利用夹角公式求出即可.
【解答】
解:设,交于,根据题意以为原点,,,分别为,,轴建立空间直角坐标系,
由题意知,所以,正方形的边长为,
则,,,,
,
设平面的一个法向量为,,,
由
令,,,,
设直线与平面所成的角为,
,
故答案为:.
11.【答案】
【解析】
【分析】
本题考查对新定义的理解,还考查向量数量积的坐标表示,属于拔高题.
根据新定义结合向量数量积的坐标表示,可得结果.
【解答】
解:
则
由
,
则
故答案为:
12.【答案】
【解析】
【分析】
本题考查利用空间向量求二面角的余弦值,属于中档题.
根据题意,在长宽高分别为,,的长方体中作出四面体,并以为坐标原点,为轴,为轴,建立空间直角坐标系,然后求出平面的一个法向量,平面的一个法向量,根据二面角的余弦值公式,即可求出答案,注意二面角是锐角,所以二面角的余弦值应为正值.
【解答】
解:在直角中,为斜边上的高,,,
则,,,,
即在四面体中,,,,,,则,
要使四面体为鳖臑,根据三角形中大边对大角,
可知需要平面,此时,,,为直角,
满足四面体为一个鳖臑,则,
如下图在长宽高分别为,,的长方体中作出四面体,
如上图,以为坐标原点建立空间直角坐标系,
则,,,,
,,,,
设向量为平面的法向量,向量为平面的法向量,
则
可取,同理可取,
,,
又因二面角锐角,
所以二面角的余弦值是.
故答案为.
13.【答案】解:由折叠前的图形可知:,为等边三角形,四边形为菱形
连接,交于点,连接,则
当时,为等边三角形;
;
又面,面,,
平面
取中点为,连接,;
,
设,,
,又
以为坐标原点,建立如图所示坐标系;
则,
因为,可得:
,
设是平面的一个法向量,
则
令,得
设直线与平面所成角,则,
即,
解得:或,又,故.
【解析】本题主要考查了线面垂直的判定以及向量法求直线与平面所成角,属于较难题.
利用线面垂直的判定定理求证即可;
建立空间直角坐标系,求出平面的一个法向量,利用线面角公式求得的值.
14.【答案】(1)证明:由题意可知,AD⊥PD,AD⊥DC,且PD∩DC=D,PD,DC平面PDC,
∴AD⊥平面PDC,又PC平面PDC,∴AD⊥PC;
(2)由(1)知,AD⊥平面PCD,以点D为原点O建立空间直角坐标系,如图:
P在平面yDz内,在中,,利用余弦定理可得,所以可以得到P到y轴距离为,到z轴距离为1,所以P(0,-1,),
D(0,0,0),A(2,0,0),B(2,2,0),
所以,
易知是平面PCD的一个法向量,
设平面PAB的一个法向量为,
则,取z=2,则x=,y=0,所以,
则.
记两个平面的夹角为,则;
(3)存在,如上图可知,C(0,2,0),所以,
因为点Q在平面xDy内,可设Q(m,s,0),则,
由题意可知,,
所以,
又Q在平面xDy平面内,以点D为圆心,半径为2的一段圆弧的方程为,点Q在圆弧上,
所以有,
解得,
所以点Q的坐标为,故存在符合题意的点Q.
【解析】本题考查空间位置关系的证明,考查空间向量的应用,属于较难题.
(1)利用线面垂直的判定定理得到AD⊥平面PDC,即可证明;
(2)建立空间直角坐标系,利用空间向量求出二面角的大小的正弦值;
(3)设Q(m,s,0),利用空间向量的夹角公式得到,又Q在平面xOy平面内,以点D为圆心,半径为2的一段圆弧上,得到方程组求解即可判断是否存在.
15.【答案】解:证明:取的中点,连接,
因为为的中点, 且,
又为的中点,为的中点,所以 且,
故A 且,
所以四边形为平行四边形,
所以 ,
又平面,平面,
所以 平面;
以为原点,,,所在直线分别为轴轴轴,建立空间直角坐标系,
则,,,
易知平面的一个法向量为.
假设满足条件的点存在,令,
则,.
设平面的一个法向量是,
则,即
令,得,,所以
由题意得,,
解得,
故点不在线段上
【解析】本题考查线面平行的判定,考查利用空间向量求二面角的余弦值,考查推理论证能力、运算求解能力、空间想象能力,属于中档题.
根据题意结合三角形的中位线,平行四边形以及线面平行的判定定理即可求解;
以为原点,为轴,为轴,为轴建立空间直角坐标系,设,利用向量法表示出平面与平面所成的二面角为时的余弦值,解方程即可求解.
16.【答案】解:证明:若选,则,,,,
,且,平面,平面,平面,
若选,则,,,≌,,,
,,,且,平面,平面,平面,
若选,则,,,平面平面,平面平面,平面,
平面,平面,.
,, ,,平面,平面
又,,,两两垂直,如图,以为原点,
分别以,,的方向为,,轴的正方向,建立空间直角坐标系,
则,,,,
由于,可知,
,,
设为平面的法向量,
则即 取,则,,故可取,
易知为平面的一个法向量.
,
设二面角的平面角为,由图可得为锐角,
.
【解析】本题考查线线垂直,空间向量求二面角,属于中档题.
选条件证明平面,即可证明;
建立空间直角坐标系,求平面的一个法向量,为平面的一个法向量,利用空间向量法求解即可.
第1页,共1页
左图是常见的一种灭火器消防箱,抽象成数学模型如右图所示的六面体,其中四边形和为直角梯形,、、、为直角顶点,其他四个面均为矩形,,,,下列说法正确的是( )
A. 该几何体是四棱台
B. 该几何体是棱柱,面是底面
C.
D. 面与面所成锐二面角为
我国古代数学名著九章算术商功中记载“斜解立方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.在堑堵中,,为的中点,则( )
A. B. C. D.
如图,在长方体中,,,点、分别为和上的动点,若平面,则的最小值为( )
A. B. C. D.
九章算术中将底面为直角三角形且侧棱垂直于底面的三棱柱称为堑堵.在堑堵中,若,,点为线段的中点,则点到平面的距离为( )
A. B. C. D.
在我国古代数学名著九章算术中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑中,平面,,且,为的中点,则二面角的正弦值为( )
A. B. C. D.
假设地球是半径为的球体,现将空间直角坐标系的原点置于球心,赤道位于平面上,轴的正方向为球心指向正北极方向,本初子午线弧是度经线,位于平面上,且交轴于点,如图所示,已知赤道上一点位于东经度,则地球上位于东经度、北纬度的空间点的坐标为( )
A. B.
C. D.
如图,正方体的棱长为,分别是棱的中点,下列结论正确的有( )
A. 面
B. 过三点所得正方体的截面的面积为
C. 直线与平面所成的线面角的正弦值为
D. 三棱锥的外接球的直径为
年美国数学学会出了一道题:一个正四面体和一个正四棱锥的所有棱长都相等,将正四面体的一个面和正四棱锥的一个侧面紧贴重合在一起,得到一个新几何体.中学生丹尼尔做了一个如图所示的模型寄给美国数学学会,美国数学学会根据丹尼尔的模型修改了有关结论.对于该新几何体,则( )
A. B.
C. 新几何体有个面 D. 新几何体的六个顶点在同一个球面上
给定两个不共线的空间向量与,定义叉积运算:规定:为同时与,垂直的向量;,,三个向量构成右手系如图;如图,在长方体中,则下列结论正确的是( )
A.
B.
C.
D.
年初,新冠肺炎疫情袭击全国,给人民生命财产安全和生产生活造成了严重影响。
在党和政府强有力的领导下,全国人民众志成城,取得了抗击疫情战争的重大胜利,社 会生产、生活全面恢复正常。某中学结合抗疫组织学生到一工厂开展劳动实习,加工制 作临时隔离帐篷。将一块边长为的正方形材料先按如图所示的阴影部分截去四个 全等的等腰三角形其,然后,将剩余部分沿虛线折叠并拼成一个 四棱锥型的帐篷如图,该四棱锥底面是正方形,从顶点向底面作垂线,垂 足恰好是底面的中心。则直线与平面所成角的正弦值为 。
已知单位向量两两的夹角均为,若空间向量满足,则有序实数组称为向量在“仿射”坐标系为坐标原点下的“仿射”坐标,记作已知,,则 .
在中国古代数学著作九章算术中,鳖臑是指四个面都是直角三角形的四面体如图,在直角中,为斜边上的高,,,现将沿翻折,使得四面体为一个鳖臑,则二面角的余弦值是 .
等腰梯形,,,点为的中点,沿将折起,使得点到达位置.
当时,求证:平面;
当时,过点作,使,当直线与平面所成角的正弦值为时,求的值.
如图是一个正方形和一副直角三角板常用的文具哟,其中,,将与、与分别重合,并将两个三角板翻起,使点与点重合于点,得一几何体如图.
证明:直线直线;
求平面与平面的夹角的正弦值;
在正方形面范围内有以圆心为、半径为的一段圆弧,则在该段圆弧上,是否存在点使得异面直线与所成的角是,试说明你的理由.
九章算术是我国古代的数学著作,是“算经十书”中最重要的一部,它对几何学的研究比西方要早多年在九章算术中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵如图,在堑堵中,,,,分别是,的中点,点在线段上
若为的中点,求证:平面.
是否存在点,使得平面与平面所成的二面角为?若存在,试确定点的位置;若不存在,请说明理由.
在,,平面平面这三个条件中任选一个,补充在下面问题的横线上,并解答.问题:已知在三棱锥中,为的中点,__________,.
证明:;
若,,为线段上一点,且,求二面角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
答案和解析
1.【答案】
【解析】
【分析】
本题考查棱柱、棱台的概念、利用空间向量判定线线垂直、利用空间向量求二面角,属于中档题.
根据棱柱、棱台的概念直接判定、选项;建立空间直角坐标系,求出的坐标,利用即可判定选项;分别求出面与面的一个法向量,设面与面所成锐二面角为 ,由即可判定选项.
【解答】
解:由四棱台和棱柱的概念可知,,B错误;
根据题意,以为坐标原点,,,所在的直线分别为,,轴,建立如图所示空间直角坐标系,
则,
所以,
则,
所以与不垂直,故C错误;
因为平面,
所以平面的一个法向量为,
设平面的一个法向量为,
且,
由得,解得,
令,得,
所以,
设面与面所成锐二面角为 ,
则,
所以面与面所成锐二面角为,故D正确.
故选D.
2.【答案】
【解析】
【分析】
本题考查了空间向量基本定理及线性运算,向量数量积的运算,属于中档题.
由条件得,,,将,用向量,,表示,代入数量积的公式进行运算可得结果.
【解答】
解:根据堑堵的几何性质可知,,,,
因为,,
所以
故选A.
3.【答案】
【解析】
【分析】
本题考查求空间线段的长度的最小值,考查推理能力和计算能力,属于较难题.
方法:建立如图空间直角坐标系,设,,,根据已知求出,的关系,从而把建立关于的二次函数,通过二次函数求最值.
方法:作于点,作于点,则设出各边长度根据勾股定理和二次函数即能求出的最小值.
【解答】
方法一:解:如图建系,由题意可设,,
,,,,
又,,
设平面的法向量,
则,令,
平面的法向量,
又面,即,
,最小值为.
故选A.
方法二:
解:如图,作于点,作于点,则,
则可得,平面,所以、、、四点共面,
因为线段平面,平面,且,
所以平面平面,
由面面平行的性质定理得.
所以四边形为直角梯形,
设,则,,,
在直角梯形中,
,
当时,的最小值为.
故选:.
4.【答案】
【解析】
【分析】
本题主要考查空间中点到平面的距离,属于中档题.
根据题意建立空间直角坐标系,求出平面的法向量,再利用空间中点到平面的距离公式得出结论.
【解答】
解:如图,在堑堵中,由可知,.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,,,,
,,,.
设平面的法向量为: ,
则
取,得:,
设点到平面的距离为,
则,
故答案选:.
5.【答案】
【解析】
【分析】
本题考查二面角的正弦值求法,属于中档题.
取的中点,连接,则平面,作,为垂足,连接,
则,所以是二面角的平面角不妨设,即可求出二面角的正弦值.
【解答】
解:取的中点,连接,
则平面,
作,为垂足,连接,可知平面,
则,所以是二面角的平面角.
不妨设,根据题意可知
,,
,
故选C.
6.【答案】
【解析】
【分析】
本题主要考查立体几何中的空间点的位置,考查了学生的空间想象能力,属于中档题.
根据图形求出点在平面上的投影的坐标,进而求出点的坐标即可.
【解答】
解:设点投影到平面上的点,则又与轴正向的夹角为,
由在轴与轴的投影可知因此点的坐标为
故选:.
7.【答案】
【解析】
【分析】
本题考查了线面平行的判定,三棱锥的外接球,直线与平面所成的角,对知识迁移能力要求较高,属于难题.
根据线面平行的判定可得A正确,计算截面的面积可得B错误,利用空间向量求得直线与平面所成的线面角的正弦值可得C正确,求得三棱锥的外接球的直径可得D错误.
【解答】
解:对于,如下图,过三点所得正方体的截面为六边形,且各个顶点分别在所在棱的中点处,
六边形为正六边形,且边长为,面积,B错误;
对于,,平面,平面,面,A正确;
以为坐标原点,、、所在的直线分别为轴、轴、轴建立如图所示的空间直角坐标系,
则,,,则
设平面的法向量为,则,即
令,解得,,
可得,又,
设直线与平面所成的线面角为,则,故C正确;
对于,正方体平面,平面,,
又,,平面,平面,平面,,,,
同理可证,,,平面,
平面,由正方体的对称性可得到平面的距离为,
又,在平面上的射影正好处于的中心,记为点,此时,如图所示,
设三棱锥外接球球心为,则,
设,则,得,
外接球半径,直径为,D错误.
故选AC.
8.【答案】
【解析】
【分析】
本题考查简单几何体的平行与垂直,利用空间向量求两点间的距离,属于中档题.
设正四面体和正四棱锥的所有棱长都为,如图建立空间直角坐标系,由距离公式求得的长度,利用余弦定理求出,从而得出,,,四点共面,可判断;由可判断;由三棱柱有个面可判断;由三棱柱为斜三棱柱判定.
【解答】
解:设正四面体和正四棱锥的所有棱长都为,如图建立空间直角坐标系,
则,,,
,
设,由,得
解得:
,,
,.
,
,,,四点共面,
四边形为平行四边形,,A正确;
,,B正确;
新几何体为一个三棱柱共个面,C错误;
此三棱柱为斜三棱柱,故不可能有外接球,故D错误.
故选AB.
9.【答案】
【解析】
【分析】
本题主要考查空间向量的新定义运算,属于中档题.
利用空间向量的新定义运算,对每个选项逐项进行判断,即可得结论.
【解答】
解:对于选项A:同时与,垂直,
,
,
又因为,
所以,
故成立,故A正确.
对于选项B:因为,,三个向量构成右手系,
所以,,
,故B错误.
对于选项C:对于,
同时满足垂直于,且满足右手系,
所以,,,
,解得,
所以;
对于,
,,,
,,
,,
,,
,,
所以,
综合可得,故C正确.
对于选项D:长方体的体积,
,
所以长方体的体积,故D正确.
故选ACD.
10.【答案】
【解析】
【分析】
本题考查利用空间向量求直线和平面所成角,中档题.
根据题意以为原点,,,分别为,,轴建立空间直角坐标系,求出向量,平面的一个法向量,利用夹角公式求出即可.
【解答】
解:设,交于,根据题意以为原点,,,分别为,,轴建立空间直角坐标系,
由题意知,所以,正方形的边长为,
则,,,,
,
设平面的一个法向量为,,,
由
令,,,,
设直线与平面所成的角为,
,
故答案为:.
11.【答案】
【解析】
【分析】
本题考查对新定义的理解,还考查向量数量积的坐标表示,属于拔高题.
根据新定义结合向量数量积的坐标表示,可得结果.
【解答】
解:
则
由
,
则
故答案为:
12.【答案】
【解析】
【分析】
本题考查利用空间向量求二面角的余弦值,属于中档题.
根据题意,在长宽高分别为,,的长方体中作出四面体,并以为坐标原点,为轴,为轴,建立空间直角坐标系,然后求出平面的一个法向量,平面的一个法向量,根据二面角的余弦值公式,即可求出答案,注意二面角是锐角,所以二面角的余弦值应为正值.
【解答】
解:在直角中,为斜边上的高,,,
则,,,,
即在四面体中,,,,,,则,
要使四面体为鳖臑,根据三角形中大边对大角,
可知需要平面,此时,,,为直角,
满足四面体为一个鳖臑,则,
如下图在长宽高分别为,,的长方体中作出四面体,
如上图,以为坐标原点建立空间直角坐标系,
则,,,,
,,,,
设向量为平面的法向量,向量为平面的法向量,
则
可取,同理可取,
,,
又因二面角锐角,
所以二面角的余弦值是.
故答案为.
13.【答案】解:由折叠前的图形可知:,为等边三角形,四边形为菱形
连接,交于点,连接,则
当时,为等边三角形;
;
又面,面,,
平面
取中点为,连接,;
,
设,,
,又
以为坐标原点,建立如图所示坐标系;
则,
因为,可得:
,
设是平面的一个法向量,
则
令,得
设直线与平面所成角,则,
即,
解得:或,又,故.
【解析】本题主要考查了线面垂直的判定以及向量法求直线与平面所成角,属于较难题.
利用线面垂直的判定定理求证即可;
建立空间直角坐标系,求出平面的一个法向量,利用线面角公式求得的值.
14.【答案】(1)证明:由题意可知,AD⊥PD,AD⊥DC,且PD∩DC=D,PD,DC平面PDC,
∴AD⊥平面PDC,又PC平面PDC,∴AD⊥PC;
(2)由(1)知,AD⊥平面PCD,以点D为原点O建立空间直角坐标系,如图:
P在平面yDz内,在中,,利用余弦定理可得,所以可以得到P到y轴距离为,到z轴距离为1,所以P(0,-1,),
D(0,0,0),A(2,0,0),B(2,2,0),
所以,
易知是平面PCD的一个法向量,
设平面PAB的一个法向量为,
则,取z=2,则x=,y=0,所以,
则.
记两个平面的夹角为,则;
(3)存在,如上图可知,C(0,2,0),所以,
因为点Q在平面xDy内,可设Q(m,s,0),则,
由题意可知,,
所以,
又Q在平面xDy平面内,以点D为圆心,半径为2的一段圆弧的方程为,点Q在圆弧上,
所以有,
解得,
所以点Q的坐标为,故存在符合题意的点Q.
【解析】本题考查空间位置关系的证明,考查空间向量的应用,属于较难题.
(1)利用线面垂直的判定定理得到AD⊥平面PDC,即可证明;
(2)建立空间直角坐标系,利用空间向量求出二面角的大小的正弦值;
(3)设Q(m,s,0),利用空间向量的夹角公式得到,又Q在平面xOy平面内,以点D为圆心,半径为2的一段圆弧上,得到方程组求解即可判断是否存在.
15.【答案】解:证明:取的中点,连接,
因为为的中点, 且,
又为的中点,为的中点,所以 且,
故A 且,
所以四边形为平行四边形,
所以 ,
又平面,平面,
所以 平面;
以为原点,,,所在直线分别为轴轴轴,建立空间直角坐标系,
则,,,
易知平面的一个法向量为.
假设满足条件的点存在,令,
则,.
设平面的一个法向量是,
则,即
令,得,,所以
由题意得,,
解得,
故点不在线段上
【解析】本题考查线面平行的判定,考查利用空间向量求二面角的余弦值,考查推理论证能力、运算求解能力、空间想象能力,属于中档题.
根据题意结合三角形的中位线,平行四边形以及线面平行的判定定理即可求解;
以为原点,为轴,为轴,为轴建立空间直角坐标系,设,利用向量法表示出平面与平面所成的二面角为时的余弦值,解方程即可求解.
16.【答案】解:证明:若选,则,,,,
,且,平面,平面,平面,
若选,则,,,≌,,,
,,,且,平面,平面,平面,
若选,则,,,平面平面,平面平面,平面,
平面,平面,.
,, ,,平面,平面
又,,,两两垂直,如图,以为原点,
分别以,,的方向为,,轴的正方向,建立空间直角坐标系,
则,,,,
由于,可知,
,,
设为平面的法向量,
则即 取,则,,故可取,
易知为平面的一个法向量.
,
设二面角的平面角为,由图可得为锐角,
.
【解析】本题考查线线垂直,空间向量求二面角,属于中档题.
选条件证明平面,即可证明;
建立空间直角坐标系,求平面的一个法向量,为平面的一个法向量,利用空间向量法求解即可.
第1页,共1页
